Файл: Тема 3.doc

Абсолютная плотность распределения - это частота, приходящаяся на единицу длины интервала, т.е, аотносительная плотность распределения - частость, приходящаяся на единицу длины интервала, т.е..

Для различных целей бывает уместным осуществлять еще одно преобразование ряда распределения, заключающееся в построении ряда накопленных частот (кумулятивного ряда). Этот ряд показывает число случаев ниже или выше определенного уровня. Отсюда и возникают два варианта в построении ряда накопленных частот: один показывает число случаев, менее определенного значения варьирующего признака, а другой - число случаев, превышающее определенное значение варьирующего признака.

Аналогично определяются накопленные частости (последовательным суммированием частостей всех вариантов или интервалов). Накопленная частость показывает долю членов совокупности, у которых интересующий нас признак меньше данного значения.

Таблица 3.3
Распределение действующих кредитных организаций по величине зарегистрированного уставного капитала в России (по состоянию на 01.07.2001 г.)
№ п/п	Группы кредитных организаций по уставному капиталу, млн. руб.	Ширина интервала, млн. руб.	Число кредитных организаций	Плотность распределения
	А	1	2	3 (гр.2 : гр.1)
1	До 3	2	150	75
2	3-10	7	254	36,3
3	10-30	20	316	15,8
4	30-60	30	256	8,5
5	60-150	90	144	1,6
6	150-300	150	90	0,6
7	300-600	300	112	0,37
	Итого	-	1322	-

---

Графическое изображение рядов распределения. Графическое изображение облегчает анализ ряда распределения и позволяет судить о форме распределений единиц совокупности по значениям группировочного признака.

Для изображения вариационных рядов применяются линейные иплоскостные диаграммы, построенные в прямоугольной системе координат: полигон, гистограмма, огива, кумулята и кривая Лоренца.

Полигон используется при изображении дискретных вариационных рядов. Он представляет собой замкнутый многоугольник, абсциссами вершин которого являются значения варьирующего признака, а ординатами - соответствующие им частоты или частости.

Для примера рассмотрим построение полигона распределения по данным табл. 3.1. Отложив в выбранном масштабе число детей по оси абсцисс (), а соответствующее им число семей по оси ординат (), получаем совокупность точек. Соединим эти точки последовательно отрезками прямой, а из первой и последней точки опустим перпендикуляры на ось, в результате получим замкнутую фигуру в виде многоугольника (рис. 3.3).

Гистограмма (гр.histos- ткань, строение) применяется для изображения интервального вариационного ряда, который представляют столбики с основаниями, равными ширине интервалов, и высотой, соответствующей частоте. По сути гистограмма является одной из разновидностей столбиковых диаграмм.

Изобразим графически интервальный вариационный ряд распределения, приведенный в табл. 3.2 (рис. 3.4).

Гистограмма может быть преобразована в полигон распределения, если найти середины сторон прямоугольников и затем эти точки соединить прямыми линиями. Полученный полигон распределения изображен на рис.3.4 пунктирной линией.

При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах.

Для графического изображения вариационных рядов может также использоваться кумулятивная кривая. При помощи кумуляты изображается ряд накопленных частот.

---

При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.

Используя данные накопленного ряда (графа 2 табл. 3.2), построим кумуляту распределения (рис.3.5).

Изображение вариационного ряда в виде кумуляты особенно эффективно для вариационных рядов, частоты которых выражены в долях или процентах к сумме частот ряда.

Если в прямоугольной системе координат построим точки, ординаты которых - варианты, а абсциссы - накопленные частоты (или частости), а затем соединим их отрезки прямой, то получим ломаную линию, которая называется огивой. Огива распределения семей по размеру жилой площади, приходящейся на одного человека, приведена на рис.3.6.

Разновидностью кумулятивной кривой является график-кривая Лоренца. График используется для характеристики процессов концентрации, дифференциации, специализации и т.д.

Широкое применение компьютеров в практической работе экономиста облегчает построение рядов распределения, как и их графическое представление. Особо в этой связи следует отметить использование стандартизованных процедур определения величины интервала ряда распределения.

---

3.6 Сравнимость статистических группировок

Группировки, построенные за один и тот же период времени, но для разных регионов или, наоборот, для одного региона, но за два разных периода времени, могут оказаться несопоставимыми из-за различного числа выделенных групп или неодинаковости границ интервалов. Для того чтобы привести такие группировки к сопоставимому виду (это позволяет провести их сравнительный анализ), используется метод вторичной группировки. Суть метода состоит в перегруппировке единиц объекта без обращения к первичным данным.

Вторичная группировка - операция по образованию новых групп на основе ранее построенной группировки.

Применяют два способа образования новых групп. Первым, наиболее простым и распространенным способом является объединение первоначальных интервалов. Способ используется, когда нужен переход от мелких интервалов к более крупным интервалам, а также когда границы новых и старых интервалов совпадают. Второй способ получил названиедолевой перегруппировки; он состоит в образовании новых групп на основе закрепления за каждой группой определенной доли единиц совокупности. Этот способ употребляется, когда необходимо в ходе перегруппировки данных определить, какая часть (доля) единиц совокупности перейдет из старых групп в новые.

3.7 Метод группировок и многомерные классификации

Метод группировок позволяет получить общее представление о различных сторонах изучаемого объекта или процесса, выявить закономерности изменения основных показателей в совокупности, установить взаимосвязи и зависимости различных сторон изучаемых явлений, определить влияние факторов на изменение результативного признака.

Аналитические группировки, построенные по одному признаку, и сложные группировки позволяют установить связь и определить направление между результативными и 1-3 факторными признаками. Но часто этого бывает недостаточно, так как в действительности на изменение величины результативного признака оказывает влияние множество факторов, действующих в разных направлениях.

Для исследования таких многофакторных связей используются различные методы многомерной классификации, наибольшее распространение среди которых в практике экономико-статистического анализа социально-экономических явлений и процессов получили следующие, представленные на рис. 3.7.

---

В данной теме остановимся подробнее на раскрытии сущности алгоритма реализации и возможностей экономической интерпретации выходных параметров метода многомерной группировки - метода многомерных средних.

Целью таких группировок является разбиение совокупности социально-экономических явлений на качественно однородные группы по большому числу признаков одновременно и определение на их основе связи и влияния факторных признаков на результативный.

В основу построения многомерной группировки положен принцип перехода от величин, имеющих определенную размерность, к безразмерным относительным величинам,

Сущность и этапы реализации метода

1. Все значения (абсолютные) результативного признака заменяются отношением вида:

(3.5)

где - эмпирические значения результативного признака;

- средний уровень результативного признака.

2. Все значения (абсолютные) факторных признаков 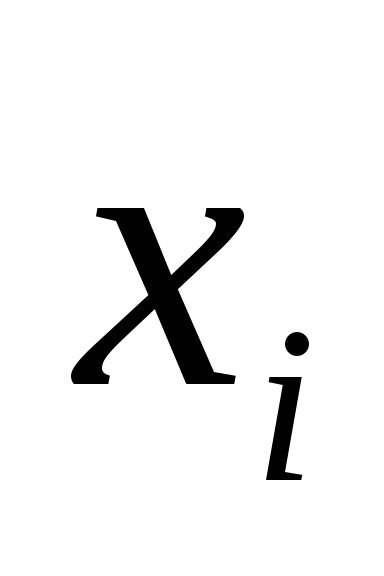заменяются отношениями:

(3.6)

Где - средний уровень-го факторного признака.

3. В результате такой замены (п. 1 и 2) матрица эмпирических абсолютных значений признаков и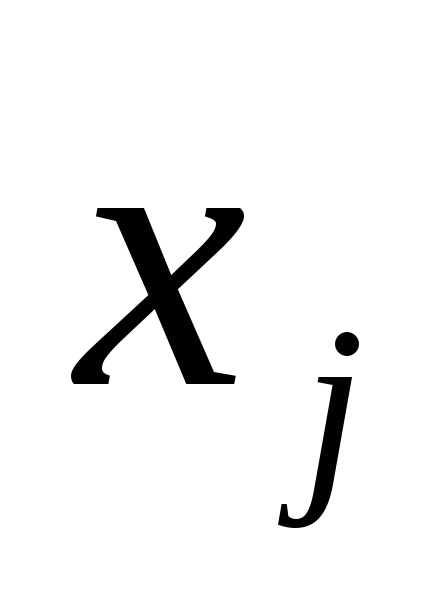 заменяется матрицей относительных величин и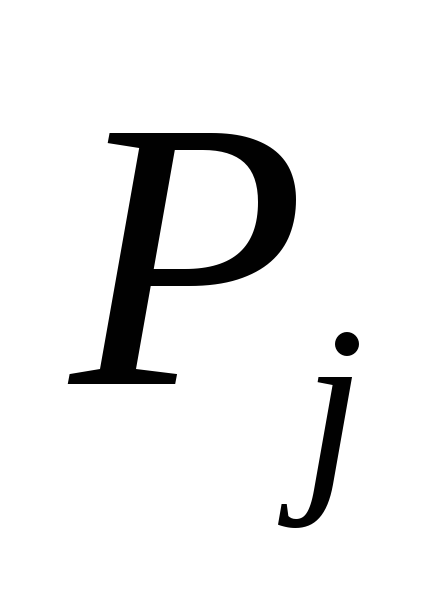следующего вида (табл. 3.4).

Таблица 3.4
Матрица относительных величин
№ п/п	Результативный признак	Факторные признаки
1
2
3
п

---