Файл: Тема 5.doc

Наглядность данной диаграммы достигается сравнением высоты столбиков.

Размещение столбиков в поле графика может быть различным:

• на одинаковом расстоянии друг от друга (рис. 5.7);

• вплотную друг к другу (рис. 5.8);

• в частичном наложении друг на друга (рис. 5.9).

Столбиковые диаграммы целесообразно применять для сравнения нескольких показателей. На рис. 5.10 посредством столбиковой диаграммы показана динамика удельного веса отдельных источников финансирования инвестиций в основной капитал за 1998-2000 годы. На этой диаграмме столбики располагаются вплотную по группам объектов. Масштаб принят такой, что каждым 5% соответствует отрезок на оси ординат 1 см. На диаграмме сделаны необходимые надписи и условные обозначения.

Разновидность столбиковых диаграмм составляют так называемые ленточные, илиполосовые, диаграммы. Их отличие состоит в том, что масштабная шкала расположена по горизонтали сверху или снизу и она определяет величину полос по длине. В качестве примера приведем полосовую диаграмму сравнения, характеризующую динамику выдачи кредитов коммерческими банками России.

Для построения данной диаграммы на поле графика отложим полосы, длина которых соответствует значениям изображаемых данных на масштабной шкале (рис. 5.11).

Из диаграммы следует, что среди выдачи кредитов коммерческими банками наибольшая их сумма приходится на 1 января 1999 г.

Столбиковые и полосовые диаграммы хорошо подходят для характеристики состава совокупности. Структура состава совокупности лучше воспринимается не в абсолютных, а в относительных величинах. При таких данных все столбики (полосы) в диаграмме имеют одинаковую высоту и соответствуют 100%. Каждый столбик разбивается на части пропорционально удельному весу отдельных частей во всей совокупности. Примером такой диаграммы является рис. 5.12, характеризующий структуру продаж по регионам за период с 1990 по 2000 г.

Таким образом, область применения столбиковых и полосовых диаграмм одинакова, так как идентичны правила их построения. Одномерность изображаемых статистических показателей и их одномасштабность для различных столбиков и полос требуют выполнения единственного положения: соблюдения соразмерности (столбиков - по высоте, полос - по длине) и пропорциональности изображаемым величинам.

---

Для выполнения этого требования необходимо соблюдать следующие условия:

• шкала, по которой устанавливается размер столбика (полосы), должна начинаться с нуля;

• шкала должна быть непрерывной, т.е. охватывать все числа данного статистического ряда;

• разрыв шкалы и соответственно столбиков (полос) не допускается. Невыполнение указанных правил приводит к искаженному графическому представлению анализируемого статистического материала.

Разновидностью столбиковых (ленточных) диаграмм являются направленные диаграммы. Они отличаются от обычных двусторонним расположением столбиков или полос и имеют начало отсчета по масштабу в середине. Обычно такие диаграммы применяются для изображения величин противоположного качественного значения. Сравнение между собой столбиков (полос), направленных в разные стороны, менее эффективно, чем расположенных рядом в одном направлении. Несмотря на это, анализ направленных диаграмм позволяет делать достаточно содержательные выводы, так как особое расположение придает графику яркое изображение. Кгруппе двусторонних относятся диаграммы числовых отклонений. В них полосы направлены в обе стороны от вертикальной нулевой линии: вправо - для прироста; влево - для уменьшения. С помощью таких диаграмм удобно изображать отклонения от плана или некоторого уровня, принятого за базу сравнения. Важным достоинством рассматриваемых диаграмм является возможность видеть размах колебаний изучаемого статистического признака, что само по себе имеет большое значение для экономического анализа. Данные диаграммы широко применяются в демографии (рис. 5.13).

Для простого сравнения независимых друг от друга показателей могут также использоваться диаграммы, принцип построения которых состоит в том, что сравниваемые величины изображаются в виде правильных геометрических фигур, которые строятся так, чтобы площади их относились между собой как количества, этими фигурами изображаемые. Иными словами, эти диаграммы величину изображаемого явления выражают размером своей площади.

Для создания диаграмм такого типа используют разнообразные геометрические фигуры - квадраты, круги, реже - прямоугольники. Для построения квадратных икруговых диаграмм необходимо сначала из статистических данных извлечь квадратные корни. Затем на базе полученных результатов определить сторону квадрата или радиус круга в соответствии с принятым масштабом.

---

Например, необходимо изобразить в виде квадрата или круга доходы от услуг связи населению России в 2000 г.: почтовая составила 4662 млн. руб., международная и междугородняя телефонная - 16714 млн. руб., городская и сельская телефонная - 14560 млн. руб.

Для построения квадратной диаграммы сначала извлечем квадратные корни из чисел: ;;.

Затем установим масштаб, например, примем 1 см - 30 млн. руб. Тогда сторона 1-го квадрата составит 4,3 см. (129,3 : 30); 2-го - 4,0 см. (120,7 : 30), 3-го - 2,3 см. (68,3 : 30) (рис. 5.14).

Круговая диаграмма строится аналогично квадратной с той разницей, что находим величину радиуса для каждого круга, т.е. при масштабе 1 см - 30 млн. руб. радиус 1-го круга будет равен - 2,3 см., 2-го - 4,0 см. и 3-го - 4,3 см. (рис.5.15).

Для правильного построения диаграмм квадраты или круги необходимо расположить на одинаковом расстоянии друг от друга, а в каждой фигуре указать числовое значение, которое она изображает, не приводя масштаба измерения.

К рассматриваемому виду диаграмм относится графическое изображение, полученное путем построения один в другом квадратов, кругов или прямоугольников с различной заштриховкой или закраской. Такие диаграммы также позволяют сравнивать между собой ряд исследуемых величин.

Прямоугольные диаграммы (не квадраты!) находят себе применение при графическом изображении, главным образом для двумасштабных сравнений: один масштаб для основания, другой - для высоты. Эти диаграммы называютсязнаками Варзара. Обычно они применяются в тех случаях, когда показатель является произведением двух других (например, сумма вкладов есть произведение числа вкладов на средний размер вкладов; численность населения является произведением плотности населения на территорию; валовой сбор есть произведение посевной площади на урожайность и т.д.). Такой показатель можно графически изобразить в виде сомножителей. Для этого поступают следующим образом: один сомножитель принимают за основание, другой - за высоту. Затем устанавливают масштабы: один для основания, другой для высоты. Далее, располагая значением показателя основания и высоты, строят прямоугольники. Покажем этот способ на примере данных по сбору плодов и ягод в одном из регионов России, в котором при посевной площади 936 тыс. га урожайность составила 23,6 ц./га. (рис. 5.16). В нашем случае в основание прямоугольника положена урожайность плодов и ягод, высота - посевная площадь, а площадью прямоугольника является валовой сбор плодов и ягод (тыс. т.).

---

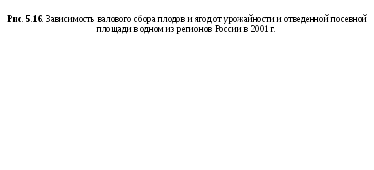
Весьма выразителен и хорошо воспринимается способ построения диаграмм сравнения в виде фигур-знаков. В этом случае статистические показатели изображаются не геометрическими фигурами, а символами или знаками, воспроизводящими в какой-то степени внешний образ статистических данных. Достоинство такого способа графического изображения заключается в высокой степени наглядности, в получении подобного отображения, отражающего содержание сравниваемых совокупностей.

Важнейший признак любой диаграммы - масштаб. Поэтому, чтобы правильно построить фигурную диаграмму, необходимо определитьединицу счета. В качестве последней принимается отдельная фигура (символ), которой условно присваивается конкретное численное значение. А исследуемая статистическая величина изображается отдельным количеством одинаковых по размеру фигур, последовательно располагающихся на рисунке. Однако в большинстве случаев не удается изобразить статистический показатель целым количеством фигур. Последнюю из них приходится делить на части, так как по масштабу один знак является слишком крупной единицей измерения. Обычно эта часть определяется на глаз. Сложность точного ее определения является недостатком фигурных диаграмм. Однако если большая точность представления статистических данных не преследуется, то результаты получаются вполне удовлетворительными.

Пример. Рассмотрим построение фигурной диаграммы по данным закупок крупного рогатого скота в одном из регионов России в хозяйствах всех категорий.

В 1999 г. - 6,5 млн. т, в 2000 г. - 4,4 млн. т, в 2001 г. - 33 млн. т.

Примем условно за один знак 1,1 млн. т закупок крупного рогатого скота. Разделим приведенные показатели на 1,1 и получим число фигур: для 1 999 г. - 6; для 2000 г. - 4; для 2001 г. - 3. Построим диаграмму (рис.5.17).

---

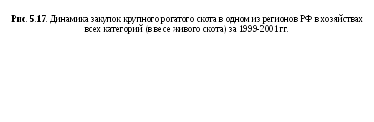
5.4 Структурные диаграммы

Основное назначение структурных диаграмм заключается в наглядной иллюстрации структуры какого-либо явления, характеристике удельных весов отдельных частей целого, выявлении структурных сдвигов.

В качестве графического образа для изображения структуры совокупностей применяются прямоугольники - для построения столбиковых и полосовых диаграмм и круги - для построения секторных диаграмм.

Круг часто используется в качестве геометрической формы при построении диаграммы. Следует различать два вида применения круга. В одном случае сравниваются площади кругов друг с другом. Такого рода диаграмма называется круговой (см. рис. 5.15). В другом случае круг используется для сравнения площади отдельных секторов друг с другом. Такая диаграмма именуетсясекторной.

Идея целого очень хорошо и наглядно выражается кругом, который представляет всю совокупность. Удельный вес каждой части совокупности в секторной диаграмме характеризуется величиной центрального угла (угол между радиусами круга). Сумма всех углов круга, равная 360°, приравнивается к 100%, а следовательно, 1% принимается равным 3,6°. Графическое изображение структуры с помощью столбиковой диаграммы приведено ранее (см. рис. 5.12). Построение полосовой секторной диаграммы покажем на данных, характеризующих динамику структуры денежных доходов населения в России (табл. 5.2).

Таблица 5.2
Структура денежных доходов населения России, %
Год	Оплата труда	Социальные трансферты	Доходы от собственности	Доходы от предпринимательской деятельности	Другие доходы
1992	73,6	14,3	1,0	8,4	2,7
1999	64,2	13,3	7,3	14,3	0,9

---