ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.08.2024
Просмотров: 81
Скачиваний: 0
Полулогарифмической сеткой называется сетка, в которой на одной оси нанесен линейный масштаб, а на другой - логарифмический. В данном случае логарифмический масштаб наносится на ось ординат, а на оси абсцисс располагают равномерную шкалу для отсчета времени по принятым интервалам (годам, кварталам, месяцам, дням и пр.). Техника построения логарифмической шкалы следующая (рис. 5.23). Необходимо найти логарифмы исходных чисел, начертить ординату и разделить ее на несколько равных частей. Затем нанести на ординату (или равную ей параллельную линию) отрезки, пропорциональные абсолютным приростам этих логарифмов. Далее записать соответствующие логарифмы чисел и их антилогарифмы, например (0,000; 0,3010; 0,4771; 0,6021; ...; 1,000, что дает 1, 2, 3, 4, ..., 10). Полученные антилогарифмы окончательно дают вид искомой шкалы на ординате.

Пример. Построим диаграмму на полулогарифмической сетке. Допустим, что надо изобразить на графике динамику производства электроэнергии в регионе за 1995 - 2001 гг., за эти годы оно выросло в 9,1 раза. С этой целью находим логарифмы для каждого уровня ряда (табл. 5.5).
|
Таблица 5.5 |
|||||
|
Динамика производства электроэнергии в регионе за 1995-2001 гг. (млрд. кВт •ч)* |
|||||
|
Год |
|
|
Год |
|
|
|
1995 |
170 |
2,23 |
1999 |
1039 |
3,02 |
|
1996 |
292 |
2,46 |
200 |
1294 |
3,11 |
|
1997 |
507 |
2,70 |
2001 |
1544 |
3,19 |
|
1998 |
741 |
2,84 |
|
|
|
|
* Цифры условные. |
|||||
Определив минимальное и максимальное значение логарифмов производства электроэнергии, построим масштаб с таким расчетом, чтобы все данные разместились на графике.
Учитывая масштаб, находим соответствующие точки, которые соединим прямыми линиями, в результате получаем график (рис. 5.24) с использованием логарифмического масштаба на оси ординат. Он называется диаграммой на полулогарифмической сетке. Полной логарифмической диаграммой он станет в том случае, если по оси абсцисс будет построен логарифмический масштаб. В рядах динамики это никогда не применяется, так как логарифмирование времени лишено всякого смысла.

Применяя логарифмический масштаб, можно без всяких вычислений характеризовать динамику уровня. Если кривая на логарифмическом масштабе несколько отклонена от прямой и становится вогнутой к оси абсцисс, значит, имеет место падение темпов; когда кривая в своем течении приближается к прямой - стабильность темпов; если она отклоняется от прямой в сторону, выпуклую к оси абсцисс, изучаемое явление имеет тенденцию к росту с увеличивающимися темпами.
Динамику изображают и радиальные диаграммы, строящиеся в полярных координатах. Радиальные диаграммы преследуют цель наглядного изображения определенного ритмического движения во времени. Чаще всего эти диаграммы применяются для иллюстрации сезонных колебаний. Радиальные диаграммы разделяются на замкнутые и спиральные. По технике построения радиальные диаграммы отличаются друг от друга в зависимости от того, что взято в качестве пункта отсчета - центр круга или окружность.
Замкнутые диаграммы отражают внутригодичный цикл динамики какого-либо одного года.Спиральные диаграммы показывают внутригодичный цикл динамики за ряд лет.
Построение замкнутых диаграмм сводится
к следующему: вычерчивается круг,
среднемесячный показатель приравнивается
к радиусу этого круга. Затем весь круг
делится на 12 радиусов, которые на графике
приводятся в виде тонких линий. Каждый
радиус обозначает месяц, причем
расположение месяцев аналогично
циферблату часов: январь — в том месте,
где на часах 1, февраль - 2 и т.д. На каждом
радиусе делается отметка в определенном
месте согласно масштабу исходя из данных
за соответствующий месяц. Если данные
превышают среднемесячный уровень,
отметка делается за пределами окружности
на продолжении радиуса. Затем отметки
различных месяцев соединяются отрезками.
В приведенном примере (рис. 5.25)
![]() тыс. т., длина радиуса - 3,0 см. Следовательно,
1 см. = 44,8 : 3,0
тыс. т., длина радиуса - 3,0 см. Следовательно,
1 см. = 44,8 : 3,0![]() 15 тыс. т. Данная замкнутая диаграмма
наглядно показывает, что производство
мяса подвергнуто сезонным колебаниям.
Минимум производства мяса приходится
на апрель, май, затем наблюдается
медленное его повышение к августу,
резкий подъем в сентябре, октябре и
опять спад в декабре, январе. Если же в
качестве базы для отсчета взять не центр
круга, а окружность, то диаграммы
называются спиральными.
15 тыс. т. Данная замкнутая диаграмма
наглядно показывает, что производство
мяса подвергнуто сезонным колебаниям.
Минимум производства мяса приходится
на апрель, май, затем наблюдается
медленное его повышение к августу,
резкий подъем в сентябре, октябре и
опять спад в декабре, январе. Если же в
качестве базы для отсчета взять не центр
круга, а окружность, то диаграммы
называются спиральными.
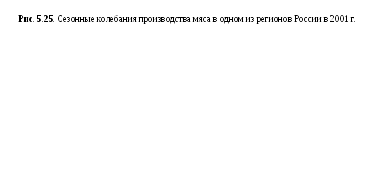
Построение спиральных диаграмм отличается от замкнутых тем, что в них декабрь одного года соединяется не с январем данного же года, а с январем следующего года. Это дает возможность изобразить весь ряд динамики в виде спирали. Особенно наглядна такая диаграмма, когда наряду с сезонными изменениями происходит неуклонный рост из года в год (рис. 5.26).
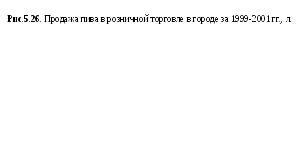
Среди различных видов графиков особое место занимает кривая, именуемая моделью Лоренца, или кривой Лоренца. Данная кривая дает возможность графически изобразить уровень концентрации явления. Пример построения кривой Лоренца описан в главе 11.
5.6 Статистические карты
Статистические карты представляют собой вид графических изображений статистических данных на схематической географической карте и характеризуют уровень или степень распространения того или иного явления на определенной территории.
Средствами изображения территориального размещения являются штриховка, фоновая раскраска или геометрические фигуры. Различают картограммы и картодиаграммы.
Картограмма - это схематическая географическая карта, на которой штриховкой различной густоты, точками или окраской определенной степени насыщенности показывается сравнительная интенсивность какого-либо показателя в пределах каждой единицы нанесенного на карту территориального деления (например, плотность населения по областям или республикам, распределение районов по урожайности зерновых культур и т.п.). Картограммы делятся на фоновые и точечные.
Картограмма фоновая - вид картограммы, на которой штриховкой различной густоты или окраской определенной степени насыщенности показывают интенсивность какого-либо показателя в пределах территориальной единицы.
Картограмма точечная - вид картограммы, где уровень выбранного явления изображается с помощью точек. Точка изображает одну единицу совокупности или некоторое их количество, показывая на географической карте плотность или частоту проявления определенного признака.
Фоновые картограммы, как правило, используются для изображения средних или относительных показателей, точечные - для объемных (количественных) показателей (численность населения, поголовье скота и т.д.).
Пример.Рассмотрим построение картограммы, используя данные табл. 5.6.
|
Таблица 5.6 |
||||||||
|
Плотность населения восьми районов области* |
||||||||
|
№ района |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Плотность населения на 1000 км.2, тыс. чел. |
3,0 |
4,0 |
11,0 |
14,0 |
17,0 |
13,0 |
11,0 |
3,0 |
|
* Цифры условные. |
||||||||
Прежде чем приступить к построению картограммы, необходимо разбить районы на группы по плотности населения, а затем установить для каждой определенную окраску или штриховку.
Согласно данным табл. 5.6 все районы по плотности населения можно разбить на три группы:
1) до 4 тыс. чел.;
2) от 4 до 12 тыс. чел.;
3) от 12 до 17 тыс. чел.
Тогда к 1-й группе относятся районы № 1, 8; ко 2-й - № 2, 3, 7; к 3-й - № 4, 5, 6. Если принять для каждой группы районов окраску различной насыщенности, то на фоновой картограмме хорошо видно, как располагаются на территории области отдельные районы по плотности населения (рис. 5.27). Другим примером фоновой картограммы является рис. 5.28.


Вторую большую группу статистических карт составляют картодиаграммы, представляющие собой сочетание диаграмм с географической картой. В качестве изобразительных знаков в картодиаграммах используются диаграммные фигуры (столбики, квадраты, круги, фигуры, полосы), которые размещаются на контуре географической карты. Картодиаграммы дают возможность географически отразить более сложные статистико-географические построения, чем картограммы.
Среди картодиаграмм следует выделить картодиаграммы простого сравнения, графики пространственных перемещений, изолиний.
На картодиаграмме простого сравнения в отличие от обычной диаграммы диаграммные фигуры, изображающие величины исследуемого показателя, расположены не в ряд, как на обычной диаграмме, а разносятся по всей карте в соответствии с тем районом, областью или страной, которые они представляют.
Элементы простейшей картодиаграммы можно обнаружить на политической карте, где города отличаются различными геометрическими фигурами в зависимости от числа жителей.
В качестве примера картодиаграммы возьмем изображение валового сбора зерна Центрального района России (рис. 5.29).
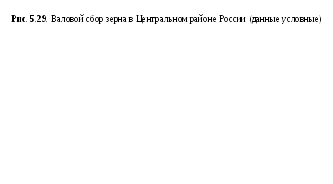
Изолинии (греч. 1308 - равный, одинаковый, подобный) - это линии равного значения какой-либо величины в ее распространении на поверхности, в частности на географической карте или графике. Изолиния отражает непрерывное изменение исследуемой величины в зависимости от двух других переменных и применяется при картографировании природных и социально-экономических явлений. Изолинии используются для получения количественных характеристик исследуемых величин и для анализа корреляционных связей между ними.