11

Проблема изучения взаимосвязей экономических показателей явля­ется одной из важнейших в экономическом анализе. Эконометрика - наука, исследующая количественные закономерно­сти и взаимосвязи в экономике при помощи методов математической ста­тистики. Название «эконометрика» введено в 1926 г. норвежским экономи­стом и статистиком Р. Фришем. Буквальный перевод этого понятия - «из­мерения в экономике».

Исследуя природу, общество, экономику, необходимо считаться со взаимосвязью наблюдаемых процессов и явлений. При этом полнота описания так или иначе определяется количест­венными характеристиками причинно-следственных связей между ними. Оценка наиболее существенных из них, а также воздействия одних факторов на другие является одной из основных задач статистики.

По направлению связи бывают прямыми, когда зависимая переменная растет с увеличением факторного признака, и обратными, при которых рост последнего сопровождается уменьшением функции. Такие связи также можно назвать соответственно положительными и отрицательными.

Относительно своей аналитической формы связи бывают линейными и нелинейными. В первом случае между признаками в среднем проявляются линейные соотношения. Нелинейная взаимосвязь выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно.

Существует еще одна достаточно важная характеристика связей с точки зрения взаимодействующих факторов. Если характеризуется связь двух признаков, то ее принято называть парной, если изучаются более чем две переменные, — множественной.

По силе различаются слабые и сильные связи. Эта формальная характеристика выражается конкретными величинами и интерпретируется в соответствии с общепринятыми критериями силы связи для конкретных показателей.

В наиболее общем виде задача эконометрики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. . Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая — регрессионный анализ. Задачи собственно корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов, оказывающих наибольшее влияние на результативный признак.

---

Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, исполь­зования уравнения для оценки неизвестных значений зависимой переменной.

Решение названных задач опирается на соответствующие приемы, алгоритмы, показатели, применение которых дает основание говорить о статистическом изучении взаимосвязей и использовать математический аппарат статистики.

Основная идея эконометрики - взаимосвязь между экономическими переменными. Обычно рассматриваются переменные, величина которых формируется под воздействием некоторых факторов. В случае наличия взаимосвязи между переменными, одна из них является зависимой или объясняемой переменной (результирующим показателем), и другие - объясняющими переменными. Установив характер взаимосвязи можно получить ожидаемое значение зависимой переменной при заданных значениях объясняющих переменных, то есть построить эконометрическую модель. Следует подчеркнуть, что конкретные, наблюдаемые значения зависимой переменной в большинстве случаев зависят также от случайных явлений, таких как инфраструктура рынка, характер продавца, наличие конкретной суммы и т.д.

Поэтому, как правило, в каждое соотношение приходится вводить не­сколько объясняющих переменных и остаточную случайную составляю­щую, отражающую влияние на результирующий показатель всех неучтен­ных факторов.

Участвующая в каждом из этих соотношений случайная состав­ляющая, отражающая влияние на результирующий показатель всех неуч­тенных факторов, обуславливает стохастический (вероятностный) характер зависимости: даже фиксировав значения объясняющих переменных нельзя ожидать однозначно, каким будет значение объясняемой переменной.

Таким образом, общим моментом для любой эконометрической модели является разбиение зависимой переменной на две части – объясненную и случайную:

Y = f(X) + l

Задача моделирования состоит в том, чтобы на основании экспериментальных данных определить объясненную часть и, рассматривая случайную составляющую как случайную величину, получить (возможно после некоторых предположений) оценки параметров ее распределения.

---

Наиболее распространенной формализацией стохастической (случайной, вероятностной) зави­симости между результирующим показателем у и объясняющими пере­менными х₁ , х₂ , х_n . в экономике является аддитивная (получаемая путем сложения) линейная форма:

у = а₀ + а₁х₁+а₂х₂ +.... +а_nx_n + l_t (1.1)

где а₀, а₁,… а_n - некоторые параметры (обычно неизвестные до проведе­ния соответствующего статического анализа), + l_t- случайная составляющая, характеризующая разницу между модельным и наблюденным значениями анализируемой результирующей переменной, обнаруженную в t-м измерении. Под модельным (ожидаемым) значением результирующей переменной понимаем ее значение, восстановленное по заданным величинам объяс­няющих переменных при условии, что коэффициенты а₀, а₁,.... ,а_п нам известны:

= а₀ + a₁х₁+a₂x₂ +.... + а_nх_n

Случайную составляющую l можно считать случайной ошибкой прогноза у по заданным значениям х₁,....,х_п. Обычно полагают, что сред­нее значение l_t при всех t равно нулю (l_t = 0).

Математическая модель - упрощенное, формализованное представление реальности (объекта, явления, процесса). Количест­во связей в модели зависит от условий, в которых она конструируется, от подробности объяснения, к которой стремится исследователь.

Все экономические модели имеют общие особенности:

- принимается, что модель улавливает главные характеристики изучаемого объекта;

- полагается, что на основе достигнутого с ее помощью понимания реальной системы удастся предсказать будущее движение экономических показателей.

Результирующая (зависимая) переменная у.

Она характеризует результат или эффективность функционирования эко­номической системы. Значения ее формируются в процессе и внутри функционирования этой системы под воздействием ряда других перемен­ных и факторов, часть из которых поддается регистрации, управлению и планированию (т.е. объясняющие переменные). В регрессионном анализе результирующая переменная играет роль функции, значение которой оп­ределяется значениями объясняющих переменных, выполняющих роль аргументов. По своей природе результирующая переменная всегда случай­на (стохастична).

---

Объясняющие переменные X.

Это - переменные, поддающиеся регистрации, описывающие условия функционирования реальной экономической системы. Они в значительной мере определяют значения результирующих переменных. Обычно, часть из них поддается регулированию и управлению. Значение этих перемен­ных могут задаваться вне анализируемой системы. Поэтому их называют экзогенными. В регрессионном анализе это аргументы результирующей функции у.

Уравнения регрессионной связи между у и X.

Математически уравнение регрессионной связи можно выразить следующим образом:

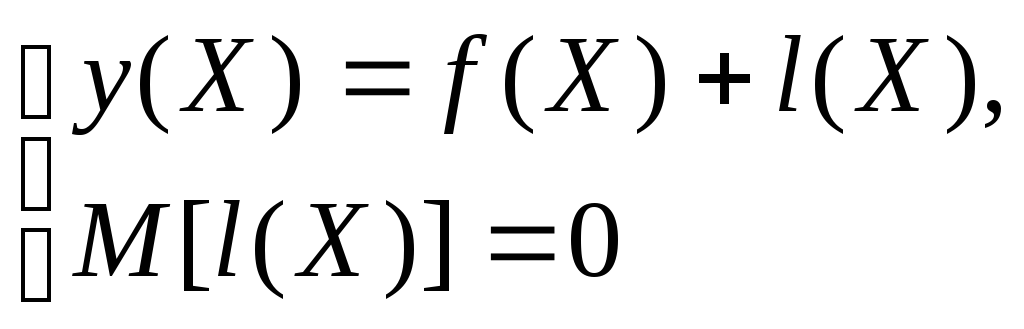
Здесь 1(Х) - «остаточная» составляющая («регрессионные остатки»), присутствие которой обусловлено как тем, что она отражает влияние на формирование значений у факторов, не учтенных в наборе объясняю­щих переменных X, так и тем, что она может включить в себя случайную погрешность в измерении значений у. Второе соотношение в системе означает равенство нулю математического ожидания остаточной составляющей.

Парная регрессия характеризует связь между двумя призна­ками: результативным и факторным. Аналитическая связь меж­ду ними описывается уравнениями:

1. прямой

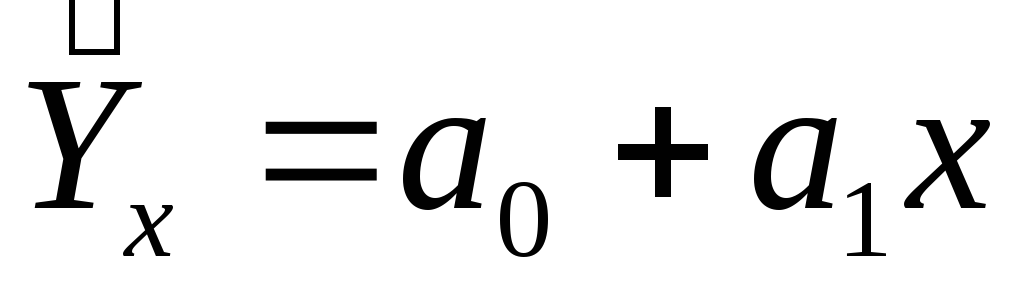
2. гиперболы

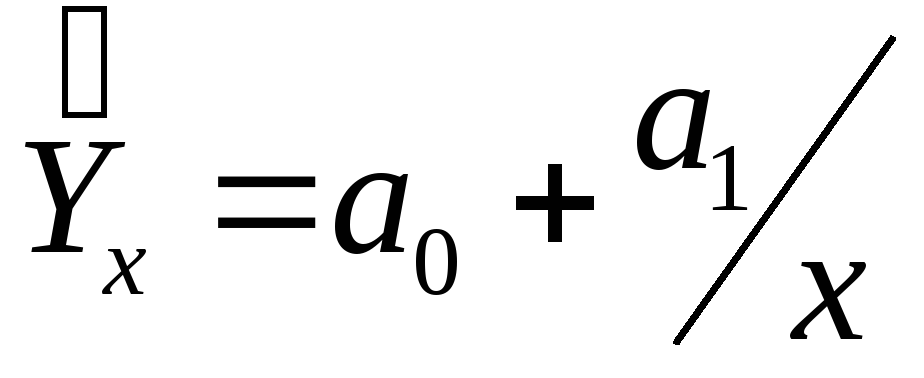
3. параболы

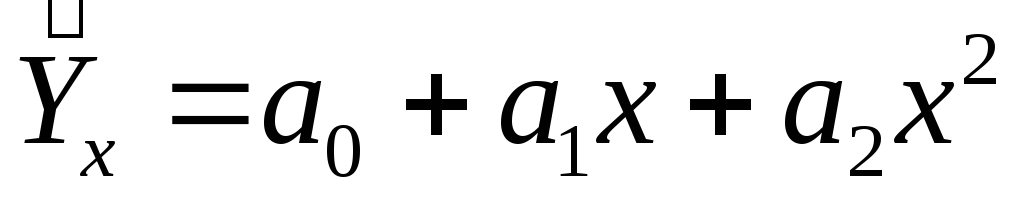
Определить тип уравнения можно, исследуя зависимость гра­фически. Однако существуют более общие указания, позволяю­щие выявить уравнение связи, не прибегая к графическому изоб­ражению. Если результативный и факторный признаки возраста­ют одинаково, примерно в арифметической прогрессии, то это свидетельствует о том, что связь между ними линейная, а при обратной связи - гиперболическая. Если факторный признак увеличивается в арифметической прогрессии, а результатив­ный - значительно быстрее, то используется параболическая, или степенная регрессия.

1. Рассмотрим парную линейную регрессию. пусть некоторый экономический процесс характеризуется статистическими данными, в которых представлены соответствующие друг другу выборки n вариантов двух дискретных случайных величин Y и X, записанные в таблице:

---

i	1	2	…	i	…	n
xi	x1	x2	…	xi	…	xn
yi	y1	y2	…	yi	…	yn

2. Наглядным изображением корреляционной таблицы служит корреляционное поле. Оно представляет собой график, где на оси абсцисс откладываются значения X, по оси ординат — Y, а точками показывается сочетание первичных наблюдений Х и Y. По расположению точек, их концентрации в определенном направлении можно судить о наличии связи.

Изобразим полученную зависимость графически точками координатной плоскости, то есть – корреляционное поле.

y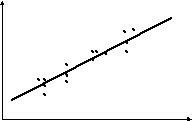

судя по рисунку, можно предположить, что между Х и Y существует корреляционная связь и зависимость Y от X может быть изображена в виде прямой линии, максимально приближенной к точкам корреляционного поля, уравнение которой будет:

Значение называется модельным (теоретическим, расчетным) значением результирующей переменной.

3. Для количественной оценки тесноты связи между переменными Y и X служит линейный коэффициент парной корреляции r_xy, вычисляемый по формуле:

---

Смотрите также файлы

• экзамен.docx

• Экзамен по Информатике.doc

• Эволюция звёзд.doc

• Эволюционная химия.doc

• шпоры.doc