, где

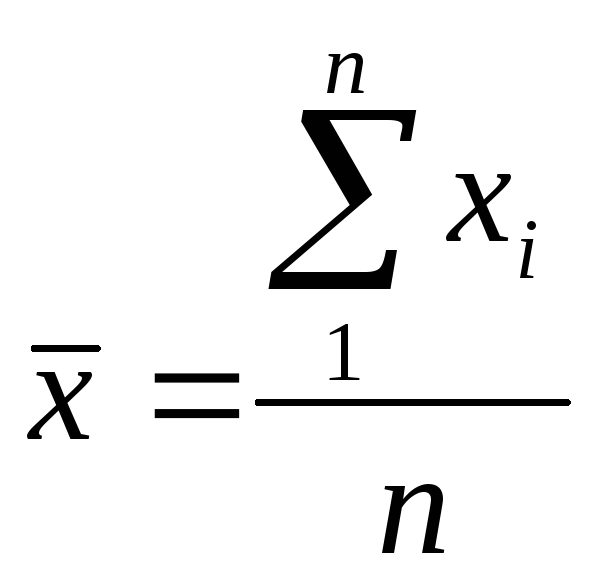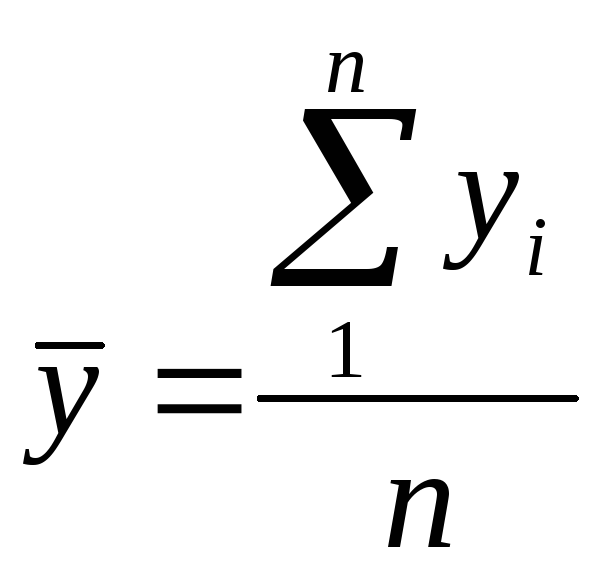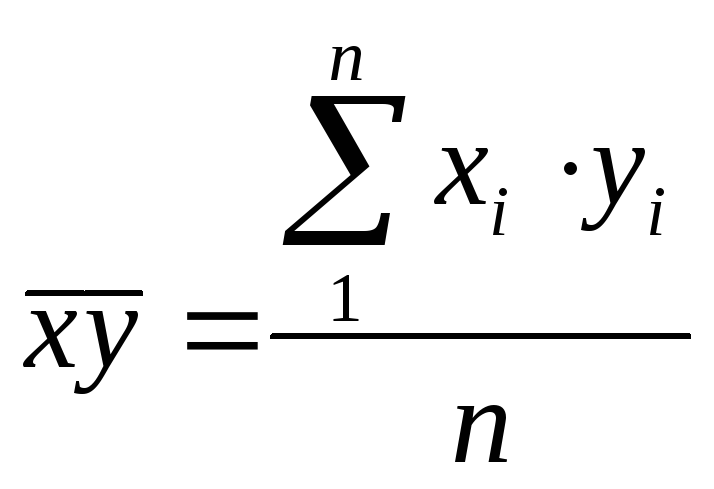, , – средние значения,

., – средние квадратичные отклонения,

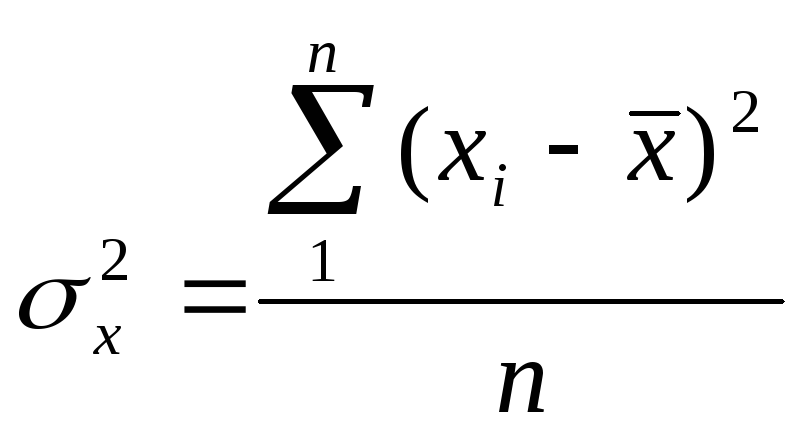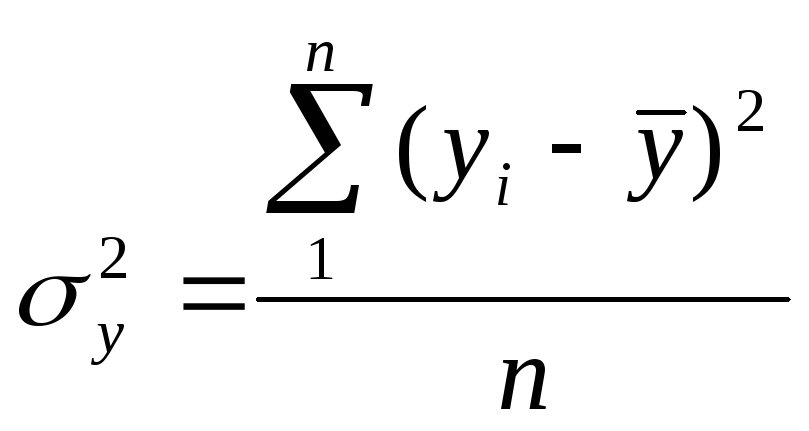, – дисперсия признаков,

В таблице приведены качественные оценки степени тесноты связи между переменными Y и X с помощью коэффициента корреляции.

Таблица. Теснота связи и величина коэффициента корреляции

Коэффициент корреляции	Теснота связи
± 1	Функциональная связь
от ± 0,91 до ± 1,00	Очень сильная
от± 0,81 до ± 0,90	Весьма сильная
от± 0,65 до ± 0,80	Сильная
от± 0,45 до ± 0,64	Умеренная
от± 0,25 до ± 0,44	Слабая
От 0 до ± 0,25	Очень слабая
0	Связи нет

---

4. Оценка параметров уравнений регрессии осуществляется методом наи­меньших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности.

Основной принцип метода наименьших квадратов применим для случая, когда две величины (два показателя) X и Y взаимосвязаны между собой, причем Y находится в некоторой зависимости от X. Следовательно, Y бу­дет зависимой, а X - независимой величинами.

Сущность метода наименьших квадратов заключается в нахож­дении параметров модели (а₀, а₁). Неизвестные параметры а₀ и a₁ линейного уравнения парной регрессии выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений у_i от расчетных значений , найденных по уравнению регрессии была минимальной:

Рассматриваем S в качестве функции параметров а₀, и а₁, и про­водим математические преобразования (дифференцирование). на основании необходимого условия экстремума функции двух переменных S=S(а₀,a₁) приравниваем к нулю ее частные производные и по­лучаем:

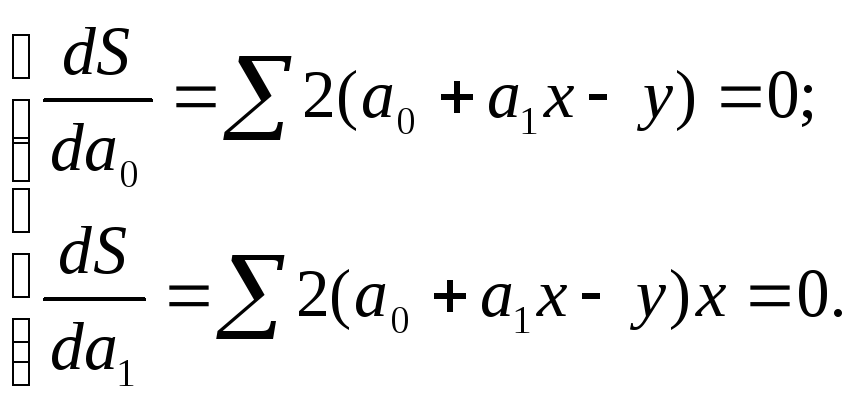
Откуда система нормальных уравнений для нахождения пара­метров линейной парной регрессии методом наименьших квад­ратов имеет следующий вид:

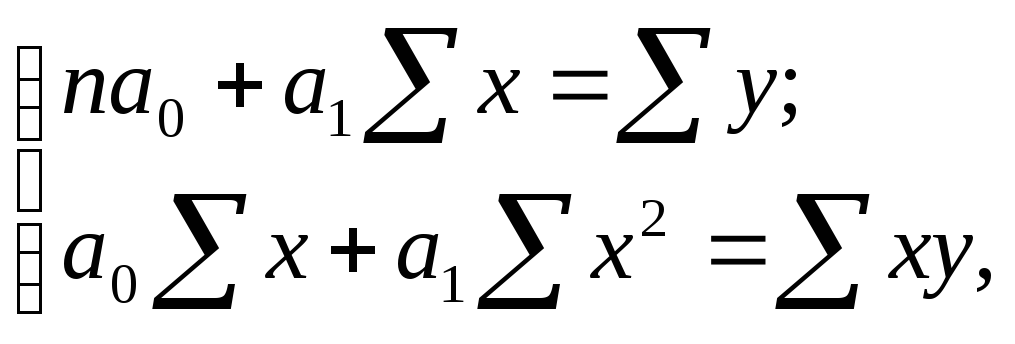
где n- объем исследуемой совокупности (число единиц наблюдений).

Коэффициент а₁ называется выборочным коэффициентом регрессии y по x и характеризует влияние, которое оказывает изменение X на Y. Он показывает на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу. Если а₁ > 0 , то связь – положительная, если а₁ < 0, то увеличение Х на единицу влечет за собой уменьшение Y в среднем на а_1.

---

Коэффициент a₀ – постоянная величина в уравнении регрессии, которую можно рассматривать как начальное значение Y, если в этом есть экономический смысл.

Решая систему найдем формулы для расчета коэффициентов a₀ и а₁ уравнения , а именно:

,

.

Качество полученной модели оценивается с помощью средней ошибки аппроксимации (приближения), которая показывает среднее отклонение расчетных значений от фактических и определяется по формуле:

, где

При Ā < 8 –10% качество модели считается весьма хорошим, а допустимый предел составляют значения в 12 – 15%.

При расчетах - исходные данные значений y, а - рассчитанные по формуле (т.е. по полученному уравнению регрессии). Причем одинаковый индекс указывает на то, что эти значения соответствуют одному и тому же значению х и находятся в одной строке.

Проверка адекватности всей модели производится на основе тестирования статистических гипотез.

Статистической гипотезой называется любое предположение о виде и параметре неизвестного закона распределения.

Проверяемую гипотезу обычно называют нулевой и обознача­ют H₀. Наряду с нулевой гипотезой H₀ рассматривают альтернативную, или конкурирующую, гипотезу Н₁, являющуюся логиче­ским отрицанием H₀. Нулевая и альтернативная гипотезы пред­ставляют собой две возможности выбора, осуществляемого в задачах проверки статистических гипотез.

Правило, по которому гипотеза h₀ отвергается или принимается, называется статистическим критерием или статистическим тестом.

Проверить значимость уравнения регрессии — значит уста­новить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

---

Проверка значимости уравнения регрессии производится на основе дисперсионного анализа, который применяется как вспомогательное средство для изучения качества регрессионной модели.

На практике F-тест - оценивание качества уравнения регрессии - состоит в проверке гипотезы H₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера. F_факт определяется из соотношения зна­чений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

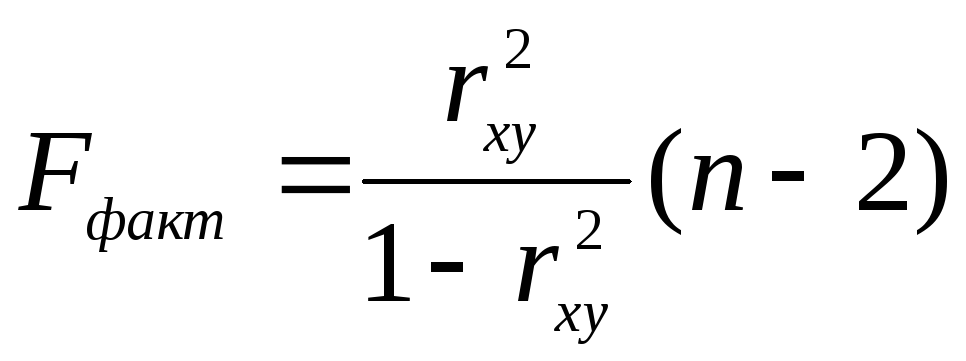
где п - число единиц совокупности; т - число параметров при переменных х.

F_табл - это максимально возможное значение критерия под влия­нием случайных факторов при данных степенях свободы и уровне значимости α. Уровень значимости α - вероятность отвергнуть пра­вильную гипотезу при условии, что она верна. Обычно α принимает­ся равной 0,05 или 0,01.

Если F_табл < F_факт, то H₀ - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F_табл > F_факт, то гипотеза Hо не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

. Для оценки статистической значимости коэффициентов регрессии рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Hо о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и кор­реляции с помощью t-критерия Стьюдента проводится путем сопос­тавления их значений с величиной случайной ошибки:

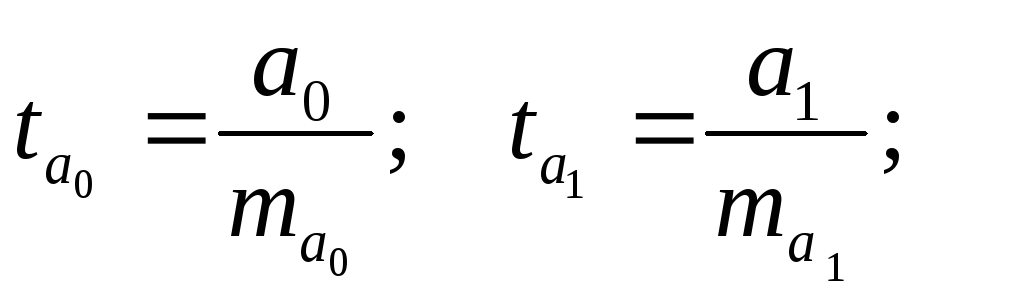
Сравнивая фактическое и критическое (табличное) значения t -статистики - t_табл и t_факт - принимаем или отвергаем гипотезу h₀.

Если t_табл < t_факт, то Н₀ отклоняется, т.е. a₀ , a₁ не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если t_табл > t_факт, то гипотеза h₀ не откло­няется и признается случайная природа формирования a₀ , a₁ и r_ху.

---

. Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации K_d, который показывает измерение степени тесноты статистической связи между у и X.

Для линейных регрессионных связей типа f(X)=a₀ +a₁x₁ +...+ а_nх_n (где а₀,а₁,....,а_n - числовые параметры) коэффициент детерминации совпадает с квадратом множественного коэффициента корреляции R²_y,_x,

Чем ближе R² к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к ли­нии регрессии. Если R²=1, то эмпирические точки (X_j, y_i) лежат на линии регрессии и между переменными Y и X су­ществует линейная функциональная зависимость. Если R² = 0, то вариация зависимой переменной полностью обусловлена воздейст­вием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс.

Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от сво­ей средней величины при изменении фактора х на 1% от своего среднего значения:

множественная (многофакторная) регрессия

Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) регрессии. При исследовании зависимостей методами множественной регрессии задача формулируется так же, как и при использовании парной регрессии, т.е. требуется определить аналитическое выражение связи между результативным признаком (У) и факторными признаками (х,, х₂, х₃, ... x_k), найти функцию: .

---

Смотрите также файлы

• экзамен.docx

• Экзамен по Информатике.doc

• Эволюция звёзд.doc

• Эволюционная химия.doc

• шпоры.doc