ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.08.2024
Просмотров: 25
Скачиваний: 0
|
23.Система дифференциальных уравнений
где
х1,х2 - искомые функции от t;
функции, называется системой линейных дифференциальных уравнений с постоянными коэффициентами второго порядка. Такую систему методом исключения можно привести к одному линейному урав-нению не выше второго порядка. |
16. Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.
|
|
|
|
|
|
58.Определение производной функции в точке. Геометрический и механический смысл производной. Производной
функции в точке
Функция
Значение
производной функции в точке
Скорость прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t – мех. Смысл производной. Геом.
Смысл : производная
|
59. Экономический смысл производной.
Пусть U=U(t) – функция, выражающая объем произведенной продукции за время t. Тогда
за
Если
использовать понятие
О.
эластичностью
ф-ии
|
60. Основные правила дифференцирования.
Дифф - процесс вычисления производной. Ф-ия называется дифференцируемой в точке если она имеет в этой точке конечную производную.
Теорема
1. Если U=U(x)
и V=V(x)
дифф. в точке x,
то ф-ия
|
62Логарифмическая произв-я.диффер-е ф-ии,заданных неявно В некоторых случаях для нахождения производной сложную функцию сначала логарифмируют: lnx+lny
= lnx lnx-lny
= ln lnxy = ylnx. Рассмотрим функцию заданную неявно F(x,y)=0: Для нахождения производной функции, заданной неявно, достаточно продифференцировать исходное уравнение по переменной х, считая у – функцией от х. Рассмотрим функцию заданную параметрически:
Вычисление
производной производится по формуле
|
|
64.производные и дифференциалы высших порядков 1.Пусть
Производной второго порядка называется производная от производной первого порядка. Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка.
2.
x=x(t) y=y(t)
ВОПРОС 69 Вторая производная. Если производная f ' ( x ) функции f ( x ) дифференцируема в точке ( x0 ), то её производная называется второй производной функции f ( x ) в точке ( x0 ), и обозначается f '' ( x0 ).
Функция
f (
x
) называется выпуклой
на интервале ( a,
b
), если её график на этом интервале
лежит ниже
касательной, проведенной к кривой
y = f (
x
) в любой точке ( x0
, f
( x0
) ), x0
Функция
f (
x
) называется вогнутой
на интервале ( a,
b
), если её график на этом интервале
лежит выше
касательной, проведенной к кривой
y = f (
x
) в любой точке ( x0
, f
( x0
) ), x0
Достаточное условие вогнутости ( выпуклости ) функции. Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда: если
f '' (
x
) > 0 для любого x
если
f '' (
x
) < 0 для любого x
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0 |
65.Теоремы Ферма,Ролля,Коши,Лагранжа Т.Ферма. Пусть
y=f(x)
определена на интервале (a,b)
и в некоторой точке
Тогда
если в т. Т.Ролля: Пусть y=f(x) непрерывна на [a,b],дифференцируема в каждой точке интервала (a,b) и выполняется соотношение f(a)=f(b) Тогда существует хотя бы одна т.сиз интервала (a,b),что f’(x) в с=0.
Т.Коши f(x)
и g(x)
непрерывна на [a,b]
дифференцируема на (a,b)
и
Т.Лагранжа(следствие из Т.Коши) Пусть
f(x)
и g(x)
непрерывна на [a,b]
дифференцируема на (a,b),тогда
внутри (a,b)
найдется такая т.с f(b)-f(a)=f’(c)(b-a) т.е.
Вопросы к экзамену по курсу "Математика" (I курс, I семестр) 1 Определение матрицы. Виды матриц. Линейные операции над матрицами 2 Произведения матриц. Свойства. 3 Теорема о разложении определителя по элементам ряда (на примере определителя 4 его порядка). 4 Свойства определителей. 5 Определение обратной матрицы и критерий существования обратной матрицы 6. Теорема о существовании единственной обратной матрицы 7. Определение системы линейных уравнений, запись в матричном виде Решение систем 8 Решение невырожденных систем линейных уравнений матричный метод и метод Крамера. 9 Определение ранга матрицы Методы нахождения ранга 10 Теорема Кренекера-Капелли. Правило решения произвольных линейных систем 11. Системы однородных линейных уравнений. 12 Межотраслевой баланс Технологическая матрица 13 Уравнение Леонтьева Критерий продуктивности матрицы. 14 Понятие вектора. Линейные операции над векторами. 15 Понятие базиса. Теорема о разложении вектора по базисным векторам в R3. 16 Скалярное произведение векторов: определение, свойства и приложения . 17. Векторное произведение векторов: определение, свойства и приложения . 18 Смешанное произведение векторов определение, свойства, приложения . 19. Различные формы уравнения прямой на плоскости. 20 Взаимное расположение прямых на плоскости 21 Расстояние от точки до прямой на плоскости ( вывод ). 22 Окружность - определение, каноническое уравнение, запись в полярных координатах 23. Эллипс-определение, вывод канонического уравнения 24. Основные характеристики эллипса. Теорема ( второе определение эллипса ) 25. Гипербола - определение, вывод канонического уравнения 26. Основные характеристики гиперболы. 27. Парабола -определение, вывод канонического уравнения. 28 Различные виды уравнений плоскости в пространстве. 29 Расстояние от точки до плоскости. Взаимное расположение плоскостей 30. Виды уравнений прямой в пространстве. 31 Взаимное расположение прямой и плоскости 32 Расстояние от точки до прямой в пространстве 33 Понятие скрещивающихся прямых Расстояние между скрещивающимися прямыми 34. Понятие функции, способы задания, основные элементарные функции. 35. Основные характеристики функций
|
66.Правило Лопиталя Данное
правило применяется при вычислении
пределов с неопределенностями
Т.1.(правило
Лопиталя Пусть
f(x)
и g(x)
непрерывны на [a,b],дифференцируемы
на (a,b)
и существует О( Предположим,что
Доказательство Определим
f(x)
и g(x)
в т.
Т.2(Правило
Лопиталя Пусть
f(x)
и g(x)
непрерывны и дифференцируемы в О( Тогда
если существует
Замечания 1.Правило Лопиталя можно применять неоднократно. 2.В
случае неопределенности
36 Понятие обратной и сложной функций. 37. Определение числовой последовательности и ее предела. 38 Теорема о пределе ограниченной последовательности. Определение верхней и нижней грани последовательности. 39 Теорема Вейерштрасса. 40 Вывод числа е 41 Определение предела функции в точке, геометрический смысл предела. 42. Определение односторонних пределов функции в точке. Предел на бесконечности. 43. Определение бесконечно больших и бесконечно малых функций Теорема об алгебраической сумме б.м.ф 44. Основные теоремы о б.м.ф. ( одна с доказательством ). 45. Теорема ( о единственности предела функции в точке ). 46 Теорема ( основные операции над пределами ). 47 Признаки существования предела функции в точке. 48. Замечательные пределы 49. Сравнение б.м.ф. Теорема об эквивалентных б.м.ф. 50. Три определения непрерывности функции в точке. 51 Основные теоремы о непрерывных функциях 52 Классификация точек разрыва. 53 Свойства функций, непрерывных на отрезке. 54 Определение комплексного числа, основные обозначения, алгебраическая форма. 55 Тригонометрическая форма комплексного числа, изображение на плоскости 56. Формула Муавра и формула корня п - ой степени для комплексного числа. 57. Комплексное число в показательной форме Формула Эйлера Действия над комплексными числами в показательной форме. 58. Определение производной функции в точке. Геометрический и механический смысл производной 59. Экономический смысл производной. Эластичность функции и ее свойства. 60. Основные правила дифференцирования 61 Таблица основных производных 62. Логарифмическая производная. Дифференцирование функций, заданных неявно и параметрически. 63. Дифференциал функции; его геометрический смысл. Применение дифференциала к приближенным вычислениям 64 Производные и дифференциалы высших порядков 65. Теоремы Ферма, Роля, Коши, Лагргнжа. 66. Правило Лопиталя 67 Условия монотонности функции Экстремум функции: необходимое условие, достаточные условия. 68 Наибольшее и наименьшее значение функции на отрезке. 69 Выпуклость вогнутость графика функции. Точки перегиба. 70 Асимптоты графика функции. Общая схема исследования функции |
||
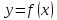 в точке
в точке
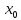 называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента стремится к
нулю.По определению
называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента стремится к
нулю.По определению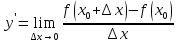 или
или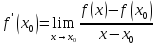
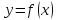 ,
имеющая производную в каждой точке
интервала называется дифференцируемой
в этом интервале, операция нахождения
производной функции называется
дифференцированием.
,
имеющая производную в каждой точке
интервала называется дифференцируемой
в этом интервале, операция нахождения
производной функции называется
дифференцированием.
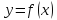 в точке
в точке
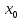 обозначается
обозначается
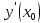 .
.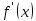 в точке х равно угловому коэффициенту
касательной к графику функции
в точке х равно угловому коэффициенту
касательной к графику функции
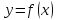 в точке, абсцисса которой равна х.
в точке, абсцисса которой равна х.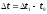 объем произведенной продукции
объем произведенной продукции

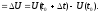
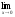 ,
то производная труда в момент времени
,
то производная труда в момент времени
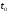 называется
пределом
называется
пределом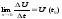
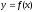 наз. величину
наз. величину
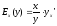 ,
которая выражает приближенный %- ный
прирост значения ф-ии при приросте
аргумента на 1%.
,
которая выражает приближенный %- ный
прирост значения ф-ии при приросте
аргумента на 1%.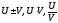
 также
дифф. в этой точке.
также
дифф. в этой точке.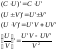
 y;
y;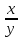 ;
;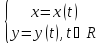 ;
;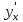 =
=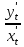 ;
;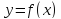 задана
явно.Производная от данной функции
задана
явно.Производная от данной функции
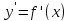 называется
производной первого порядка и также
является функцией от x.
называется
производной первого порядка и также
является функцией от x.
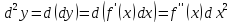
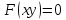 –
задана
неявно.
–
задана
неявно.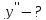
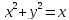 ,
х-дифференцируем.
,
х-дифференцируем.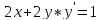
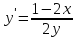 – дифференцируем
по Х.
– дифференцируем
по Х.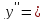
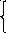 3.Параметрически.
3.Параметрически.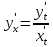
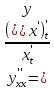
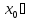 (a,b)
достигает локального экстремума.
(a,b)
достигает локального экстремума.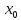 существует конечная производная,то
существует конечная производная,то
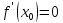
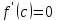
 для
всех
для
всех
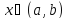 тогда
на (a,b)
найдется такая точка
с
тогда
на (a,b)
найдется такая точка
с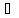 (a,b),
что
(a,b),
что
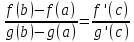
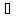 (a,b)
что
(a,b)
что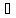 с
с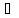 (a,b),
что хорда АВ параллельна касательной.
(a,b),
что хорда АВ параллельна касательной.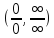
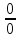 )
)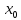 ),
за исключением быть может самой этой
точки.
),
за исключением быть может самой этой
точки.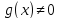 ,
,
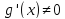 в
О(
в
О(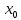 )
тогда если
)
тогда если
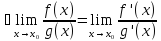
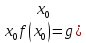 )=0
,тогда эти функции будут непрерывны
в т.
)=0
,тогда эти функции будут непрерывны
в т.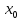 и по Т.Коши на [
и по Т.Коши на [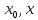 ]
будет выполняется неравенство.
]
будет выполняется неравенство.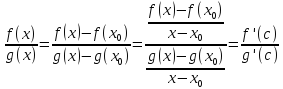
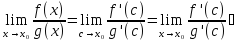
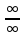 )
)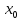 )
и
)
и
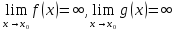
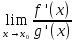 ,
то существует
,
то существует
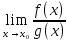 и
и
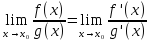
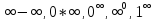 сначала сводятся к одной из
неопределенностей
сначала сводятся к одной из
неопределенностей
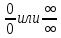 и применяется правило Лопиталя.
и применяется правило Лопиталя.