Файл: Задачи по теме Площади фигур.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.10.2024

Просмотров: 14

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Зачет по геометрии 9 класс

Тема «Площади фигур»

  1. Докажите, что площадь параллелограмма ABCD равна площади треугольника AMD, если точка С является серединой отрезка MD.

  2. Докажите, что медиана треугольника разбивает его на два равновеликих.

  3. Докажите, что диагонали параллелограмма разбивают его на 4 равновеликих треугольника.

  4. Докажите, что медианы треугольника делят его площадь на 6 равных частей.

  5. Докажите, что если диагональ какого-нибудь четырехугольника делит другую диагональ пополам, то она делит пополам и площадь четырехугольника.

  6. Точка О лежит на прямой, содержащей диагональ АС параллелограмма ABCD. Докажите, что площади треугольников АОВ и AОD равны.

  7. Внутри параллелограмма ABCD взята произвольная точка К. Докажите, что .

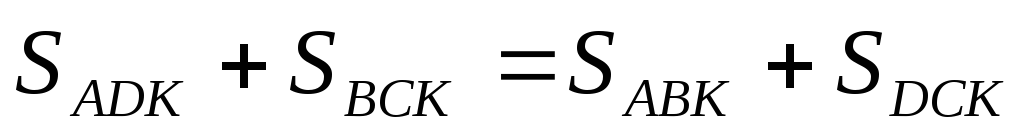  8. Найдите площадь прямоугольника, если его диагонали равны 12 и угол между диагоналями равен .

  9. В ромбе, со стороной равной 5 см, угол между стороной и диагональю 300. Найдите площадь ромба.

  10. В параллелограмме одна из сторон 10 см, а один из углов 300. Найдите площадь параллелограмма, если его периметр 56 см.

  11. Найдите углы параллелограмма, если его площадь равна 40 см2, а стороны 10 см и 8 см

  12. Стороны параллелограмма равны 12 см и 9 см, а угол между его высотами равен 300.Найдите площадь параллелограмма.

  13. Высоты, проведенные из вершин тупого угла параллелограмма, составляют угол в 450. Одна из высот дели сторону на которую она опущена, на отрезки 2 см и 8 см, считая от вершины острого угла. Найдите площадь параллелограмма.

  14. Докажите, что из всех треугольников, у которых одна сторона равна а, а другая – b, наибольшую площадь имеет тот, у которого эти стороны перпендикулярны.

  15. Высота прямоугольного треугольника, проведённая к гипотенузе, делит гипотенузу на отрезки длины 2 и 18. Найдите площадь этого треугольника.

  16. В треугольнике точка пересечения биссектрис удалена от прямой, содержащей одну из сторон, на 1,5 см. Найдите площадь треугольника, если его периметр равен 16 см.

  17. Основания трапеции относятся как 3:7. В каком отношении разделят площадь трапеции: а) ее диагональ; б) ее средняя линия; в) прямая, проходящая через вершину меньшего основания трапеции параллельно ее боковой стороне?

  18. Точка Е – середина стороны АВ треугольника АВС, а точки М и Н делят сторону ВС на три равные части, ВМ=МН=НС. Найдите площадь треугольника ЕМН, если площадь треугольника АВС равна s.

  19. Через концы средней линии треугольника проведены параллельные прямые, пересекающие его третью сторону. Докажите, что площадь образовавшегося параллелограмма вдвое меньше площади исходного треугольника.

  20. Докажите, что площадь произвольного выпуклого четырехугольника в 2 раза больше площади четырехугольника с вершинами в серединах сторон исходного.

  21. На сторонах АВ и АС треугольника АВС выбраны точки М и К соответственно. Найдите площадь четырехугольника МКСВ, если АМ=6 см, МВ=4 см, АК=4 см, АС=12 см, а площадь треугольника АМК равна 10 см2.

  22. Отрезок, соединяющий середины двух противоположных сторон выпуклого четырехугольника, разделил его на два равновеликих четырехугольника. Докажите, что эти стороны параллельны.

1

Смотрите также файлы