Добавлен: 21.10.2018
Просмотров: 344
Скачиваний: 5
Задачи
-
Используя диаграммы Венна, доказать тождество множеств:
A + ( B*C) = (A+B)*(A+C), где “+” – объединение, “*” – пересечение.
-
Дать определение свойствам бинарных отношений: рефлексивности, симметричности, транзитивности.
-
Дать определение отношению эквивалентности. Привести три примера отношения эквивалентности.
-
Построить векторную форму БФ, двойственной к F(X,Y) = X
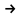 Y;
Y;
-
Задана БФ F(X,Y) = X v Y; Построить векторную форму такой БФ G(X,Y,Z), которая была бы равна заданной БФ F(X,Y).
-
Пусть X и Y множества БФ, а [X] и [Y] – замыкания этих множеств. Каким знаком (
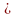 ,
,
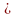 ,
,
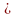 ,
,
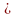 ,
,
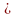 ,
,
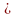 ),
Вы соединили бы выражения [X]
),
Вы соединили бы выражения [X]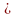 [Y]
и [X
[Y]
и [X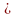 Y],
чтобы получить заведомо истинное
утверждение (укажите порядковый номер
знака в приведённом списке).
Y],
чтобы получить заведомо истинное
утверждение (укажите порядковый номер
знака в приведённом списке).
-
Сколько всего БФ из списка: X
 Y, X|Y, 0, ¬ X входит во множество [ v , ¬ ] (
[S] означает замыкание S)? Укажите число
от 0 до 4.
Y, X|Y, 0, ¬ X входит во множество [ v , ¬ ] (
[S] означает замыкание S)? Укажите число
от 0 до 4.
-
Для функции X
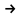 Y
постройте СДНФ.
Y
постройте СДНФ.
-
Для функции X v Y постройте СКНФ.
-
Для функции X
 Y постройте полином
Жегалкина.
Y постройте полином
Жегалкина.
-
Исследуйте функцию X
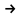 Y
на принадлежность её эталонным классам
T0, T1, S,
M, L. В
качестве ответа приведите строку из
знаков ‘+’ и ‘-‘ в соответствующей
таблице .
Y
на принадлежность её эталонным классам
T0, T1, S,
M, L. В
качестве ответа приведите строку из
знаков ‘+’ и ‘-‘ в соответствующей
таблице .
-
По теореме Поста о полноте докажите полноту класса БФ {
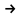 ,
0}
,
0}
-
Для функции f, заданной вектором
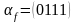 ,
определить, является ли она:
,
определить, является ли она:
-
линейной
-
монотонной
-
самодвойственной
-
функцией из класса
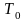
-
функцией из класса
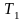
-
Полна ли система функций {f, g, h} (принадлежность функций классам
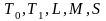 отображена
в таблице).
отображена
в таблице).

-
Полна ли система функций {f, g, h} (принадлежность функций классам
 отображена
в таблице).
отображена
в таблице).

-
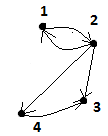 Для
заданного орграфа построить матрицу
смежности.
Для
заданного орграфа построить матрицу
смежности.
-
Планарен ли следующий граф (ответ обосновать):
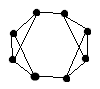
-
Является ли планарным следующий граф (ответ обосновать):
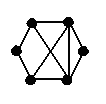
-
Построить (нарисовать) орграф по следующей матрице смежности:
__|_1 2 3 4 5
1 | 1 0 0 0 1
2 | 0 1 1 0 1
3 | 0 0 0 0 0
4 | 1 1 1 0 0
5 | 0 0 1 0 1
-
Построить бинарный код следующего корневого дерева:
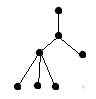
-
Воссоздать корневое дерево по следующему его бинарному
коду: 01001 001 1101
-
Построить прямой, обратный и концевой обход бинарного дерева:
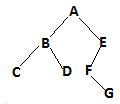
-
Воссоздать бинарное дерево по заданным его обходам:
ABCDEF (прямому) и BCAEDF (обратному).
-
Перевести в ПОЛИЗ следующее выражение: “(a+b*c) / ln(2a)”
-
Вычислить значение следующего заданного в ПОЛИЗ выражения:
“ 4, 3, 7, +, 5, /, sqr, - “
-
Построить пример допустимого потока в следующей сети:
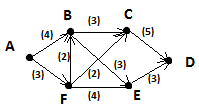
-
Задана схема побуквенного двоичного кодирования: (10
 a, 01
a, 01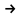 b,
110
b,
110
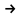 c,
111
c,
111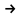 d).
d).
-
Используя её, декодировать сообщение: 11010100110110
-
Исследовать её на однозначность.
-
Используя алгоритм сжатия Лемпела-Зива, закодировать текст:
abaababaaaa
-
Восcтановить текст, если результатом его сжатия по методу Лемпела-Зива явилась следующая таблица:
G: | < 0, a >
| < 0, b >
| < 1, a >
| < 2, a >
| < 3, b >