Файл: 1 семинар.docx

Скачать файл (0,06Мб)

Заказать решение

ВУЗ: Не указан

Категория: Задание

Дисциплина: Не указана

Добавлен: 21.10.2018

Просмотров: 526

Скачиваний: 17

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Задача 1.

Рассчитать оптимальное время проведения химической реакции в аппарате идеального смешения, приняв в качестве критерия оптимальности выход целевого продукта P.

Схема реакции:

Порядок обеих стадий реакции – первый. Константы скоростей равны:

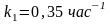
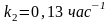
Решение

Материальный баланс по компонентам A и P:

При делении уравнений на расход реагента v получаем:

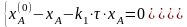
где - среднее время пребывания реагентов в реакторе

Выход продукта P выражается:

Необходимое условие существования экстремума:

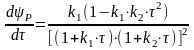
Поскольку 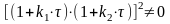и

Условие экстремума будет иметь вид:

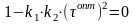
Откуда:

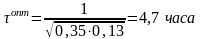
Программа:

Model1_tau (построение графиков xa от T и xp от T. Графическое решение задачи. Поиск экстремума. Программа расчета оптимального времени пребывания (tau - час) в изотермическом реакторе идеального смешения со стехиометрической схемой реакции A - P –S)

Файл DATA.m

Программный код файла DATA.m - задание исходной информации для расчетов

function DATA

global xa0 k1 k2 tau_a tau_b;

Концентрация реагента А в долях в реакции A-P-S (мольные доли)

xa0=1;

Константы скоростей реакций (час^(-1))

k1=0.35; k2=0.13;

Левая граница поиска оптимального времени пребывания в реакторе (час)

tau_a=1;

Правая граница поиска оптимального времени пребывания в реакторе (час)

tau_b=10;

end

Файл model1_stat_tau .m

Программный код файла model1_stat_tau .m - расчет выходных концентраций продуктов из реактора

Значения вектора х функции model1_stat_tau зависят от параметра « tau»

function x= model1_stat_tau(tau)

global xa0 k1 k2;

Обнуляем матрицу a и вектор b

a=zeros(2,2);b=zeros(2,1);

Для решения системы уравнений используем метод обратной матрицы.

Преобразуем систему уравнений:

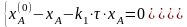
чтобы получить коэффициенты матрицы:

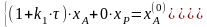
Задание коэффициентов матрицы А (коэффициенты перед 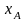и ) и

вектора В (коэффициенты правой части системы уравнений,

после знака «равно») .

a(1,1)=1+k1*tau;a(1,2)=0;b(1)=xa0;

a(2,1)=tau*k1;a(2,2)=(-1-tau*k2); b(2)=0;

Определение выходных параметров модели. А=х*В. х=А/В. х=А^-1*В

x=inv(a)*b;

Оператор inv(а) - поиск обратной матрицы А

end

Файл GLAV_maximum_phi_p.m

Программный код файла GLAV_maximum_phi_p.m - главная управляющая программа

clc;

clear all;

close all;

global t xa xp tau_a tau_b;

i=0;

DATA;

Задаем значение коэффициента tau (время пребывания в реакторе, мин) в интервале от tau_a до tau_b с шагом 0.1

for tau=tau_a:0.1:tau_b

i=i+1;

Вызываем функцию x= model1_stat_tau(tau)

x= model1_stat_tau(tau);

Массив значений коэффициента tau(мин) в интервале от tau_a до tau_b с шагом 0.1

t(i)=tau;

Массив значений коэффициента ха (мол.дол) - концентрации продукта А на выходе из реактора в заданном интервале температур от tau_a до tau_b

xa(i)=x(1);

Массив значений коэффициента ха (мол.дол) - концентрации продукта P на выходе из реактора в заданном интервале температур от tau_a до tau_b

xp(i)=x(2);

end

REPORT;

Файл REPORT.m

Программный код файла REPORT.m - отчет о работе программы

global xa0 k1 k2 t xa xp tau_a tau_b;

Выводим на экран необходимый текст.

disp('ПРОГРАММА МОДЕЛИРОВАНИЯ ИЗОТЕРМИЧЕСКОГО РЕАКТОРА ИДЕАЛЬНОГО ПЕРЕМЕШИВАНИЯ ');

disp(' РЕАКЦИЯ : A - P - S' );

disp('-------------------------------------------------');

disp('Программа включает следующие файлы: GLAV_model1_grafik.m+DATA.m+model1_stat_tau+REPORT.m');

disp('_____________________________________________________________ ');

disp('ИСХОДНЫЕ ДАННЫЕ ');

disp('-------------------------------------------------');

Оператор num2str(xa0,'%10.2f') переводит числовые значения в строковые.

Для этого необходимо записать оператор num2str, далее в скобках указываем переменную, которую необходимо перевести в строковый формат «xa0», затем ставим запятую «,» либо пробел и в одинарных кавычках через точку указываем число символов (%10) в строковой переменной и количество знаков после запятой(2f).

disp(['1.Концентрация реагента A на входе в реактор ( xa0 ) = ' num2str(xa0,'%10.2f') ' мольные доли']);

disp('--------------------------------------------------------');

disp(['2.Константа скорости первой элементарной реакции ( k1) = ' num2str(k1,'%10.2f') ' час^(-1)']);

disp(['3.Константа скорости второй элементарной реакции ( k2) = ' num2str(k2,'%10.2f') ' час^(-1)']);

disp('--------------------------------------------------------');

disp(['4.Левая граница интервала поиска оптимального времени пребывания в реакторе ( tau_a) = ' num2str(tau_a,'%10.2f') ' час']);

disp('--------------------------------------------------------');

disp(['5. Правая граница интервала поиска оптимального времени пребывания в реакторе( tau_b) = ' num2str(tau_b,'%10.2f') ' час']);

disp('____________________________________________________________ ');

disp('---------------------------------------------');

disp ('РЕЗУЛЬТАТЫ РАСЧЕТОВ');

disp('------------------------------------------------');

disp('--------------------------------------------');

disp ('1.Концентрации продуктов на выходе из реактора');

disp('--------------------------------------------------');

disp('_____________________________')

disp(' tau(час) xa(мол.д.) xp(мол.д.) ');

disp('_____________________________')

i=0;

Выводим таблицу данных. Переменные t, xa, xp;

for i=1:length(t)

tt=t(i);xaa=xa(i);xpp=xp(i);

disp(sprintf('%10.3f\t %10.5f\t %10.5f',tt,xaa,xpp));

end

Построение графиков

hfig(1)=figure;

hfig(2)=figure;

Рисунок 1. График зависимости выхода продукта A от времени пребывания в реакторе.

figure(hfig(1));

Построение графика

plot(t,xa);

Название графика

title('График зависимости выхода продукта A от времени пребывания в реакторе');

Подписи осей графика.

xlabel('tau - час');ylabel('Выходные концентрации : xa - мольные доли');

Наложение сетки на график

grid on;

Рисунок 2. График зависимости выхода продукта P от времени пребывания в реакторе

figure(hfig(2));

Построение графика

plot(t,xp);

Название графика

title('График зависимости выхода продукта P от времени пребывания в реакторе');

Подписи осей графика.

xlabel('tau - час');ylabel('Выходные концентрации : xp - мольные доли');

Наложение сетки на график

grid on;

end

ОТЧЕТ

ПРОГРАММА МОДЕЛИРОВАНИЯ ИЗОТЕРМИЧЕСКОГО РЕАКТОРА ИДЕАЛЬНОГО ПЕРЕМЕШИВАНИЯ

РЕАКЦИЯ : A - P - S

-------------------------------------------------

Программа включает следующие файлы: GLAV_model1_grafik.m+DATA.m+model1_stat_tau+REPORT.m

_____________________________________________________________

ИСХОДНЫЕ ДАННЫЕ

-------------------------------------------------

1.Концентрация реагента A на входе в реактор ( xa0 ) = 1.00 мольные доли

--------------------------------------------------------

2.Константа скорости первой элементарной реакции ( k1) = 0.35 час^(-1)

3.Константа скорости второй элементарной реакции ( k2) = 0.13 час^(-1)

--------------------------------------------------------

4.Левая граница интервала поиска оптимального времени пребывания в реакторе ( tau_a) = 1.00 час

--------------------------------------------------------

5. Правая граница интервала поиска оптимального времени пребывания в реакторе( tau_b) = 10.00 час

____________________________________________________________

---------------------------------------------

РЕЗУЛЬТАТЫ РАСЧЕТОВ

------------------------------------------------

--------------------------------------------

1.Концентрации продуктов на выходе из реактора

--------------------------------------------------

_____________________________

tau(час) xa(мол.д.) xp(мол.д.)

_____________________________

1.000 0.74074 0.22943

1.100 0.72202 0.24320

1.200 0.70423 0.25586

1.300 0.68729 0.26751

1.400 0.67114 0.27822

1.500 0.65574 0.28809

1.600 0.64103 0.29716

1.700 0.62696 0.30552

1.800 0.61350 0.31321

1.900 0.60060 0.32029

2.000 0.58824 0.32680

2.100 0.57637 0.33278

2.200 0.56497 0.33828

2.300 0.55402 0.34333

2.400 0.54348 0.34796

2.500 0.53333 0.35220

2.600 0.52356 0.35608

2.700 0.51414 0.35963

2.800 0.50505 0.36287

2.900 0.49628 0.36581

3.000 0.48780 0.36849

3.100 0.47962 0.37091

3.200 0.47170 0.37309

3.300 0.46404 0.37506

3.400 0.45662 0.37682

3.500 0.44944 0.37839

3.600 0.44248 0.37978

3.700 0.43573 0.38101

3.800 0.42918 0.38207

3.900 0.42283 0.38299

4.000 0.41667 0.38377

4.100 0.41068 0.38442

4.200 0.40486 0.38496

4.300 0.39920 0.38537

4.400 0.39370 0.38569

4.500 0.38835 0.38590

4.600 0.38314 0.38602

4.700 0.37807 0.38605

4.800 0.37313 0.38600

4.900 0.36832 0.38587

5.000 0.36364 0.38567

5.100 0.35907 0.38541

5.200 0.35461 0.38508

5.300 0.35026 0.38469

5.400 0.34602 0.38424

5.500 0.34188 0.38374

5.600 0.33784 0.38320

5.700 0.33389 0.38260

5.800 0.33003 0.38197

5.900 0.32626 0.38129

6.000 0.32258 0.38057

6.100 0.31898 0.37982

6.200 0.31546 0.37904

6.300 0.31201 0.37822

6.400 0.30864 0.37738

6.500 0.30534 0.37651

6.600 0.30211 0.37561

6.700 0.29895 0.37469

6.800 0.29586 0.37375

6.900 0.29283 0.37279

7.000 0.28986 0.37180

7.100 0.28694 0.37080

7.200 0.28409 0.36979

7.300 0.28129 0.36876

7.400 0.27855 0.36771

7.500 0.27586 0.36665

7.600 0.27322 0.36558

7.700 0.27064 0.36450

7.800 0.26810 0.36341

7.900 0.26560 0.36231

8.000 0.26316 0.36120

8.100 0.26076 0.36008

8.200 0.25840 0.35896

8.300 0.25608 0.35782

8.400 0.25381 0.35669

8.500 0.25157 0.35555

8.600 0.24938 0.35440

8.700 0.24722 0.35325

8.800 0.24510 0.35210

8.900 0.24301 0.35094

9.000 0.24096 0.34979

9.100 0.23895 0.34863

9.200 0.23697 0.34747

9.300 0.23502 0.34630

9.400 0.23310 0.34514

9.500 0.23121 0.34398

9.600 0.22936 0.34281

9.700 0.22753 0.34165

9.800 0.22573 0.34049

9.900 0.22396 0.33932

10.000 0.22222 0.33816

Optim1_tau (Оптимальные значения режимных параметров реактора: времени пребывания, концентрации продукта А на выходе из реактора, концентрации продукта Р на выходе из реактора. Программа расчета оптимального времени пребывания (tau - час) в изотермическом реакторе идеального смешения со стехиометрической схемой реакции A - P –S)

Файл DATA.m

Программный код файла DATA.m - задание исходной информации для расчетов

function DATA

global xa0 k1 k2 tau_a tau_b;

Концентрация реагента А в долях в реакции A-P-S (мольные доли)

xa0=1;

Константы скоростей реакций (час^(-1))

k1=0.35; k2=0.13;

Левая граница поиска оптимального времени пребывания в реакторе (час)

tau_a=1;

Правая граница поиска оптимального времени пребывания в реакторе (час)

tau_b=5;

end

Файл model1_stat_tau.m

Программный код файла model1_stat_tau .m - расчет выходных концентраций продуктов из реактора

Значения параметра phi_p функции model1_stat_tau зависят от параметра «tau»

function phi_p= model1_stat_tau(tau)

global xa0 k1 k2 xa xp;

Обнуляем матрицу a и вектор b

a=zeros(2,2);b=zeros(2,1);

Для решения системы уравнений используем метод обратной матрицы.

Преобразуем систему уравнений:

чтобы получить коэффициенты матрицы:

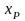Задание коэффициентов матрицы А (коэффициенты перед и ) и

вектора В (коэффициенты правой части системы уравнений,

после знака «равно») .

a(1,1)=1+k1*tau;a(1,2)=0;b(1)=xa0;

a(2,1)=tau*k1;a(2,2)=(-1-tau*k2); b(2)=0;

Определение выходных параметров модели. А=х*В. х=А/В. х=А^-1*В

Оператор inv(а) - поиск обратной матрицы А

x=inv(a)*b; xa=x(1);xp=x(2);

Вычисление критерия оптимальности phi_p (целевой функции );

В дальнейшем будет использоваться оператор «fminbnd», который находит минимум функции. Для того чтобы найти максимум функции с помощью оператора «fminbnd», мы ставим знак «-» перед x(2)/xa0

phi_p=-x(2)/xa0;

end

Файл GLAV_maximum_phi_p.m

Программный код файла GLAV_maximum_phi_p.m - главная управляющая программа

clc;

clear all;

close all;

global tau_opt phi_p_max tau_a tau_b;

DATA;

disp('Информация об итерационном процессе расчета');

Информация об итерационном процессе расчета

iteration=optimset('Display','iter');

Реализация алгоритма поиска максимума функции одной переменной

[tau_opt,phi_p]=fminbnd('model1_stat_tau',tau_a,tau_b,iteration);

Знак «-» перед phi_p необходим для корректного вывода данных экстремума функции. Оператор «fminbnd» находит минимум функции со знаком «-». Нам нужен максимум функции со знаком «+».

phi_p_max=-phi_p;

REPORT;

Файл REPORT

function REPORT

Программный код файла REPORT.m - отчет о работе программы

global xa0 k1 k2 tau_opt phi_p_max xa xp tau_a tau_b;

Выводим на экран необходимый текст.

disp('ПРОГРАММА ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО АРЕМЕНИ ПРЕБЫВАНИЯ');

disp('В ИЗОТЕРМИЧЕСКОМ РЕАКТОРE ИДЕАЛЬНОГО ПЕРЕМЕШИВАНИЯ ');

disp(' РЕАКЦИЯ : A - P - S' );

disp('-------------------------------------------------');

disp('Программа : GLAV_maximum_phi_p.m+DATA.m+model1_stat_tau.m+REPORT.m');