Файл: ДКР Информационные технологии 2Б.docx

Р = 20х₁ + 24х₂ + 28х₃ → mах

Сформулируем задачу: требуется найти х₁, х₂, х₃, дающие максимум це­левой функции Р при заданных ограничениях.

В пакете Excel данная задача решается с помощью команды Поиск решения. Если на вкладке Данные отсутствует команда Поиск решения, то для ее установки необходимо выполнить команду Office - Параметры, Надстройки - Выделить строку Пакет анализа и щелкнуть по кнопке Пе­рейти - поставить флажок Поиск Решения и нажать ОК. После этого на вкладке Данные в группе Анализ появится команда Поиск Решения.

Для решения оптимизационной задачи необходимо выполнить следую­щие действия:

а) подготовить электронную таблицу с исходными данными (рисунок 1):

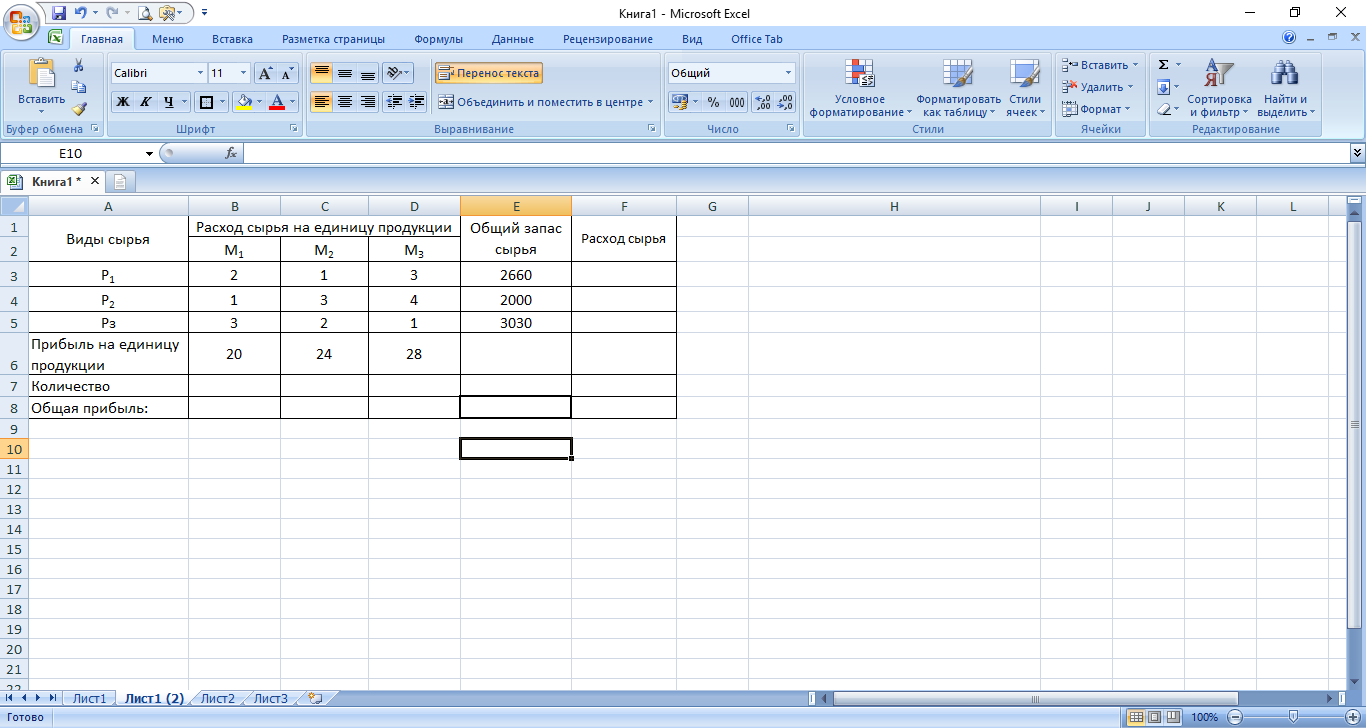
Рисунок 1 - Электронная таблица для решения задачи с исходными данными

• Отведем ячейки В7:D7 под значения переменных, введя туда про­извольные начальные приближения, например, х₁ = 1, х₂ = 1, x₃ = 1.

• В ячейки F3:F5 введём формулы левых частей ограничений:

= 2x₁ + x₂ + 3x₃

= x₁ + 3x₂ + 4x₃

= 3x₁ + 2x₂ + x₃

• В ячейки В8:D8 введём общую прибыль каждой продукции.

• В ячейку Е8 введем функцию цели (общую прибыль продукции):

= 20x_x + 24x₂ + 28x₃

В режиме отображения формул эта таблица представлена на рисунке 2.

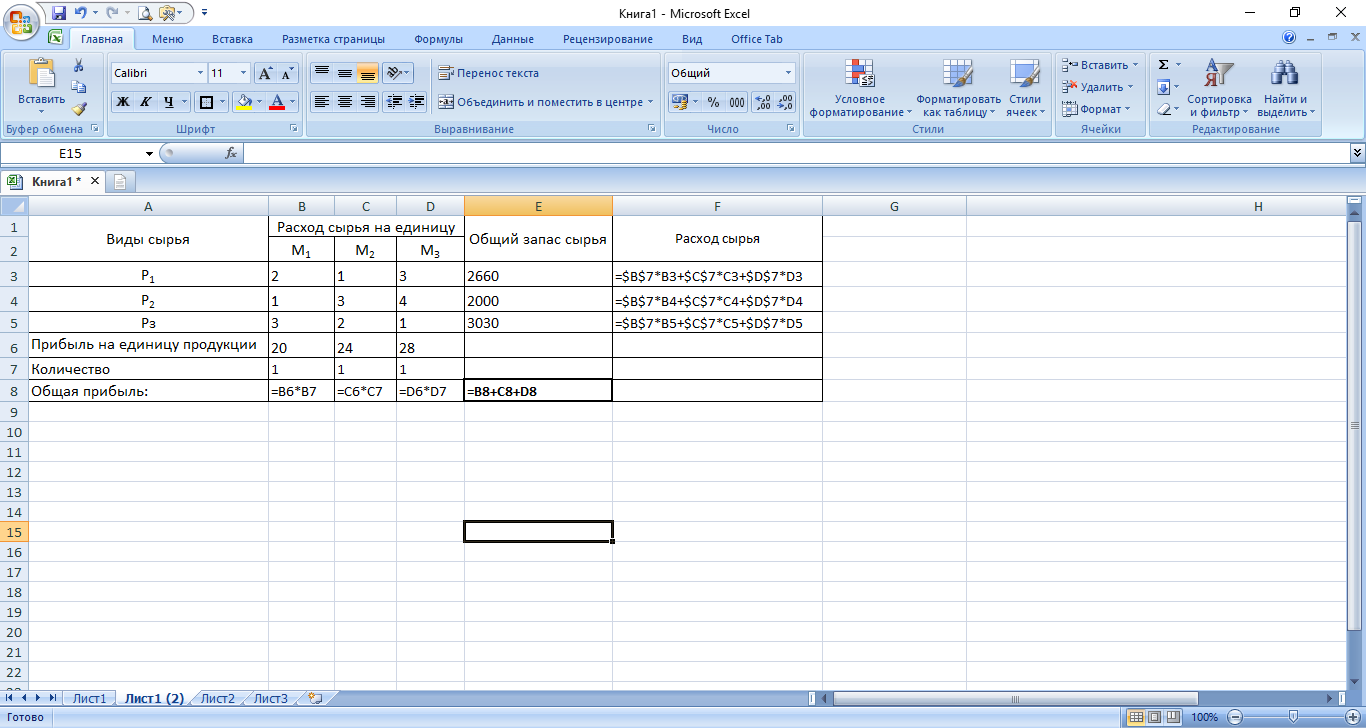
Рисунок 2 - Электронная таблица для решения задачи в режиме отображения формул

В режиме отображения значений эта таблица представлена на рисунке 3.

Рисунок 3 - Электронная таблица для решения задачи

б) После этого выберем команду Данные - Поиск решения и запол­ним открывшееся диалоговое окно Поиск решения (рисунок 4).

В поле Установить целевую ячейку дается ссылка на ячейку с функ­цией, для которой будет находиться максимум, минимум или заданное зна­чение. В нашей задаче в это поле вводим $Е$8.

Тип взаимосвязи между решением и целевой ячейкой задается путем установки переключателя в группе Равной. Для нахождения минимального или максимального значения функции этот переключатель ставится в поло­жение Maксимальному значению или Muнимальному значению соответ­ственно, для нахождения значения целевой функции, равного некоторому числу, переключатель ставится в положение 3начения. Тогда в соответст­вующее поле вводится требуемое число.

В поле Изменяя ячейки указываются ячейки, которые должны изме­няться в процессе поиска решения задачи, т.е. ячейки, отведенные под пере­менные задачи. В нашем случае вводим в это поле диапазон $В$7 : $D$7.

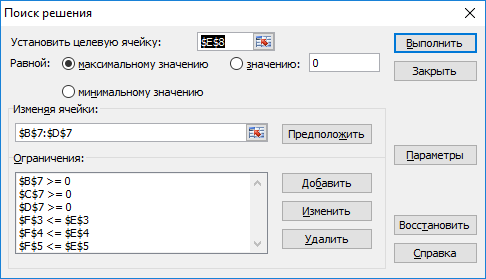
Рисунок 4- Диалоговое окно Поиск решения

Ограничения, налагаемые на переменные задачи, отображаются в поле Ограничения. Средство Поиск решения допускает ограничения в виде ра­венств, неравенств, а также позволяет ввести требование целочисленности переменных. Ограничения добавляются по одному. Для ввода ограничений следует нажать кнопку Добавить в диалоговом окне Поиск решения и в от­крывшемся диалоговом окне Добавление ограничения заполнить поля (ри­сунок 5).

---

Рисунок 5 - Диалоговое окно Добавление ограничения

В поле Ссылка на ячейки вводится первая часть ограничения - $F$3(щелчком по соответствующей ячейке), а в поле Ограничение - правая часть - $E$3. С помощью раскрывающегося списка вводится тип соотноше­ния между левой и правой частями ограничения (<,=,>,>=,<, цел). В нашем примере это знак <=

3атем следует нажать кнопку Добавить в диалоговом окне Добавление ограничения и ввести поочерёдно следующие ограничения, налагаемые на переменные. Нажатие кнопки ОК завершает ввод ограничений. Они отобра­зятся в окне диалога Поиск решения.

Кнопки Добавить, Изменить и Удалить позволяют, соответственно, ввести дополнительное ограничение, изменить вид выделенного в списке ог­раничения или удалить его.

в) Для определения параметров процедуры оптимизации (при необходи­мости) следует нажать кнопку Параметры в диалоговом окне Поиск реше­ния. В открывшемся диалоговом окне Параметры можно изменять условия и варианты поиска решения исследуемой задачи. Рассмотрим элементы этого окна (рисунок 6).

Рисунок 6 - Диалоговое окно Параметры поиска решения

Поле Максимальное время служит для ограничения времени, отпус­каемого на поиск решения. Время не должно превышать 32767 сек., что со­ставляет = 9,1 часа. По умолчанию задается 100 секунд.

Поле Предельное число итераций служит для управления временем решения зада­чи путем ограничения числа вычислений.

Поле Допустимое отклонение служит для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. В таких задачах в начале нахо­дится оптимальное нецелочисленное решение, а потом ищется ближайшая целочисленная точка, решение в которой отличалось бы от оптимального не более чем на указанное данным параметром количество процентов. При большом допуске может быть потеряно лучшее целочисленное решение, правда, отличающееся от найденного в пределах допуска. Для целочислен­ных задач имеет смысл уменьшить допуск.

Флажок Автоматическое масштабирование служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине (например, минимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах руб.).

Флажок Показывать результаты итераций задает приостановку по­иска решения для просмотра результатов итераций в специальном окне диа­лога. Целесообразно устанавливать, если требуется оценить число итераций, необходимое для решения той или иной задачи или проанализировать весь процесс движения к оптимальной точке.

Поле Относительная погрешность используется для задания точности (чис­ло из интервала (0; l), определяющее соответствие ячейки целевому значе­нию или приближение к указанным границам). Заметим, что иногда проще изменить ограничение, отодвинув границу, чем пытаться выполнить ограни­чение с высокой точностью.

---

г) После установки необходимых параметров следует нажать кнопку ОК и затем в окне Поиск решения нажать кнопку Выполнить.

Откроется окно Результаты поиска решения (рисунок 7), которое со­общает, что решение найдено (не найдено), (или будет выведено сообщение, позволяющее установить причину прекращения решения задачи, например в том случае, когда пустое множество допустимых решений или происходит зацикливание итерационной процедуры).

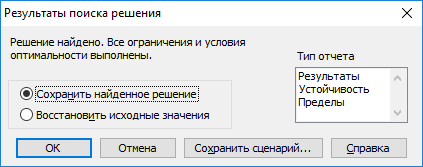
Рисунок 7 - Диалоговое окно Результаты поиска решения

Установив переключатель в положение Сохранить найденное реше­ние, можно сохранить найденное решение задачи в соответствующих ячей­ках электронной таблицы. В ячейках В7:D7 появятся оптимальные значения переменных, а в ячейке E8 - максимальное значение целевой функции.

Результаты решения представлены на рисунке 8.

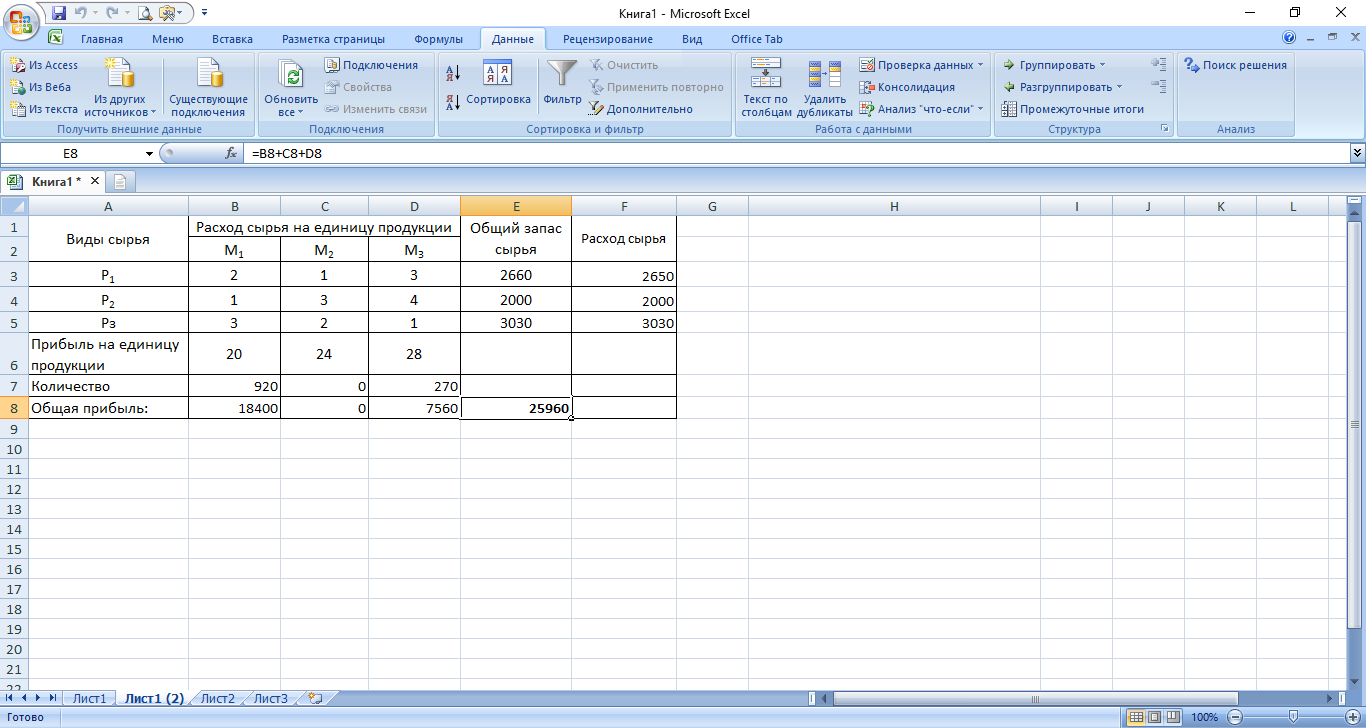
Рисунок 8- Результаты решения задачи

На основе полученных результатов можно сделать следующий вывод: Кондитерскому цеху надо выпустить продукции первого вида M₁ в количест­ве 920 усл. единиц, третьего вида M₃ - в количестве 270 усл. единиц, про­дукцию второго вида М₂ выпускать невыгодно. При таком плане выпуска продукции с учётом имеющихся ограничений будет получена максимальная прибыль в размере 25960 усл. единиц.

Для получения информации о ходе решения задачи в списке Тип отче­та можно выбрать отчет, который разместится на отдельном листе книги. Возможны следующие виды отчётов:

Результаты - используется для создания отчета, содержащего сведе­ния о времени решения задачи, числе итераций, параметрах поиска решения, сведений о целевой функции, ячейках с переменными и ограничениях.

Устойчивость - отчет содержит сведения о чувствительности решения к малым изменениям в формуле целевой функции или формулах ограниче­ний. Этот отчет имеет 2 раздела: один для изменяемых ячеек, а второй для ограничений. Правый столбец в каждой ячейке содержит информацию о чув­ствительности. Раздел для изменяемых ячеек содержит значение для норми­рованного коэффициента, которое показывает, как целевая ячейка реагирует на увеличение значения в соответствующей изменяемой ячейке на одну еди­ницу. Подобным образом множитель Лагранжа в разделе для ограничений показывает, как целевая ячейка реагирует на увеличение соответствующего значения ограничения на одну единицу.

Пределы - отчет содержит ячейку целевой функции, список исходных ячеек задачи, их значений, а также верхних и нижних границ этих значений. Нижняя и верхняя границы - это соответственно, минимальное и максималь­ное значения, которые могут принимать ячейки с переменными при соблю­дении ограничений.

Информационное обеспечение:

1. Михеева Е.В. Информационные технологии в профессиональной деятельности: учеб. пособие. – М.:ОИЦ «Академия», 2012, стр. 127-158.

2. Филимонова Е.В. Информационные технологии в профессиональной деятельности: учебник – Ростов н/Д: Феникс, 2012, стр. 131-161.

---

Задание 5

Условие транспортной задачи задано величинами a_j– запасов поставщиков, b_j–потребностей потребителей, с_ij – тарифов на перевозку грузов. Требуется составить план перевозок груза с минимальными транспортными издержками. Решить задачу в Excel.

Номера заданий

№1	bj aj	7	7	7	7	2	№2	bj aj		19		19		19		19		4
	4	16	30	17	10	16		20		15		11		22		19		1
	6	30	27	26	9	23		20		21		18		11		4		3
	10	13	4	22	3	1		20		26		29		23		26		24
	10	3	1	5	4	24		20		21		10		3		19		27
№3	bj aj	9	24	9	9	9	№4	bj aj		15		15		15		15		20
	15	10	17	9	20	30		21		30		24		11		12		25
	15	13	4	24	26	26		19		26		4		29		20		24
	19	22	24	30	27	29		15		27		14		14		10		18
	11	25	12	11	24	23		25		6		14		28		8		2
№5	bj aj	11	11	11	11	16	№6	bj aj		8		9		13		8		12
	15	17	20	29	26	25		9		5		15		3		6		10
	15	3	4	5	15	24		11		23		8		13		27		12
	15	19	2	22	4	13		14		30		1		5		24		25
	15	20	27	1	17	19		16		8		26		7		28		9
№7	bj aj	12	12	12	12	12	№8		bj aj		7		7		7		7		42
	13	20	23	24	26	29			22		9		17		29		28		8
	17	15	20	29	26	23			13		13		21		27		16		29
	17	4	10	27	30	7			17		20		30		24		7		26
	13	9	16	29	20	3			18		11		19		30		6		2
№9	bj aj	8	8	8	8	28	№10		bj aj		6		6		13		20		15
	18	21	22	2	13	7			16		30		2		5		6		15
	12	27	10	4	24	9			15		5		29		9		5		7
	17	3	16	25	5	4			14		16		24		14		6		26
	13	28	11	17	10	29			15		13		28		4		25		8

---

---