ВУЗ: Дальневосточный государственный университет путей сообщения
Категория: Методичка
Дисциплина: Информационные системы в экономике
Добавлен: 21.10.2018
Просмотров: 1411
Скачиваний: 5

16
Для написания математической модели закрытой транспортной задачи необ-
ходимо все условия (ограничения) и целевую функцию представить в виде мате-
матических соотношений. Все грузы должны быть отправлены. Все пункты
должны быть обеспечены грузами в плановом объеме. Должно выполняться
условие неотрицательности переменных. Перевозки необходимо осуществить с
минимальными транспортными издержками. Уравнение баланса является обяза-
тельным условием решения закрытой транспортной задачи, поэтому, когда в ис-
ходных условиях дана открытая задача, то ее необходимо привести к закрытой
форме: ввести фиктивного поставщика или фиктивного потребителя. Варианты,
связывающие фиктивные пункты с реальными, имеют нулевые оценки.
Целевая функция, которую следует минимизировать, записывается так:
Z = C
11
X
11
+ C
12
X
12
+ … + C
1m
X
1m
+ C
21
X
21
+ C
12
X
12
+ … +
+ C
2m
X
2m
+ … + C
n1
X
n1
+ C
n2
X
n2
+ … + C
nm
X
nm
.
Ограничения для сбалансированной задачи:
1. Сумма грузов, отправленных из любого пункта отправления, должна рав-
няться запасу грузов в этом пункте отправления:
х
11
+ х
12
+ … + х
1m
= а
1
,
……………………………..
х
n1
+ х
n2
+ … + х
nm
= а
n
.
2.
Сумма грузов, полученных в любом пункте назначения, должна равняться
объему грузов заказанных в этом пункте назначения:
х
11
+ х
21
+ … + х
n1
= b
1
,
………………………………..
х
1m
+ х
2m
+ … + х
nm
= b
m
.
В соответствии с транспортной таблицей левые части ограничений первой
группы – это суммы элементов матрицы X по строкам, которые равны соответ-
ствующим значениям правого столбца этой таблицы. Аналогично левые части
ограничений второй группы – суммы элементов матрицы X по столбцам, кото-
рые равны числам нижней строки таблицы.
Ограничения для задачи с дефицитом отличаются: сумма грузов, получен-
ных в любом пункте назначения, меньше объема грузов заказанных в этом пункте
назначения:
х
11
+ х
21
+ … + х
n1
≤ b
1
,
………………………………..
х
1m
+ х
2m
+ … + х
nm
≤ b
m
.
Подобным образом составляются ограничения для задачи с избытком.
Пример. Компания «Прибой» хранит свою готовую продукцию на трех скла-
дах (С1, С2 и С3), расположенных в разных частях города в количествах 1000, 3000
и 2500 шт. соответственно. Продукцию необходимо доставить четырем оптовым
покупателям П1, П2, ПЗ, П4, заявки которых составляют 1300, 800, 2700 и 1700
17
штук соответственно. Стоимость (в рублях) доставки одной единицы продукции
со складов компании на склады покупателей показаны в табл. 2.16.
Таблица 2.16
Транспортные расходы
Номер склада компании
Оптовые покупатели
П1
П2
ПЗ
П4
С1
50
150
60
75
С2
100
30
100
40
С3
70
180
210
120
Данная задача сбалансирована, т. е. запасы продукции и потребность в ней
равны. Построим математическую модель. Неизвестными здесь являются объ-
емы перевозок. Функцией цели являются суммарные транспортные расходы.
В соответствии с введенными переменными целевая функция запишется сле-
дующим образом:
Z = C
11
X
11
+ C
12
X
12
+ … + C
1m
X
1m
+ C
21
X
21
+ C
12
X
12
+ … +
+ C
2m
X
2m
+ … + C
n1
X
n1
+ C
n2
X
n2
+ … + C
nm
X
nm
.
Данную целевую функцию следует минимизировать. Ограничения для скла-
дов компании имеют вид:
х
11
+ х
12
+ х
12
+ х
14
= 1000;
х
21
+ х
22
+ х
23
+ х
24
= 800;
х
31
+ х
32
+ х
33
+ х
34
= 2500.
Ограничения для покупателей:
х
11
+ х
21
+ х
31
= 1300; х
1
3
+ х
23
+ х
33
= 2700;
х
12
+ х
22
+ х
32
= 800; х
14
+ х
24
+ х
34
= 1700.
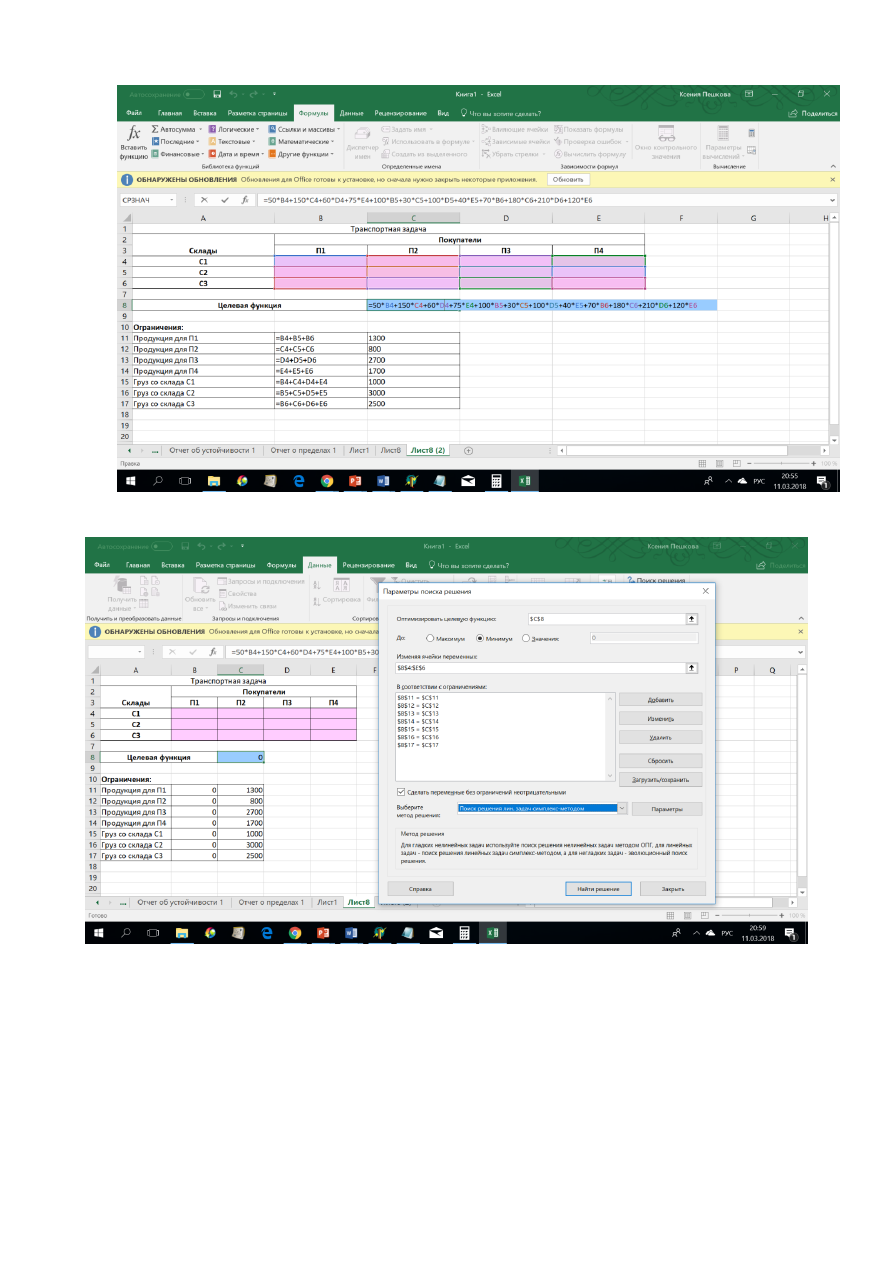
Создадим исходную таблицу в табличном процессоре. Матрица перевозок
содержит переменные решения, они пока пустые. Ограничения составляются ис-
ходя из потребностей покупателей и имеющихся запасов на складах.
18
Рис. 2.6. Исходная таблица с формулами
Рис. 2.7. Окно «Поиск решения»
19
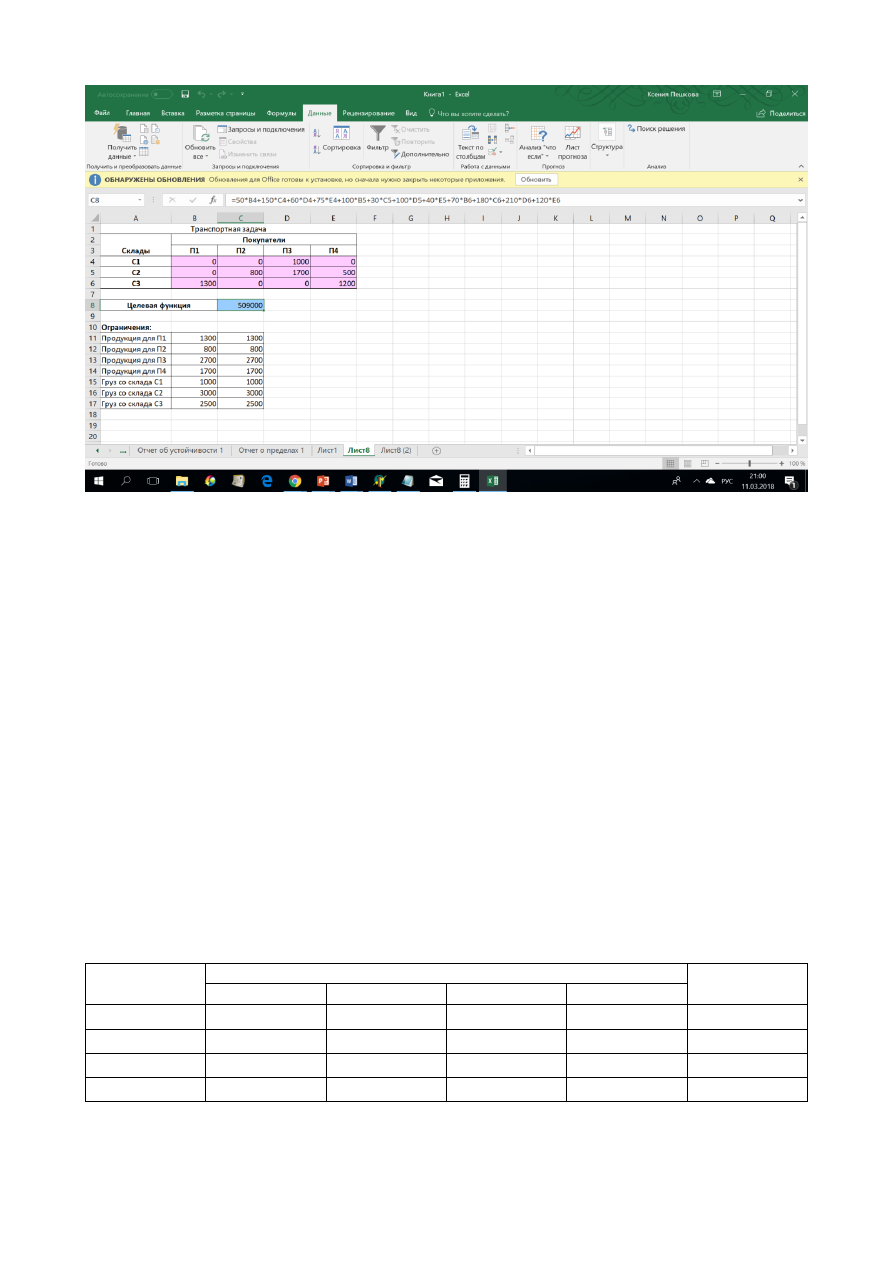
Рис. 2.8. Решение транспортной задачи
В соответствии с полученным решением со склада С1 компании надо перевезти
весь имеющийся там груз (в объеме 1000 штук) на склад покупателя П3. Со склада
С2 покупателю П2 – 800 шт., покупателю П3 – 1700 шт., покупателю П4 – 500 шт.
Со склада С3 покупателю П1 – 1300 шт., покупателю П 4 – 1200 шт. При этом ми-
нимальная стоимость всех перевозок составит 509 тыс. руб. (значение целевой
функции).
Задание для выполнения контрольной работы по вариантам. В этом зада-
нии вариант определяется по ПОСЛЕДНЕЙ цифре номера зачётной книжки, n –
номер варианта.
На складах поставщиков А1, А2, А3 имеются запасы грузов в количествах 70+n,
100+n и 80+n тонн соответственно. Грузополучатели В1, В2, В3, В4 должны полу-
чить эти товары в количествах 60+n, 40+n, 80+n и 70+n тонн соответственно. Тре-
буется найти такой вариант перевозки грузов, при котором сумма затрат на пере-
возки будет минимальной. Расходы по перевозке 1 тонны грузов в у.е. представ-
лены в таблице 2.17.
Таблица 2.17
Склад
Грузополучатели
Запасы
В1
В2
В3
В4
А1
5
2
3
4
70
+n
А2
4
3
2
0
100
+n
А3
0
2
2
1
80
+n
Потребность
60
+n
40
+n
80
+n
70
+n

20