ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Проектирование информационных систем
Добавлен: 21.10.2018
Просмотров: 10781
Скачиваний: 8

146
40.
Все
студенты
отвечают
на
последний
вопрос
не
-
правильно.
41.
Число
вопросов
таково,
что
размер
отчета
несколько
больше
одной
страницы.
42.
Число
вопросов
таково,
что
отчет
располагается
на
од-
ной
странице.
Опытный
программист,
вероятно,
согласится
с
той
точкой
зрения,
что
многие
из
этих
42-х
тестов
позволяют
выявить
на-
личие
общих
ошибок,
которые
могут
быть
сделаны
при
разра-
ботке
данной
программы.
Кроме
того,
большинство
этих
оши-
бок,
вероятно,
не
было
бы
обнаружено,
если
бы
использовался
метод
случайной
генерации
тестов
или
специальный
метод
ге-
нерации
тестов.
Анализ
граничных
значений,
если
он
применен
правильно,
является
одним
из
наиболее
полезных
методов
про-
ектирования
тестов.
Однако
он
часто
оказывается
неэффектив-
ным
из-за
того,
что внешне
выглядит
простым.
Необходимо
по-
нимать,
что
граничные
условия
могут
быть
едва
уловимы
и,
следовательно,
определение
их
связано
с
большими
трудностя-
ми.
6.4.4 Применение функциональных диаграмм
Одним
из
недостатков
анализа
граничных
значений
и
эк-
вивалентного
разбиения
является
то,
что
они
не
исследуют
комбинаций
входных
условий.
Например,
пусть
программа
MTEST
из
предыдущего
раздела
не
выполняется,
если
произве-
дение
числа
вопросов
и
числа
студентов
превышает
некоторый
предел
(например,
объем
памяти).
Такая
ошибка
не
обязательно
будет
обнаружена
тестированием
граничных
значений.
Тестирование
комбинаций
входных
условий
—
непростая
задача,
поскольку
даже
при
построенном
эквивалентном
раз-
биении
входных
условий
число
комбинаций
обычно
астроно-
мически
велико.
Если
нет
систематического
способа
выбора
подмножества
входных
условий,
то,
как
правило,
выбирается
произвольное
подмножество,
приводящее
к
неэффективному
тесту.
Метод
функциональных
диаграмм
или
диаграмм
причин-
но-следственных
связей
помогает
систематически
выбирать

147
тесты
с
высокой
результативностью.
Он
дает
полезный
побоч-
ный
эффект,
так
как
позволяет
обнаруживать
неполноту
и
не-
однозначность
исходных
спецификаций.
Функциональная
диаграмма
представляет
собой
формаль-
ный
язык,
на
который
транслируется
спецификация,
написанная
на
естественном
языке.
Диаграмме
можно
сопоставить
цифро-
вую
логическую
цепь
(комбинаторную
логическую
сеть),
но
для
ее
описания
используется
более
простая
нотация
(форма
запи-
си),
чем
обычная
форма
записи,
принятая
в
электронике.
Для
уяснения
метода
функциональных
диаграмм
вовсе
не
обяза-
тельно
знание
электроники,
но
желательно
понимание
булев-
ской
логики
(т.е.
логических
операторов
и,
или
и
не).
Построе-
ние
тестов
этим
методом
осуществляется
в
несколько
этапов.
1.
Спецификация
разбивается
на
«рабочие»
участки.
Это
связано
с
тем,
что
функциональные
диаграммы
стано-
вятся
слишком
громоздкими
при
применении
данного
метода
к
большим
спецификациям.
Например,
когда
тестируется
система
разделения
времени,
рабочим
уча-
стком
может
быть
спецификация
отдельной
команды.
При
тестировании
компилятора
в
качестве
рабочего
участка
можно
рассматривать
каждый
отдельный
опе-
ратор
языка
программирования.
2.
В
спецификации
определяются
причины
и
следствия.
Причина
есть
отдельное
входное
условие
или
класс
эк-
вивалентности
входных
условий.
Следствие
есть
вы-
ходное
условие
или
преобразование
системы
(остаточ-
ное
действие,
которое
входное
условие
оказывает
на
состояние
программы
или
системы).
Например,
если
сообщение
программе
приводит
к
обновлению
основ-
ного
файла,
то
изменение
в
нем
и
является
преобразо-
ванием
системы;
подтверждающее
сообщение
было
бы
выходным
условием.
Причины
и
следствие
определя-
ются
путем
последовательного
(слово
за
словом)
чте-
ния
спецификации.
При
этом
выделяются
слова
или
фразы,
которые
описывают
причины
и
следствия.
Ка-
ждым
причине
и
следствию
приписывается
отдельный
номер.
148
3.
Анализируется
семантическое
содержание
специфика-
ции,
которая
преобразуется
в
булевский
граф,
связы-
вающий
причины
и
следствия.
Это
и
есть
функцио-
нальная
диаграмма.
4.
Диаграмма
снабжается
примечаниями,
задающими
ог-
раничения
и
описывающими
комбинации
причин
и
(или)
следствий,
которые
являются
невозможными
из-
за
синтаксических
или
внешних
ограничений.
5.
Путем
методического
прослеживания
состояний
усло
-
вий
диаграммы
она
преобразуется
в
таблицу
решений
с
ограниченными
входами.
Каждый
столбец
таблицы
решений
соответствует
тесту.
6.
Столбцы
таблицы
решений
преобразуются
в
тесты.
Базовые
символы
для
записи
функциональных
диаграмм
показаны
на
рис.
6.9.
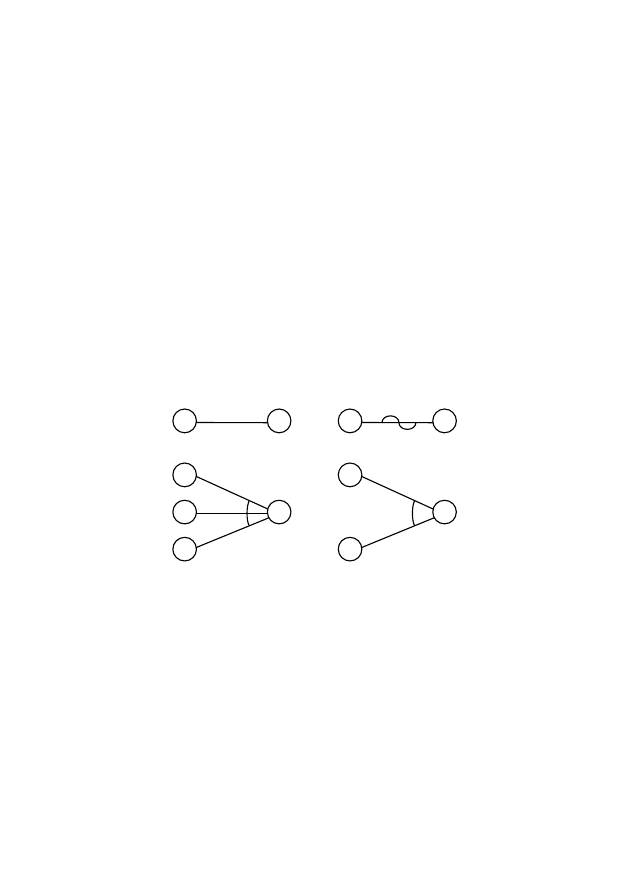
Рис.
6.9
—
Базовые
логические
отношения
функциональных
диаграмм
Каждый
узел
диаграммы
может
находиться
в
двух
со-
стояниях
—
0
или
1;
0
означает
состояние
«отсутствует»,
а
1
—
«присутствует».
Функция
тождество
устанавливает,
что
если
значение
a
есть
1,
то
и
значение
b
есть
1;
в
противном
случае
значение
b
есть
0.
Функция
не
устанавливает,
что
если
a
есть
1,
то
b
есть
0;
в
противном
случае
b
есть
1.
Функция
или
устанав-
ливает,
что
если
a,
или
b,
или
c
есть
1,
то
d
есть
1;
в
противном
случае
d
есть
0.
Функция
и
устанавливает,
что
если
d
и
b
есть
1,
a
b
Тождество
a
b
Не
b
Или
a
c
V
И
a
b
Λ
d
c
149
то
и
c
есть
1;
в
противном
случае
c
есть
0.
Последние
две
функ-
ции
разрешают
иметь
любое
число
входов.
Для
иллюстрации
изложенного
рассмотрим
диаграмму,
отображающую
спецификацию:
Символ
в
колонке
1
должен
быть
буквой
«А»
или
«В»,
а
в
колонке
2
—
цифрой.
В
этом
случае
файл
обновляется.
Если
первый
символ
неправильный,
то
выдается
сообщение
Х12,
а
если
второй
символ
неправильный
—
сообщение
X13.
Причинами
являются:
1
—
символ
«А»
в
колонке
1;
2
—
символ
«В»
в
колонке
1;
3
—
цифра
в
колонке
2,
а
следствиями
—
70
—
файл
обновляется;
71
—
выдается
сообщение
Х12;
72
—
выдается
сообщение
X13.
Функциональная
диаграмма
показана
на
рис.
6.10.
Отме-
тим,
что
здесь
создан
промежуточный
узел
11.
Рис.
6.10
—
Пример
функциональной
диаграммы
На
рис.
6.11
показана
эквивалентная
логическая
схема.
Рис.
6.11
—
Логическая
схема,
эквивалентная
диаграмме
на рис.
6.10
Хотя
диаграмма
отображает
спецификацию,
она
содержат
невозможную
комбинацию
причин
—
причины
1
и
2
не
могут
быть
установлены
в
1
одновременно.
В
большинстве
программ
определенные
комбинации
причин
невозможны
из-за
синтакси-
1
2
V
71
72
11
3
70
Λ
V
1
2
3
71
Λ
70
72
150
ческих
или
внешних
ограничений
(например,
символ
не
может
принимать
значения
«А»
и
«В»
одновременно).
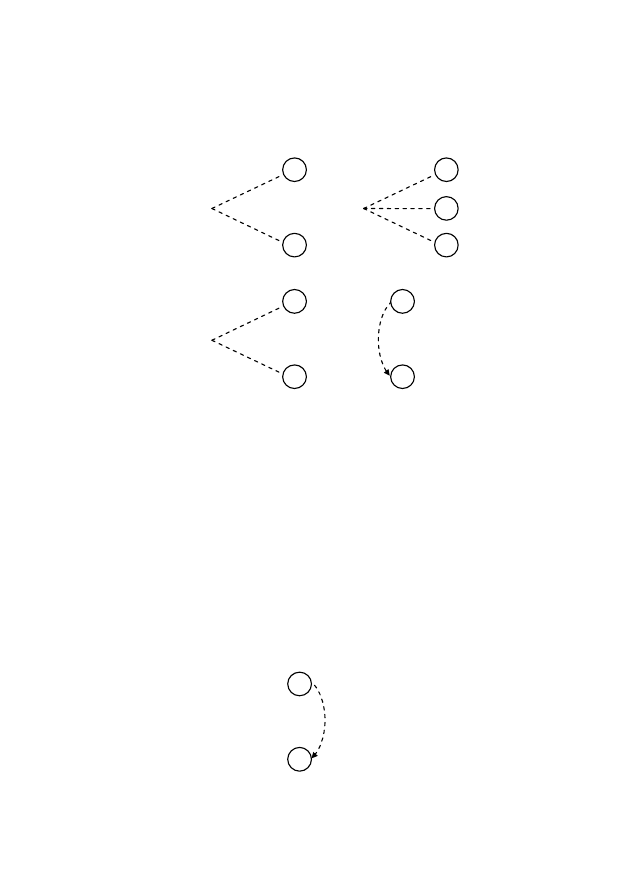
Рис.
6.12
—
Символы
ограничений
В
этом
случае
используются
дополнительные
логические
ограничения,
изображенные
на
рис.
6.12.
Ограничение
E
уста-
навливает,
что
E
должно
быть
истинным,
если
хотя
бы
одна
из
причин
—
a
или
b
—
принимает
значение
1
(a
и
b
не
могут
при-
нимать
значение
1
одновременно).
Ограничение
I
устанавлива-
ет,
что,
по
крайней
мере,
одна
из
величин
a,
b
или
c
всегда
должна
быть
равной
1
(a,
b
и
c
не
могут
принимать
значение
0
одновременно).
Ограничение
O
устанавливает,
что
одна
и
только
одна
из
величин
a
или
b
должна
быть
равна
1.
Ограни-
чение
R
устанавливает,
что
если
a
принимает
значение
1,
то
и
b
должно
быть
равно
1
(т.е.
невозможно,
чтобы
a
было
равно
1,
а
b
—
0).
Рис.
6.13
—
Символ
для
скрытого
ограничения
Исключает
a
b
E
Включает
a
c
b
I
Одно
и
только
одно
a
b
O
Требует
b
R
a
b
M
a