ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Проектирование информационных систем
Добавлен: 21.10.2018
Просмотров: 10779
Скачиваний: 8
156
Например,
причины
2
и
3
не
могут
присутствовать
без
причины
1.
Причина
4
не
может
присутствовать,
если
нет
при-
чин
2
и
3.
На
рис.
6.18
показана
окончательная
диаграмма
со
всеми
дополнительными
ограничениям.
Заметим,
что
может
присутствовать
только
одна
из
причин
5,
6,
7
или
8.
Другие
ог-
раничения
причин
являются
условиями
типа
«требует».
При-
чина
17
(много
строк
на
экране)
и
причина
8
(второй
операнд
отсутствует)
связаны
отношением
не;
причина
17
может
при-
сутствовать
только
в
отсутствии
причины
8.
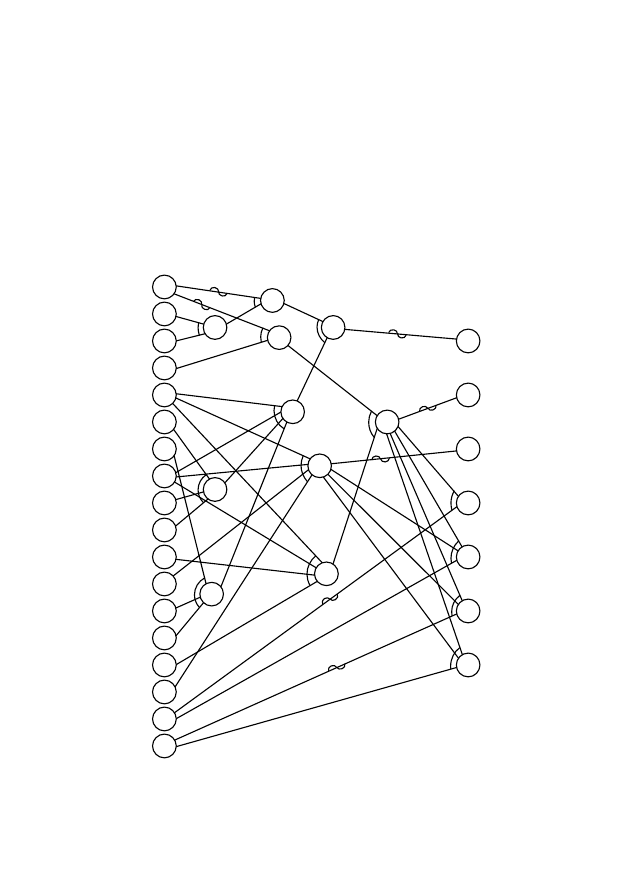
Рис.
6.17
—
Полная
функциональная
диаграмма
без
ограничений
31
32
36
35
33
34
38
39
40
92
93
91
94
95
96
97
37
V
Λ
V
Λ
V
Λ
Λ
Λ
V
V
Λ
Λ
Λ
Λ
1
2
3
4
9
10
12
16
13
14
17
18
15
11
6
7
8
5
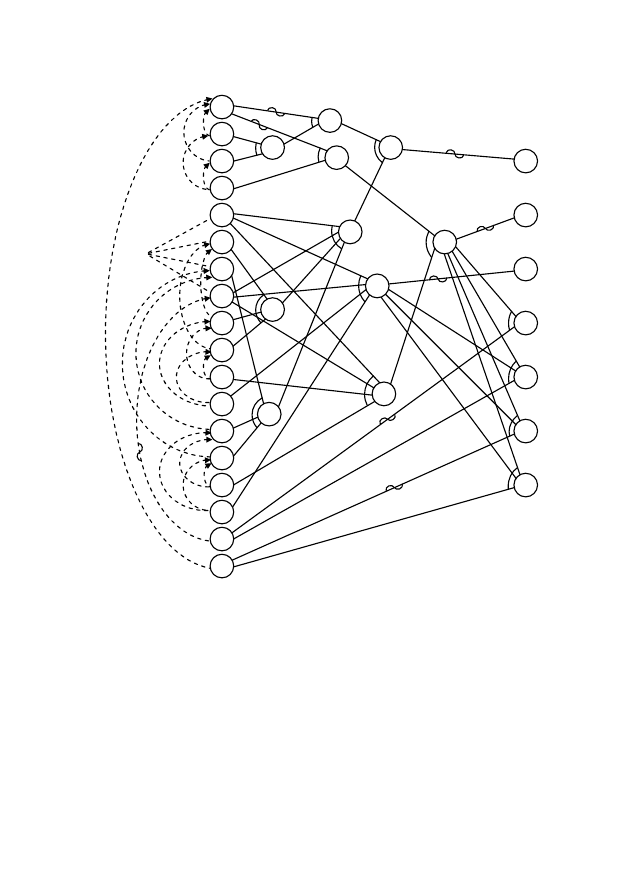
157
Рис.
6.18
—
Окончательная
функциональная
диаграмма
команды
DISPLAY
Третьим
шагом
является
генерация
таблицы
решений
с
ограниченными
входами.
В
таблице
решений
причины
есть
ус-
ловия,
а
следствия
есть
действия.
Процедура
генерации
заклю-
чается
в
следующем:
1.
Выбрать
некоторое
следствие,
которое
должно
быть
в
состоянии
1.
31
32
36
35
33
34
38
39
40
92
93
91
94
95
96
97
37
V
Λ
V
Λ
V
Λ
Λ
Λ
V
V
Λ
Λ
Λ
Λ
E
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
1
2
3
4
9
10
12
16
13
14
17
18
15
11
6
7
8
5

158
2.
Найти
все
комбинации
причин
(с
учетом
ограничений),
которые
установят
это
следствие
в
1,
прокладывая
из
этого
следствия
обратную
трассу
через
диаграмму.
3.
Построить
столбец
в
таблице
решений
для
каждой
комбинации
причин.
4.
Для
каждой
комбинации
причин
определить
состояния
всех
других
следствий
и
поместить
их
в
соответст-
вующий
столбец
таблицы
решений.
При
выполнении
этого
шага
необходимо
руководство
-
ваться
тремя
положениями:
1.
Если
обратная
трасса
прокладывается
через
узел
или,
выход
которого
должен
принимать
значение
1,
то
од-
новременно
не
следует
устанавливать
в
1
более
одного
входа
в
этот
узел.
Такое
ограничение
на
установку
входных
значений
называется
чувствительностью
пу-
ти.
Цель
данного
правила
—
избежать
пропуска
от-
дельных
ошибок
из-за
того,
что
одна
причина
маски-
руется
другой.
2.
Если
обратная
трасса
прокладывается
через
узел
и,
вы-
ход
которого
должен
принимать
значение
0,
то
все
комбинации
входов,
приводящие
выход
в
0,
должны
быть
перечислены.
Однако
когда
исследуется
ситуа-
ция,
где
один
вход
есть
0,
а
один
или
более
других
входов
есть
1,
не
обязательно
перечислять
все
условия,
при
которых
остальные
входы
могут
быть
1.
3.
Если
обратная
трасса
прокладывается
через
узел
и,
вы-
ход
которого
должен
принимать
значение
0,
то
необхо
-
димо
указать
лишь
одно
условие,
согласно
которому
все
входы
являются
нулями.
Когда
узел
и
находится
в
середине
графа
и
его
входы
исходят
из
других
проме-
жуточных
узлов,
может
существовать
чрезвычайно
большое
число
ситуаций,
при
которых
все
его
входы
принимают
значения
0.
Эти
положения
кратко
поясняются
рис.
6.19.
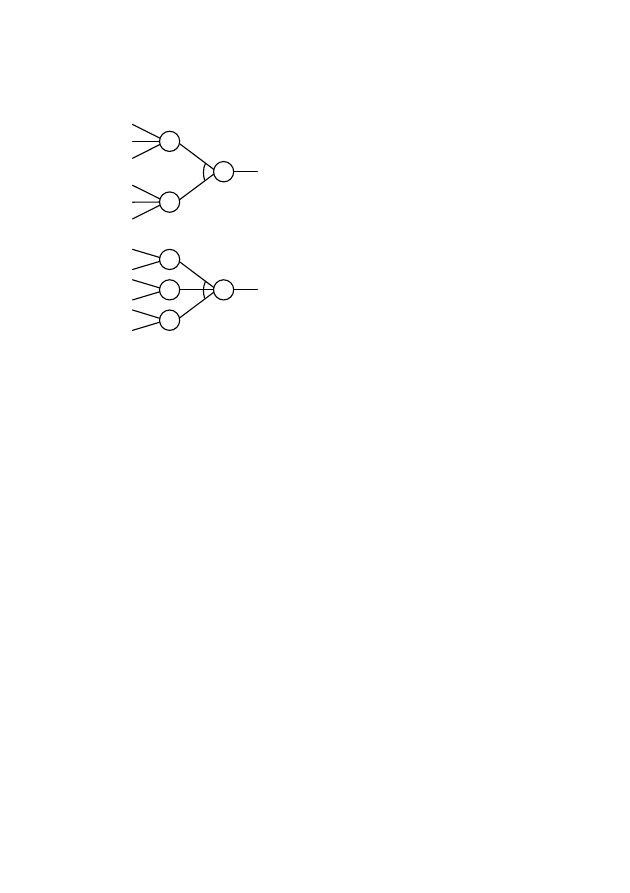
159
Рис.
6.19
—
Положения,
используемые
при
прокладке
обратной
трассы
через
диаграмму
Рис.
6.20
приведен
в
качестве
примера
функциональной
диаграммы.
Пусть
требуется
так
задать
входные
условия,
чтобы
установить
выходное
состояние
в
0.
Согласно
положению
3
следует
рассматривать
только
один
случай,
когда
узлы
5
и
6
—
нули.
По
положению
2,
для
состояния,
при
котором
узел
5
принимает
значение
1,
а
узел
6
—
значение
0,
следует
рас-
сматривать
только
один
случай,
когда
узел
5
принимает
значе-
ние
1
(не
перечисляя
другие
возможные
случаи,
когда
узел
5
может
принимать
значение
1).
Аналогично
для
состояния,
при
котором
узел
5
принимает
значение
0,
а
узел
6
—
значение
1,
следует
рассматривать
толь-
ко
один
случай,
когда
узел
6
принимает
значение
1
(хотя
в
дан-
ном
случае
он
является
единственным).
В
соответствии
с
поло-
жением
1,
если
узел
5
должен
быть
установлен
в
состояние
1,
то
не
рекомендуется
устанавливать
узлы
1
и
2
в
состояние
1
одновременно.
Таким
образом,
возможны
пять
состояний
узлов
1—4,
например
значения
0
0
0
0
(5
=
0,
6
=
0),
1
0
0
0
(5
=
1,
6
=
0),
1
0
0
1
(5
=
1,
6
=
0),
1
0
1
0
(5
=
1,
6
=
0),
0
0
1
1
(5
=
0,
6
=
1),
Ситуация
Состояние
1
2
3
4
a
b
x
a
c
x
b
V
Λ
1.
Если
X
должен
быть
равен
1,
то
не
следует
рассматривать
ситуацию,
где
a
=
b
=
1
(положение
1).
2.
Если
X
должен
быть
равен
0,
то
перечислить
все
ситуации,
где
a
=
b
=
0.
3.
Если
X
должен
быть
равен
1,
то
перечислить
все
ситуации,
где
a
=
b
=
=
c
=
1.
4.
Если
X
должен
быть
равен
0,
то
рассматриваем
только
одну
ситуацию,
где
a
=
b
=
c
=
0
(положение
3).
Для
состояний
a,
b
и
c
001,
010,
100,
011,
101
и
110
рассмотреть
только
одну,
любую
из
этих
ситуаций
(поло-
жение
2).
160
а
не
13,
которые
приводят
к
выходному
состоянию
0.
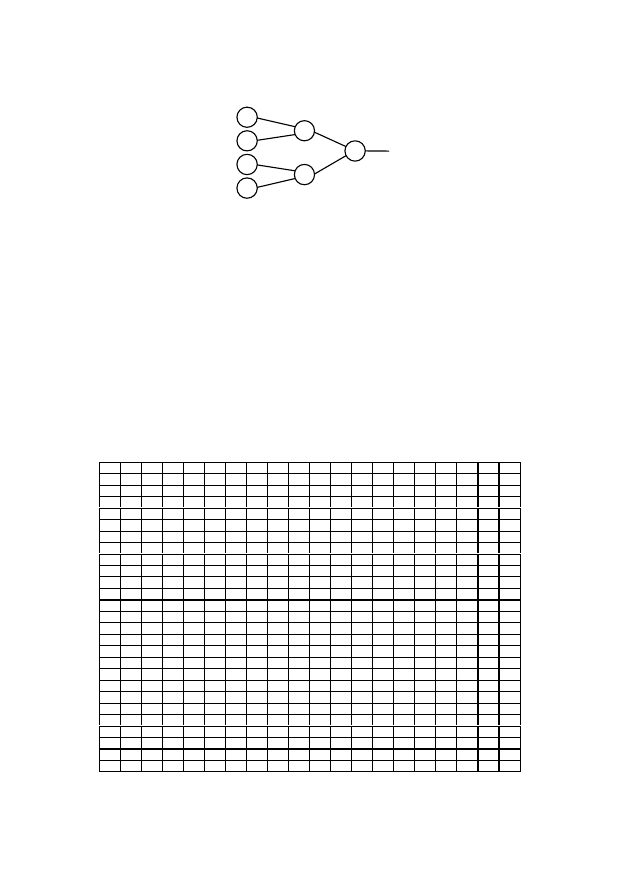
Рис.
6.20
—
Пример
функциональной
диаграммы
для
иллюстрации
обратной
трассировки
На
первый
взгляд,
эти
положения
могут
показаться
не-
объективными,
но
они
преследуют
важную
цель:
уменьшить
комбинаторику
диаграммы.
Их
применение
позволяет
избежать
ситуаций,
которые
приводят
к
получению
малорезультативных
тестов.
Если
не
исключать
малорезультативные
тесты,
то
общее
число
тестов,
порождаемых
по
большой
функциональной
диа-
грамме,
получается
астрономическим.
Если
же
и
без
них
число
тестов
все
еще
оказывается
большим,
то
выбирается
некоторое
подмножество
тестов,
при
этом
не
гарантируется,
что
малоре
-
зультативные
тесты
будут
исключены.
Поэтому
самое
лучшее
—
исключить
их
в
процессе
анализа
диаграммы.
Рис.
6.21
—
Первая
половина
результирующей
таблицы
решений
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
1
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
3
0
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
4
1
1
0
0
1
1
1
1
5
0
1
1
6
1
1
1
0
1
1
1
1
1
1
1
7
0
1
1
1
1
1
8
0
1
9
1
1
1
1
0
0
0
1
1
1
10
1
1
1
0
1
0
1
1
1
1
11
0
0
1
12
0
13
1
0
0
1
1
14
0
1
0
1
1
15
0
0
16
17
0
0
18
1
1
91
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
92
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
93
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
94
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
95
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
96
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
97
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Λ
1
5
6
7
2
3
4
V
V