ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Проектирование информационных систем
Добавлен: 21.10.2018
Просмотров: 10775
Скачиваний: 8

171
алгоритмы
не
равнозначны
по
сложности.
Модифицированный
алгоритм
—
двоичный
поиск
—
имеет
вид:
−
проверить
первый
элемент;
−
if
заданный
элемент
не
найден,
then
продолжить
поиск
в
верхней
или
нижней
половине
списка.
В
этом
случае
задача
разбивается
на
две
части,
примерно
одинаковые
по
сложности.
Каждая
из
частей
может
иметь
ре-
курсивное
решение.
7.3
Рекурсия
и
динамическое
программирование
7.3.1 Рекурсия
Иногда
возможно
сформулировать
решение
задачи
как
известное
преобразование
другого,
более
простого,
варианта
той
же
задачи.
Если
этот
процесс
продолжить
до
тех
пор,
пока
не
получится
нужное
значение,
то
подобное
решение
называет-
ся
рекурсивным.
Примером
рекурсивного
решения
является
вычисление
факториала
fact(N) = 1×2×…×N.
Пусть
неизвестно
значение
fact(460),
если
умножить
fact(459)
на
460,
тогда
задача
сводит-
ся
к
вычислению
fact(459).
Если
это
преобразование
далее
по-
вторить
458
раз,
то
можно
вычислить
значение
факториала,
по-
скольку
fact(1) = 1.
Таким
образом,
функция
F
является
рекур-
сивной,
если:
1)
F(N) = G(N, F(N – 1))
для
некоторой
известной
функ-
ции
G
и
2)
F(1)
равно
некоторому
известному
значению.
Функция
F
может
быть
функцией
нескольких
параметров.
Значение
N
должно
быть
задано
в
явном
виде.
Величина
N
мо-
жет
быть
элементом
во
множестве,
длиной
интервала
или
неко-
торым
другим
параметром.
Рекурсивное
решение
всегда
записывается
проще,
чем
со-
ответствующий
нерекурсивный
вариант.
Относительно
скоро-
сти
решения
однозначных
выводов
сделать
нельзя.
Это
зависит
от
сложности
функции
G.

172
7.3.2 Динамическое программирование
Динамическое
программирование
—
это
табличный
ме-
тод,
при
котором
используется
одна
и
та
же
схема
вычисления
всех
подзадач
данной
задачи.
При
использовании
этого
метода
однажды
найденный
результат
записывается
в
таблицу
и
далее
повторно
не
вычисляется.
7.3.3 Моделирование
Часто
бывает
невозможно
получить
точное
решение
зада-
чи
по
соображениям
стоимости,
сложности
или
размера.
Такие
ситуации
возникают
при
решении
задач
по
управлению
движе-
нием,
экономическому
прогнозированию
и
др.
В
этих
случаях
строится
представление
определенных
свойств
задачи,
назы-
ваемой
моделью,
а
все
другие
свойства
не
учитываются.
При
этом
проводится
анализ
поведения
нужных
свойств
модели.
Такой
подход
называется
моделированием.
Моделирование
применяется
во
многих
областях,
однако
при
разработке
про-
граммного
обеспечения
моделирование
используется
достаточ-
но
редко.
В
основном
моделирование
используется
при
иссле-
довании
на
ЭВМ
различных
физических
процессов,
особенно
когда
известно
математическое
описание
последних.
Тем
не
ме-
нее
данный
подход
заслуживает
пристального
внимания
про-
граммистов
при
разработке
больших
программных
комплексов.
7.4
Поиск
Поиск
—
это
процесс
нахождения
нужных
значений
в
не-
котором
множестве.
Семейство
элементов
может
быть
структури-
рованным
либо
нет.
Если
оно
не
структурировано,
поиск
обычно
означает
нахождение
нужного
элемента
в
списке.
Если
семейство
элементов
структурировано
(дерево,
граф
и
др.),
то
под
поиском
понимают
нахождение
правильного
пути
в
структуре.
Обычно
каждый
элемент
имеет
три
компонента:
−
ключ
—
это
элемент,
используемый
для
доступа
к
дан-
ным
(он
может
быть
именем
в
справочнике,
словом
в
индексе
или
названием
раздела
в
таблице);

173
−
аргумент
—
это
числа,
связанные
с
элементом
(адрес,
номер
телефона
и
др.);
−
структуру
—
это
дополнительная
информация,
прини-
маемая
для
описания
данных,
такая,
как
адрес
сле-
дующего
элемента
в
семействе
и
т.п.
7.4.1 Поиск в списках
Данный
поиск
проводится
четырьмя
различными
спосо-
бами:
прямым,
линейным,
двоичным
и
хешированием.
Прямой
поиск.
При
прямом
поиске
местоположение
эле-
мента
определяется
непосредственно
с
помощью
ключа
(комна-
та
в
здании).
Прямой
поиск
применяется
тогда,
когда
число
элементов
фиксировано
и
их
сравнительно
немного.
Линейный
поиск.
Данный
вид
поиска
наиболее
простой
для
программной
реализации,
хотя
его
выполнение
занимает
много
времени.
Элементы
проверяются
последовательно,
по
одному,
пока
нужный
элемент
не
будет
найден.
В
отличие
от
прямого
поиска
здесь
нет
системы
в
расположении
элементов.
Если
список
содержит
N
элементов,
то
каждый
раз
в
среднем
будут
проверяться
N/2
элементов.
Линейный
поиск
медленный,
но
позволяет
легко
добавлять
новые
элементы,
помещая
их
в
конец
списка.
Хорошо
разработанная
программа
обычно
имеет
простую
(линейную)
структуру,
и,
следовательно,
такую
же
структуру
должны
иметь
и
данные,
поэтому
линейный
поиск
в
таких
структурах
эффективен.
Двоичный
поиск.
Для
ведения
двоичного
поиска
ключи
должны
быть
упорядочены
по
величине
или
алфавиту.
В
этом
случае
можно
добиться
среднего
времени
поиска
log
2
N.
При
двоичном
поиске
ключ
сравнивается
с
ключом
среднего
эле-
мента
списка.
Если
значение
ключа
больше,
то
та
же
самая
процедура
повторятся
для
второй
половины
списка,
если
же
меньше,
то
для
первой.
Таким
образом,
за
шаг
этого
процесса
список
уменьшается
наполовину.
Основная
трудность
при
двоичном
поиске
—
как
вводить
новые
элементы.
Так
как
список
упорядочивается,
то
введение
нового
элемента
может
вызвать
переписывание
всех
элементов
для
того,
чтобы
новый
элемент
поместить
в
нужном
месте.

174
Хеш-поиск.
Этот
вид
поиска
является
попыткой
приме-
нить
прямой
поиск
для
поиска
в
больших
наборах
данных.
Из
изначального
значения
ключа
вычисляется
значение
псевдо-
ключа,
называемого
хеш-кодом,
и
этот
код
используется
как
индекс
в
таблице
адресов
элементов.
Если
все
ключи
соответст-
вуют
разным
хеш-кодам,
то
любой
элемент
будет
найден
за
один
прямой
поиск.
Пример.
В
абстрактном
компиляторе
может
быть
отведе-
но
1000
мест
для
имен
переменных.
В
языке
допускаются
сло-
ва
из
6
символов.
Это
позволяет
создавать
26
6
имен,
что
гораздо
больше,
чем
размер
таблицы
символов.
Но
если
каждое
число,
представляющее
имя,
уменьшить
до
числа,
находящегося
меж-
ду
0
и
999,
то
имена
могут
быть
записаны
в
таблицу.
Алгорит-
мы
вычисления
хеш-кодов
различны,
например
имя
(ключ)
можно
рассматривать
как
двоичное
число.
Это
число
можно
разделить
на
размер
таблицы,
остаток
использовать
как
код.
Другие
алгоритмы
предлагают
сложение
битов
внутри
числа
или
некоторые
другие
функции
с
ключом.
Недостатком
хеш-поиска
является
тот
факт,
что
некото-
рые
идентификаторы
могут
иметь
одинаковые
хеш-коды,
по-
этому
возникает
проблема
обработки
пересечений
элементов,
т.е.
элементов,
имеющих
одинаковые
хеш-коды.
Когда
опреде-
ленное
значение
хеш-кода
встречается
первый
раз,
его
поме-
щают
в
определенное
место
в
таблице.
Если
произошло
пересе-
чение
с
другим
элементом,
его
помещают
в
другое
место
в
со-
ответствии
со
следующим
алгоритмом:
INSERT: procedure (
ключ, аргумент);
declare
1 TABLE(
размер),
2 KEY,
2 ARGUMENT;
declare
хеш–код;
Вычислить хеш–код;
/*
если запись находится в таблице */
if
TABLE(
хеш-код).KEY = ключ then return;
/*
обработка совпадающих хеш-кодов */
do while
(TABLE(
хеш-код).KEY
≠0 &
TABLE(
хеш-код).KEY
≠ключ);
хеш–код = новое значение, зависящее от
175
(
хеш–код, ключ);
end
;
TABLE(
хеш-код).KEY = ключ;
TABLE(
хеш-код).ARGUMENT = аргумент;
end
INSERT;
Таким
образом,
в
случае
пересечения
элементов
имеется
переход
к
следующему
месту
в
таблице.
Если
нужное
место
занято,
—
то
переход
на
место,
расположенное
на
некотором
расстоянии
от
занятого,
или
вычисление
нового
хеш-кода,
ис-
ходя
из
имеющегося
ключа
и
кода.
Основным
недостатком
хеш-поиска
является
тот
факт,
что
при
плотном
заполнении
таблицы
алгоритм
ввода
элемен-
тов
весьма
трудоемок.
7.4.2 Деревья поиска
Если
данные
организованы
как
структура
дерева,
алго-
ритм
поиска
сводится
к
алгоритму,
просматривающему
все
уз-
лы
дерева.
Для
ведения
поиска
существуют
два
основных
алго-
ритма
поиска:
поиск
в
глубину
и
поиск
в
ширину.
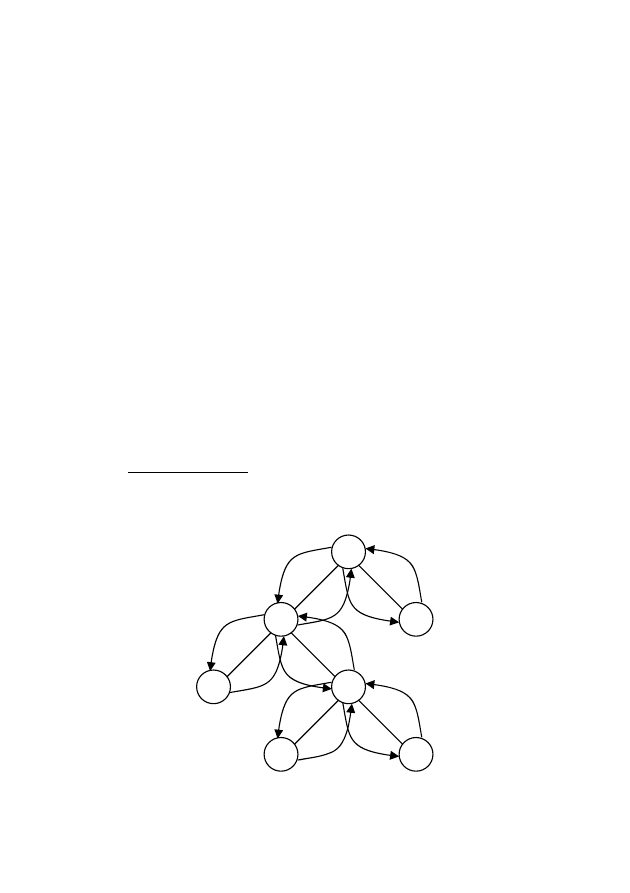
Поиск
в
глубину.
При
поиске
в
глубину
каждая
ветвь
де-
рева
просматривается
слева
направо.
Для
двоичных
деревьев
алгоритм
поиска
имеет
простую
рекурсивную
структуру
(рис.
7.1):
Рис.
7.1
—
Схема
поиска
по
двоичному
дереву
A
B
G
C
D
E
F