Файл: Технология раработки програмного обеспечения УП.pdf

176 

DEPTHFIRST: procedure(TREE); 
  declare 1 TREE, 
            2 KEY, 
            2 ARGUMENT, /* 

данные */ 

            2 RightSon, /* 

ноль, если нет сына*/ 

            2 LeftSon;  /* 

ноль, если нет сына */ 

  if TREE = null then return; 
  if 

текущий узел не KEY then do; 

    call DEPTHFIRST(LtftSon); 
    call DEPTHFIRST(RightSon); 
  end; 
end

 DEPTHFIRST; 

Заметим,

что

если

дерево

упорядочено

таким

образом,

что

LeftSon

имеет

ключ,

величина

которого

меньше,

чем

значе-

ние

корневого

узла,

а

величина

ключа

для

RightSon

больше,

чем

значение

корневого

узла,

то

такой

алгоритм

аналогичен

алгоритму

двоичного

поиска.

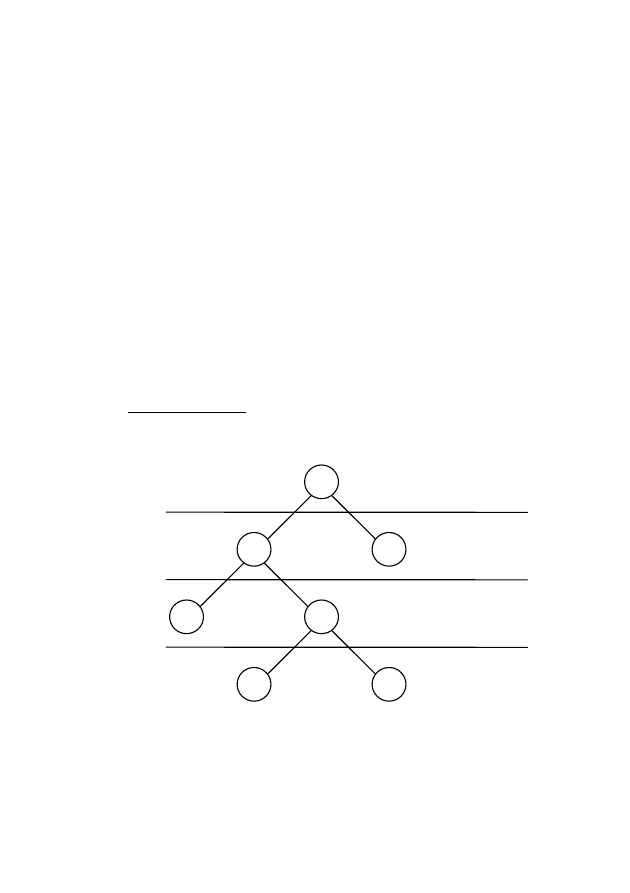
Поиск

в

ширину.

Это

алгоритм

поиска,

при

котором

про-

сматривается

каждый

уровень

в

направлении

сверху

вниз

(рис.

7.2).

Рис.

7.2

—

Поиск

в

ширину

A

B

G

C

D

E

F

{

A

} 

{

B,

G

} 

{

C,

D

} 

{

E,

F

} 

177 

При

таком

алгоритме

параллельного

поиска

быстро

нахо-

дятся

кратчайшие

ветви

дерева.

В

общем

виде

алгоритм

имеет

структуру:

BREADTHFIRST: procedure(solution); 
  declare 1 TREE, 
            2 ARGUMENT, /* 

данные */ 

            2 SONS(N);  /* 

произвольные деревья */ 

  declare (solution, NextStep) set of TREE; 
  /* 

переход вниз для каждого уровня */ 

  do while (solution 

≠ 0); 

    NextStep = {TREE.SONS(I) 

для всех I и TREE 

в solution}; 

    call BREADTHFIRST(NextStep); 
  end; 
end

 BREADTHFIRST; 

Поиск

в

ширину

очень

популярен

при

решении

задачи

о

лабиринте.

Поиск

с

возвратом.

Для

многих

алгоритмов

часто

требу-

ется

перебор

возможных

вариантов

решения

задачи.

Один

из

таких

способов

перебора

называется

поиском

с

возвратом.

Алгоритм:

Вызвать первую часть; 
do while

 (

не окончится); 

вызвать следующую часть; 

  do while (

нет возможности продолжить); 

Вернуться на предыдущий уровень; 

Проверить возможность альтернативного решения 

для этого уровня; 

  end; 
end

; 

Алгоритм

поиска

в

глубину

является

примером

поиска

с

возвратом:

Начать

с

корневого

узла;

do while

 (

существуют не просмотренные узлы); 

Перейти к узлу «левый сын», если возможно; 

Иначе перейти к узлу «правый брат»; 

  do while (

нет узлов «левый сын» и «правый брат); 

Перейти к узлу «отец»; 

Перейти к узлу «правый брат», если можно; 

  end; 
end

; 

178 

7.4.3 Стратегия распределения памяти 

Одним

из

типов

поиска

являются

задачи

по

распределе-

нию

памяти

(наиболее

характерны

они

при

создании

ОС),

одна-

ко

во

многих

прикладных

алгоритмах

эти

задачи

возникают

при

создании

прикладных

программ,

работающих

с

большим

объе-

мом

данных.

Если

до

начала

обработки

полный

объем

данных,

которые

подлежат

обработке,

неизвестен,

то

используется

об-

щий

подход

для

распределения

областей

этой

памяти

согласно

заданным

требованиям.

Дана

фиксированная

область

памяти,

задача

заключается

в

том,

чтобы

занимать

и

освобождать

меньшие

области

памяти

большой

областью,

без

выхода

за

границы

памяти.

При

распре-

делении

памяти

проверяются

наибольшие

свободные

области.

Обычно

эти

области

малы

для

размещения

в

них

всех

данных,

и,

следовательно,

память

становится

фрагментной.

Имеются

следующие

способы

уменьшения

фрагментности.

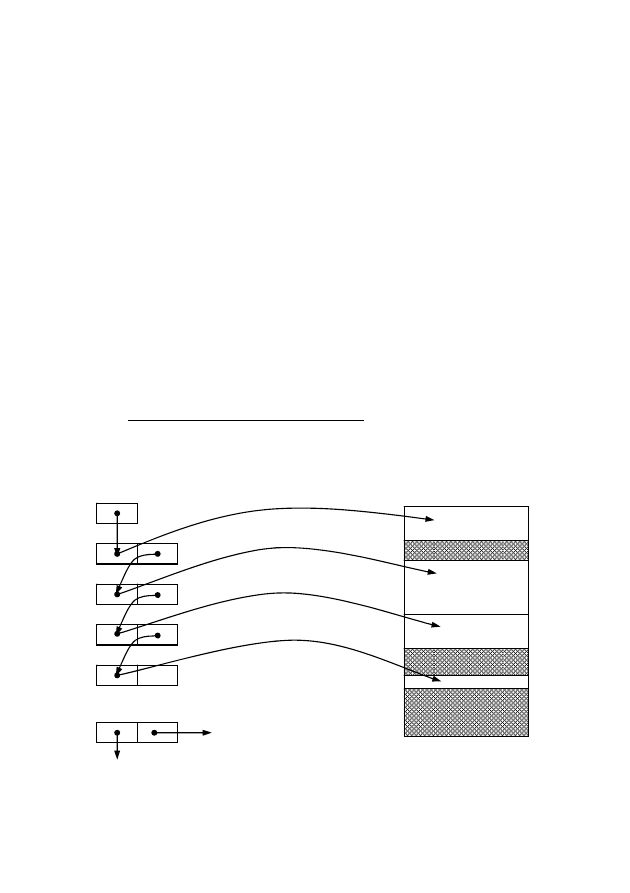
Первое

возможное

размещение.

Последовательно

про-

сматриваются

области

памяти,

пока

не

найдется

первая,

доста-

точная

для

размещения.

Вся

область

организована

в

список

и

упорядочена

по

адресам

(рис.

7.3).

Рис.

7.3

—

Схема

распределения

памяти

Список

свободных

областей

памяти

… 

Следующий

элемент

в

списке

Адрес

текущего

элемента

Память

179 

Поиск

в

этом

списке

осуществляется

последовательно

до

тех

пор,

пока

не

будет

найдена

достаточно

большая

область

для

размещения

данных.

Тогда

эта

область

изымается

из

списка,

а

на

это

место

помещается

меньшая

свободная

область

—

остав-

шаяся

незанятая

часть

исключенной

области.

С

помощью

этого

метода

легко

освобождать

ранее

занятые

области

памяти.

С

этой

целью

просматривается

список,

как

только

он

будет

упо-

рядочен

по

адресам,

то

нетрудно

найти

место,

чтобы

пометить

освобожденную

область

памяти.

Соседние

адреса

—

смежные

в

списке,

поэтому

легко

объединить

две

свободные

области

в

од-

ну,

большую

по

размеру.

Данный

способ

самый

простой,

однако

поскольку

занятие

области

памяти

осуществляется

после

нахождения

первой

об-

ласти,

достаточной

для

размещения

данных,

память

становится

фрагментной.

Наилучшее

размещение.

Последовательно

просматрива-

ются

все

области,

выбирается

наименьшая

область,

размер

ко-

торой

больше

или

равен

требуемому

объему

для

размещения

данных.

В

этом

случае

области

связываются

друг

с

другом

по

размеру,

а

не

по

адресам.

Алгоритм

размещения-освобождения

аналогичен

первому

возможному

размещению.

Однако

в

этом

случае

стратегия

размещения

приводит

к

меньшей

фрагмент

-

ности,

потому

что

используется

область

наименьшего

размера

для

размещения

данных.

Однако

так

как

свободная

область

не

упоря-

дочена

по

адресам,

алгоритм

объединения

двух

свободных

облас-

тей

в

область

большего

объема

довольно

сложен.

Сопрягаемые

области

памяти.

Областями

памяти

являют-

ся

N

цепочек

размером

2

N

каждая.

Если

область

размером

2

K

от-

сутствует,

а

имеется

свободная

область

размером

2

K+1

,

то

она

раз-

бивается

на

две

сопрягаемые

области

размером

2

K

.

После

того

как

области

освободятся,

они

рассматриваются

как

области

размером

2

K

,

которые

можно

объединить

в

область

размером

2

K+1

.

7.5 

Сортировка

Сортировка

—

это

процесс

размещения

элементов

в

спи-

ске

в

некоторой

числовой

или

лексикографической

последова-

тельности

(порядке).

Различаются

следующие

виды

сортировки.

180 

Обменная

сортировка.

При

этом

способе

наименьший

эле-

мент

выдвигается

в

начало

списка,

следующий

по

величине

—

на

вторую

позицию

и

т.д.

Для

списка

N

элементов

производится

N(N – 1)/2,

т.е.

O(N

2

)

операций.

Естественно,

что

для

больших

значений

N использование

этой

сортировки

нецелесообразно.

Алгоритм:

EXCHANGE_SORT procedure(LIST,N); 
  declare LIST(N); /* 

массив сортировки */ 

  do I=1 to N-1; 
    do J=I+1 to N; 
      if LIST(J)< LIST(I) then 
        Reverse(LIST(J), LIST(I)); 
    end; 
  end; 
end

 EXCHANGE_SORT; 

Сортировка

слиянием.

Данный

способ

сортировки

схож

с

методом

разбиения

на

подзадачи.

Вначале

неотсортированный

список

делится

на

две

части,

затем

каждая

часть

сортируется

независимо.

После

этого

списки

объединяются.

Алгоритм:

MERGE_SORT procedure(LIST,N); 
  declare

 LIST(N); /* 

массив сортировки */ 

  call

 MERGE_SORT(LIST(1:N/2),N/2, 

    (LIST(N/2+1:N),N/2)); 
  /* 

объединение отсортированных списков */ 

end

 MERGE_SORT; 

Процедура

слияния

отсортированных

списков

размером

K

выполняется

за

2×K

операций

путем

просмотра

первого

элемен-

та

в

каждом

списке

и

перенесения

меньшего

из

двух

в

новый

список.

Эти

два

действия

повторяются

для

каждого

из

2×K

эле-

ментов

списка,

получается

4×K

операций.

Так

как

каждый

из

списков

уже

отсортирован,

нужно

проверить

только

первые

элементы.

Хотя

для

реализации

этого

способа

нужна

память

большого

объема,

время

сортировки

путем

последовательного

разбиения

каждого

из

подсписков

на

два

можно

уменьшить

до

величины

2

log

.

N

N