Добавлен: 21.10.2018
Просмотров: 1664
Скачиваний: 54
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
ИНСТИТУТ ЭКОНОМИКИ И УПРАВЛЕНИЯ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ И ИНФОРМАТИКИ
Отчёт по лабораторной работе
на тему: «Решение задач оптимизации
средствами Microsoft Excel»
Вариант 1.
Выполнил студент
гр. 060802-21 Э. Долыев
Проверил
к. ю. н., доцент А. А. Мухин
Ижевск, 2011 г
Исходная постановка задачи
Кондитерская фабрика для производства трёх видов карамели А, В, С использует три вида основного сырья: сахарный песок, патоку, фруктовое пюре. Нормы расхода сырья каждого вида на производство 1 тонны карамели данного вида приведены в таблице.
|
Вид сырья |
Норма расхода (т) на 1 т карамели |
Общее количество сырья (т) |
||
|
А |
В |
С |
||
|
Сахарный песок |
0,8 |
0,5 |
0,6 |
800 |
|
Патока |
0,4 |
0,4 |
0,3 |
600 |
|
Фруктовое пюре |
- |
0,1 |
0,1 |
120 |
|
Прибыль (руб.) |
108 |
112 |
126 |
|
Найти план производства карамели, обеспечивающей максимальную прибыль.
Формальная постановка задачи
Обозначим через X производство карамели вида А, через Y – производство карамели вида В, через Z - производство карамели вида С. Требуется найти наилучшие для фабрики значения X, Y, Z. Наилучшими для данной задачи являются такие значения, которые максимизируют прибыль:
Р= 108 X + 112 Y + 126 Z → max
Поскольку X, Y, Z выражают производство карамели, то они не могут быть отрицательны, т. е.
X ≥ 0, Y ≥ 0, Z ≥ 0.
Ограничения на общее количество сырья могут быть записаны следующим образом:
0,8X + 0,5Y + 0,6Z ≤ 800 (для сахарного песка),
0,4X + 0,4Y +0,3Z ≤600 (для патоки),
0,1Y + 0,1Z ≤ 120 (для фруктового пюре).
Таким образом, задача состоит в том, чтобы найти значения X, Y, Z, удовлетворяющие условиям:
X ≥ 0, Y ≥ 0, Z ≥ 0,
0,8X + 0,5Y + 0,6Z ≤ 800,
0,4X + 0,4Y +0,3Z ≤600,
0,1Y + 0,1Z ≤ 120
и максимизирующими функцию Р= 108 X + 112 Y + 126 Z.
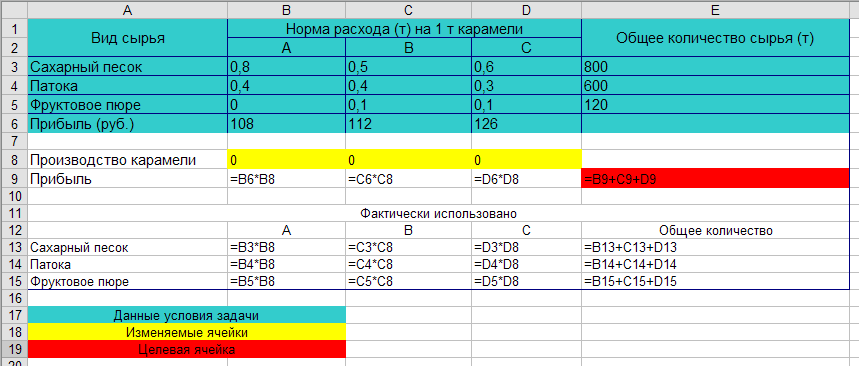
Ячейки B8:D8 –производство карамели вида А, В, С.
В ячейке E9 находится функция, максимизирующая прибыль от производства карамели трёх видов А, В, С. В ячейках B9, C9 и D9 соответственно находятся формулы, которые вычисляют прибыль по каждому виду карамели.
В ячейках B13, C13 и D13 идёт расчёт фактически затраченного сахарного песка для производства карамели вида А, В, С, в ячейке E13 – общее количество затраченного сахарного песка.
В ячейках B14, C14 и D14 идёт расчёт фактически затраченной патоки для производства карамели вида А, В, С, в ячейке E14 – общее количество затраченной патоки.
В ячейках B15, C15 и D15 идёт расчёт фактически затраченного фруктового пюре для производства карамели вида А, В, С, в ячейке E15 – общее количество затраченного фруктового пюре.
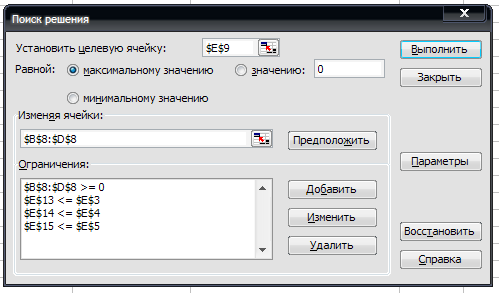
Таким образом, заполняем диалоговое окно Поиск решения:
В поле установить целевую указываем ячейку, содержащую оптимизируемое значение (Е9), устанавливаем переключатель равной максимальному значению.
В поле Изменяя ячейки задаём диапазон подбираемых параметров – B8:D8.
Набор ограничений:
-
B8:D8 ≥ 0 (производство карамели не может быть отрицательным);
-
E13 ≤ E3 (ограничение на количество сахарного песка );
-
E14 ≤ E4 (ограничение на количество патоки);
-
E15 ≤ E5(ограничение на количество фруктового пюре).
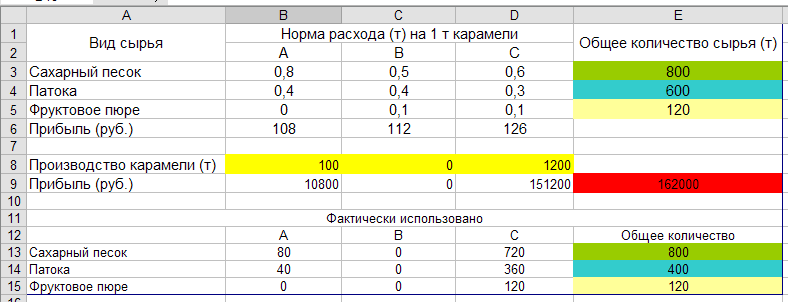
Анализ найденного решения
Таким образом, наилучшими для данной задачи являются 100 т карамели вида А, 1200 т карамели вида С, а производство карамели вида В при данных условиях является невыгодным, поэтому её выпуск равен 0. При таком выпуске продукции фактически затраченное количество сырья не превышает планируемого объёма. И при этом прибыль кондитерской фабрики будет достигать своего максимума, равного 162 000 рублей.