Лабораторная работа №1

МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Пусть дано нелинейное уравнение вида:

, (1)

где - функция, определенная и непрерывная на некотором промежутке. Требуется найти корни уравнения, которые при подстановке в данное уравнение превращают его в числовое равенство.

Для решения данных уравнений применяют численные методы, которые являются приближенными с заданной степенью точности и состоят из двух этапов:

1. Находятся отрезки , внутри которых содержится один корень . Этот этап называется отделением корней или локализацией корней. По сути, на данном этапе осуществляется грубое нахождение корней .

2. Грубое значение каждого корня уточняется до заданной точности одним из численных методов, в которых реализуется последовательные приближения.

1. Метод деления отрезка пополам (метод бисекции)

Допустим, что нам удалось найти отрезок [а,b], на котором расположено искомое значение корня х=с, т. е. с ϵ [а,b]. В качестве начального приближения корня с₀ принимаем середину этого отрезка:

Далее исследуем значения функции F(x) на концах отрезков [а, с_о] и [с_о,b], т.е. в точках а, с_о, b. Тот из отрезков, на концах которого F(x) принимает значения разных знаков, содержит искомый корень; Допустим, что нам удалось найти отрезок [а,b], на котором расположено искомое значение корня поэтому его принимаем в качестве нового отрезка [a₁,b₁]. Вторую половину отрезка [а,b], на которой знак F(x) не меняется, отбрасываем. В качестве первого приближения корня принимаем середину нового отрезка

и т. д.

Таким образом, k-е приближение вычисляется как

После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после k - итераций он сокращается в 2к раз:

Иллюстрация данного метода приведена на рисунке 1.

Процесс вычислений завершается, когда длина текущего интервала становится меньше заданной величины точности - нахождения корня.

Рисунок 1 Графическая интерпретация нахождения корней

функции методом бисекции

Пример

Методом половинного деления уточнить корень уравнения лежащий на отрезке  0, 1с точностью до 0,001.

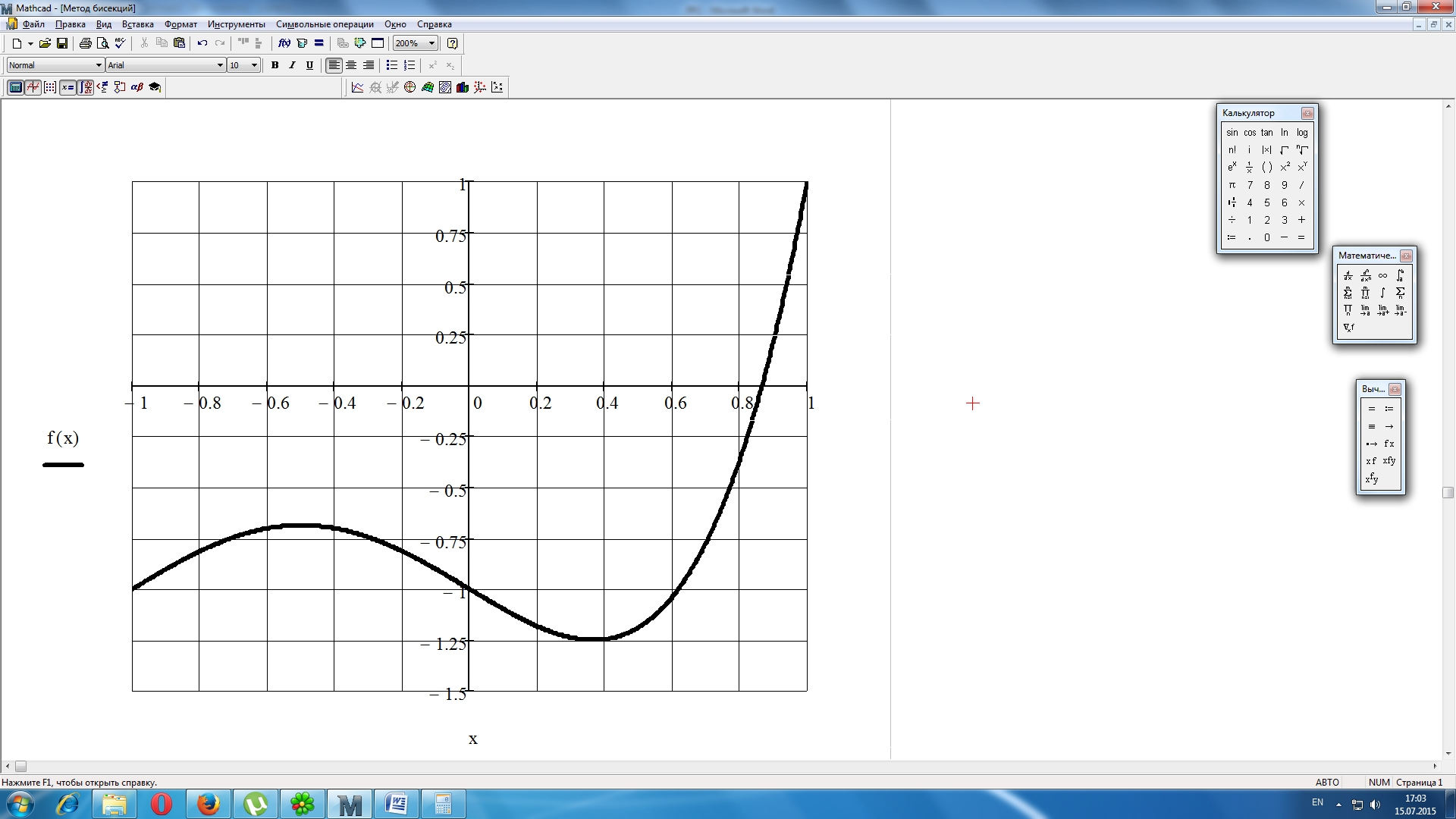
Рисунок 3 Зависимость

Последовательно имеем:

x₀ =0; f(0) = - 1;

x₁=1; f(1) = 1;

f(0,5) = - 1,19;

f(0,75) = - 0,59;

f(0,875) = + 0,05;

Таблица 1.1

Шаг	х	f(x)	Ошибка ɛ
1	0	-1
2	1	1	1
3	0,5	-1.19	0,5
4	0,75	- 0,59	0,25
5	0,875	0,05	0,125
6	0,8125	- 0,304	0,0625
7	0,8438	- 0,135	0,0313
8	0,8594	- 0,043	0,0156
9	0,8672	- 0,649	0,0078
10	0,8711	-0.634	0,0039
11	0,87305	-0.626	0,00195
12	0,874025	-0.622	0,0009 < 0,001

x = 0,874025

Задание к лабораторной работе №1

Таблица 1.1 – Исходные данные для выполнения самостоятельного задания

№ варианта	Функция	Интервал
1		-
2		[-1,0]
3		-
4		[0,3]
5		[1,5]
6		[0,3]
7		[0,3]
8		[1,5]
9		[0,3]
10		[-1,1]
11		[5,10]
12		[0,1]
13		[0,1]
14		[0,1]
15		[0,10]
16		[0,1]
17		[0,5]
18		[0,20]
19		[0.5,2]
20		[0.5,2]

---

Вариант выполнения работы соответствует порядковому номеру в журнале проведения занятий преподавателя. Данные выбираются из табл.1.

1. Построить в среде Mathcad зависимость f(x) и локализовать корни.

2. Рассчитать корни нелинейного уравнения вышеприведенными методами с точностью . Результаты расчетов занести в таблицу результатов расчета;

_{Таблица результатов расчета}

Шаг	х	f(x)	Ошибка ɛ
1
2
N

3. Проверить результаты расчетов в среде Mathcad. Программы расчетов приведены в приложении к методическим указаниям.

Содержание отчета

Отчет по лабораторной работе должен содержать:

1. Титульный лист, оформленный согласно приложению 1;

2. Условие задания и порядок выполнения расчетов.

3. Протокол работы в виде документа Mathcad с текстовыми блоками заголовков заданий и формульных блоков их выполнения по каждому пункту заданию согласно своему варианту;

4. Выводы о проделанной работе.

Приложение Б (рекомендуемое)

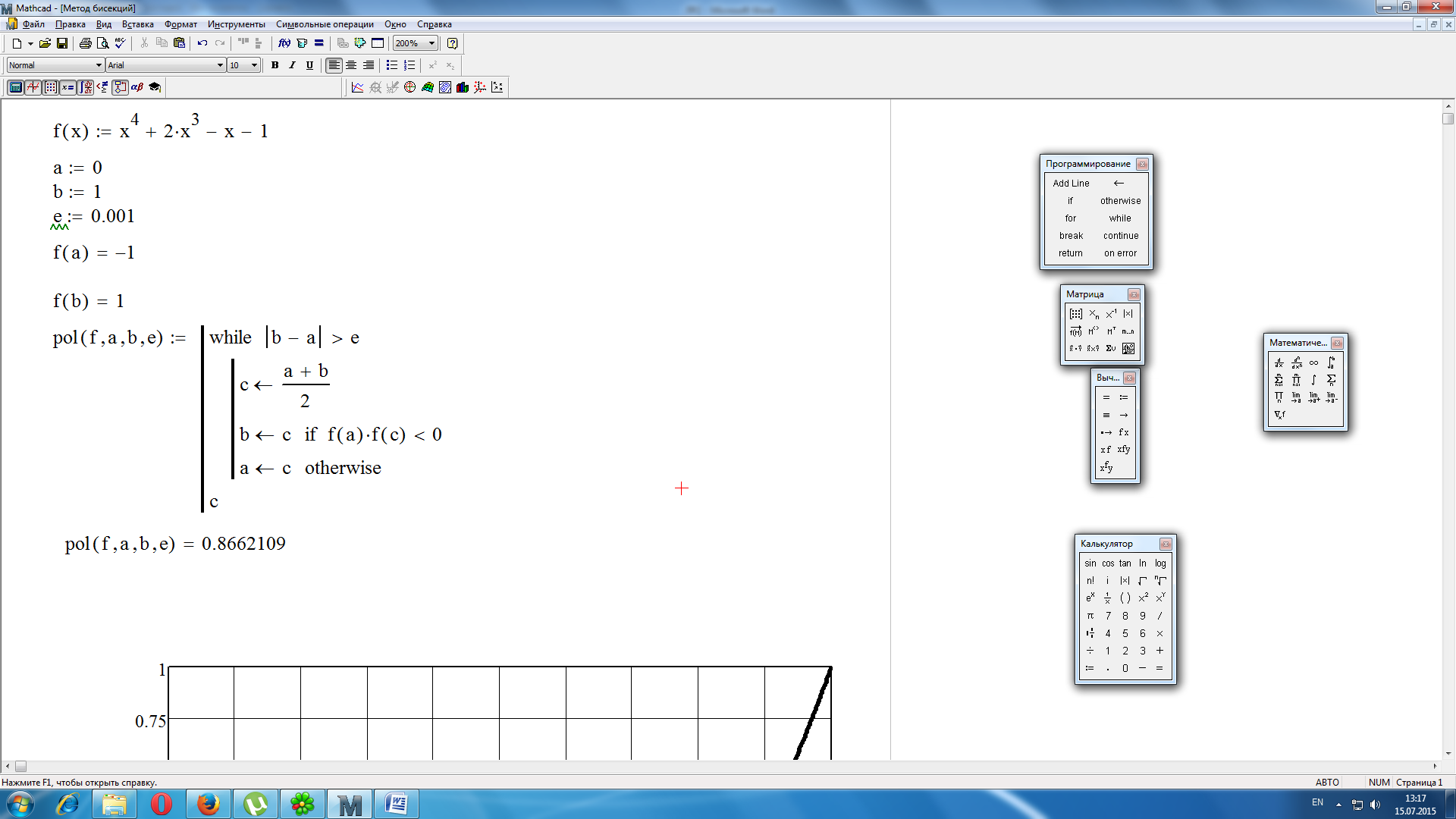
Листинг программы нахождения корня

методом деления отрезка пополам

пределы нахождения корня а =0, b=1

ошибка e =0.001

---

Смотрите также файлы

• Метоодические указания к ЛР.docx

• Реферат учет электроэнергии.docx

• титульник на реферат.docx

• Электрическое освещение зданий.docx

• Электродвигатели и их коммутационные аппараты(Караджаев) — копия.docx