Добавлен: 23.10.2018
Просмотров: 316
Скачиваний: 4
Лабораторная работа № 3
Тема: Рекурсивные функции
Цель работы: Изучить и освоить методы и средства построения примитивно рекурсивных и частично рекурсивных функций, а также получить умения в доказательстве рекурсивности функций.
Требования к выполнению работы
-
Представить заданную функцию через элементарные арифметические функции с использованием трех основных операций.
-
Привести примитивно рекурсивное (частично рекурсивное) описание заданной функции.
-
Выполнить вычисления при x=7, y=4, z=3.
Варианты заданий
Группа а
-

-
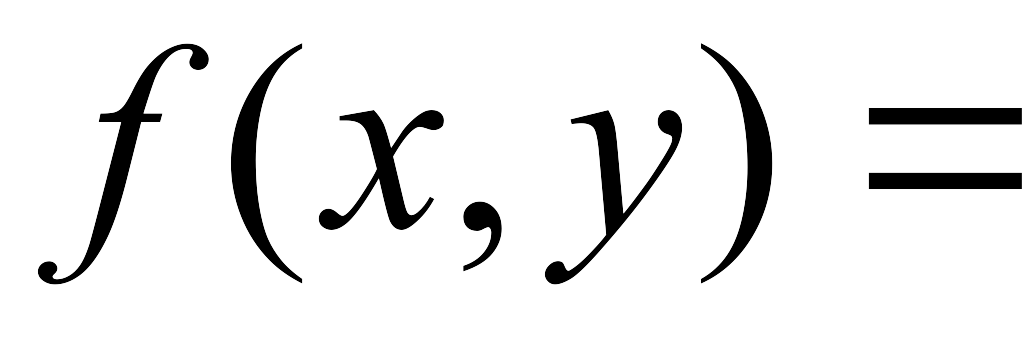 (y3-7)x
(y3-7)x -
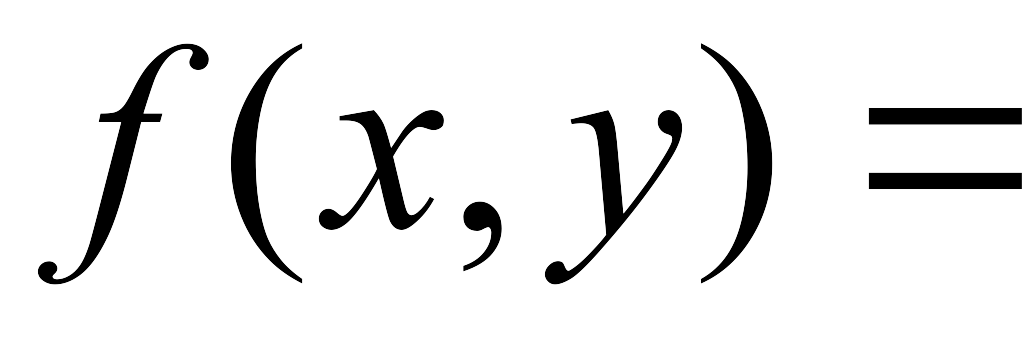 (1+x2)/(y+2)
(1+x2)/(y+2) -
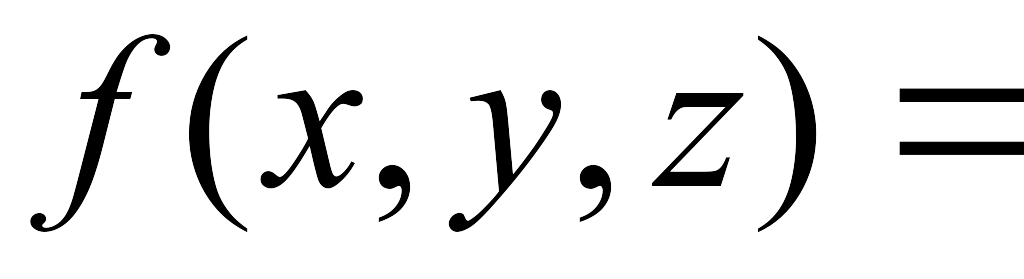 logz((1+x)(z+5))
logz((1+x)(z+5)) -
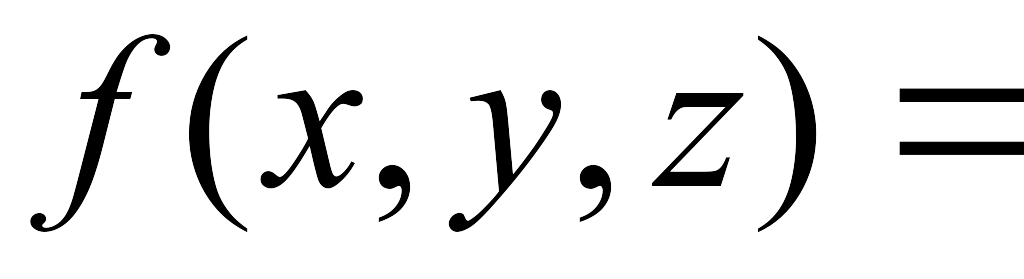 z/(1+x)+4y
z/(1+x)+4y -
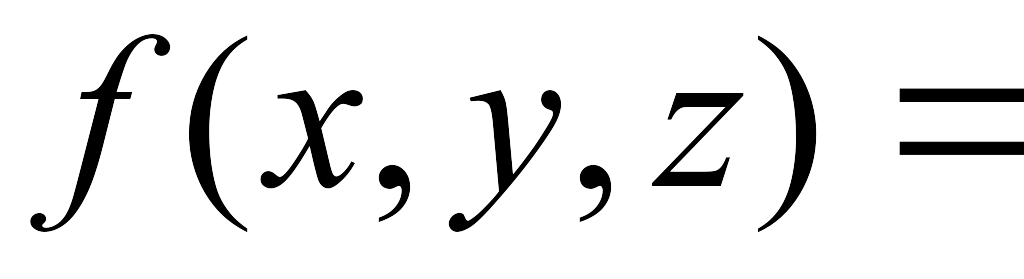 (2x+5y)/(x2-z)
(2x+5y)/(x2-z) -
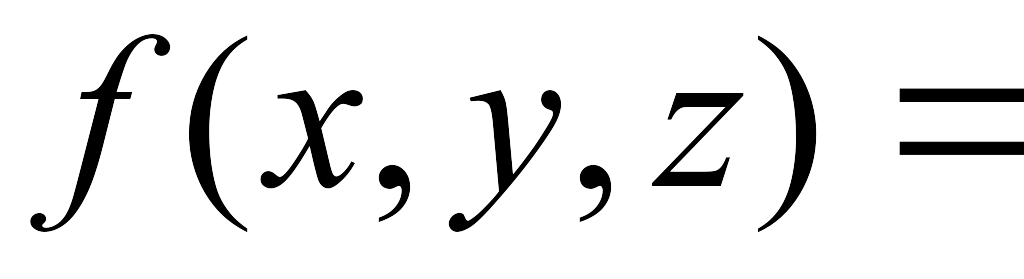
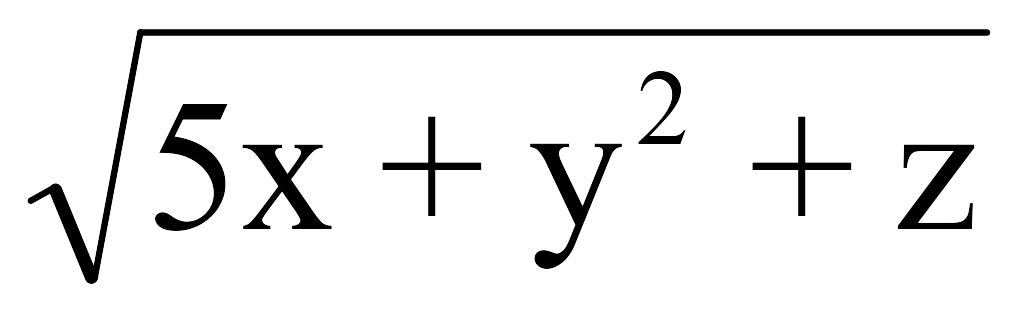
-

-
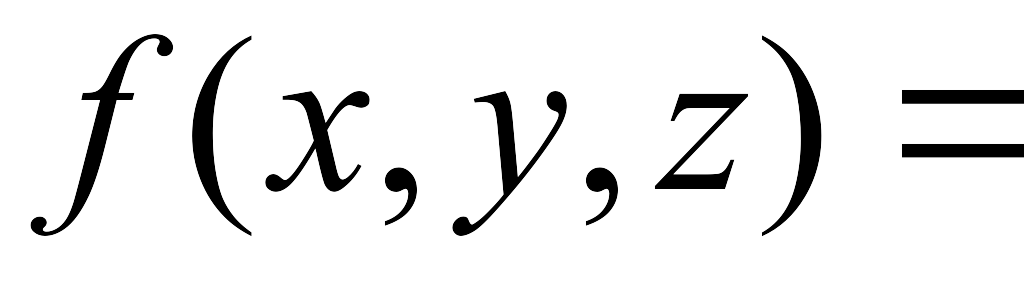 logx(z+1+y2)
logx(z+1+y2) -
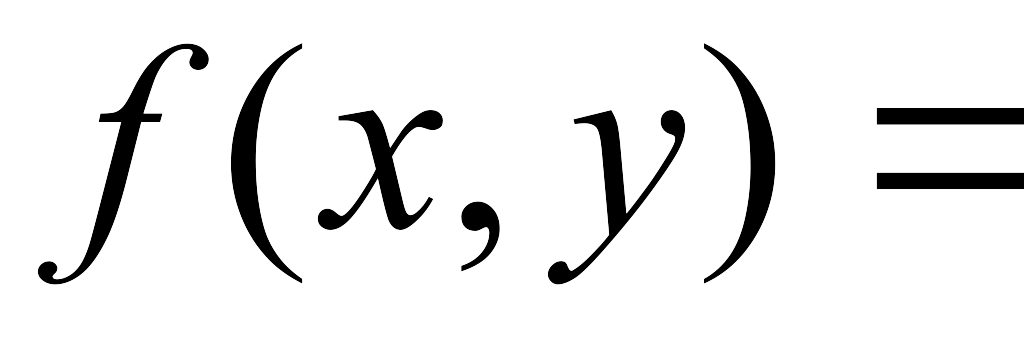
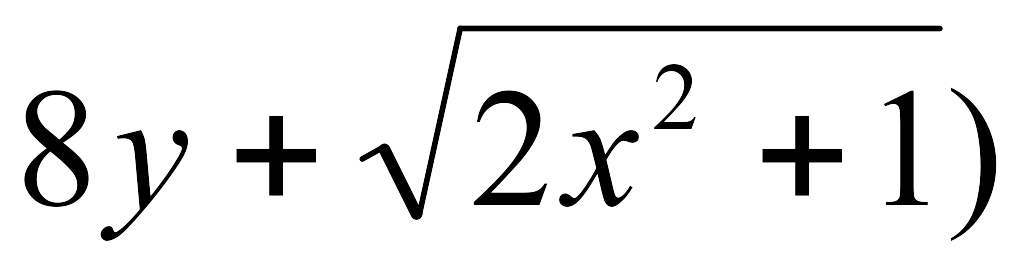
-

-
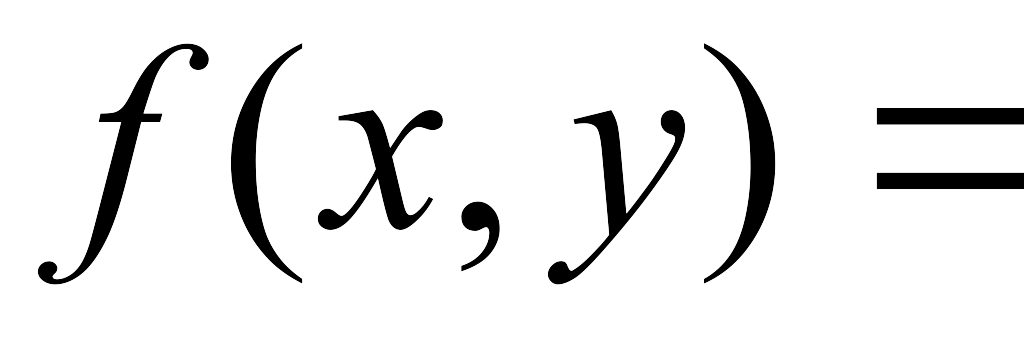 5x-y(6x-3)
5x-y(6x-3) -
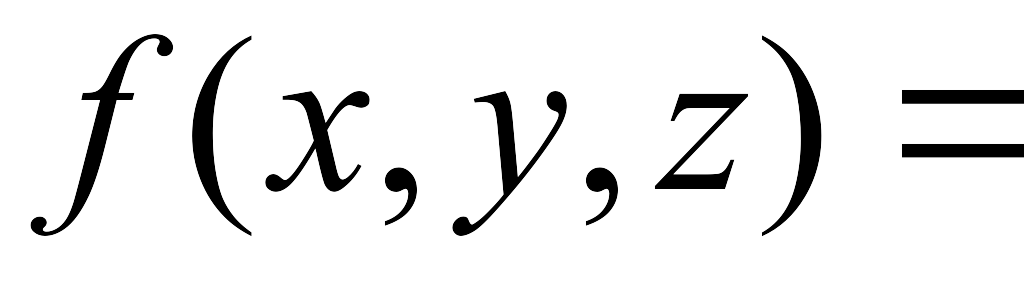 x+y/6)+z(x2-3y+2)
x+y/6)+z(x2-3y+2) -
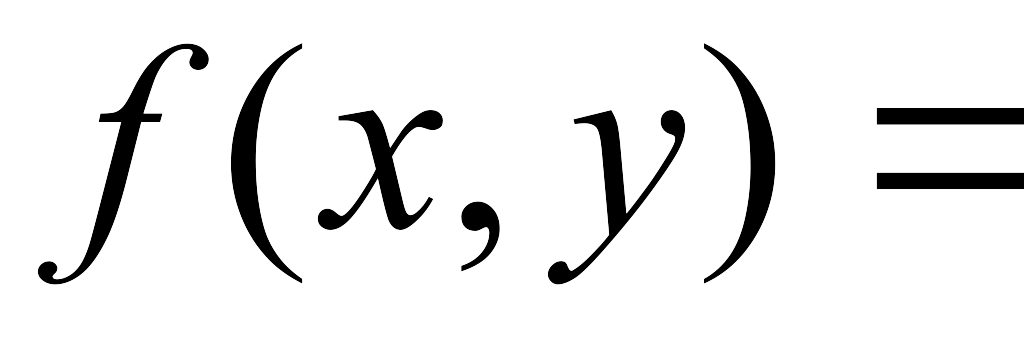 log5(x+1)-y/x2
log5(x+1)-y/x2 -
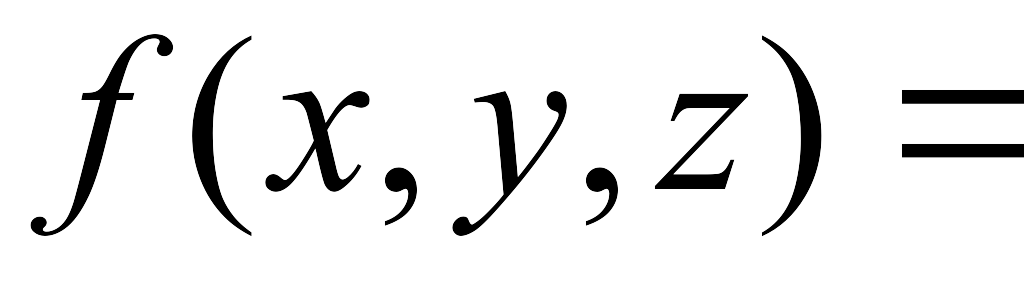 lg(y-1)+z(3x-2)
lg(y-1)+z(3x-2) -
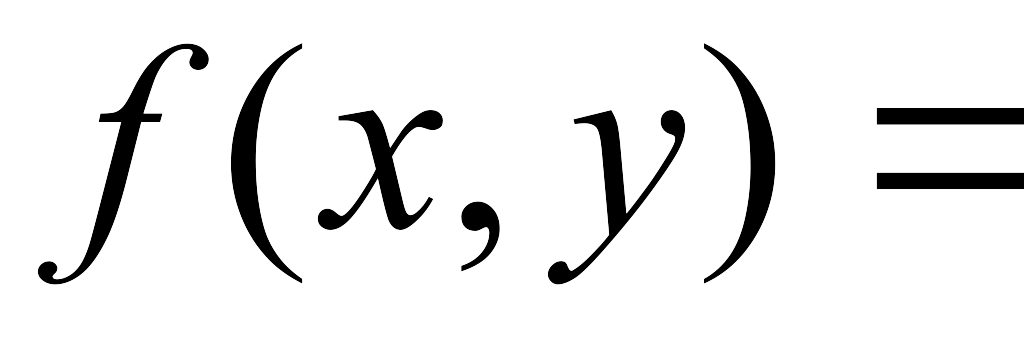 y5x-1
y5x-1 -
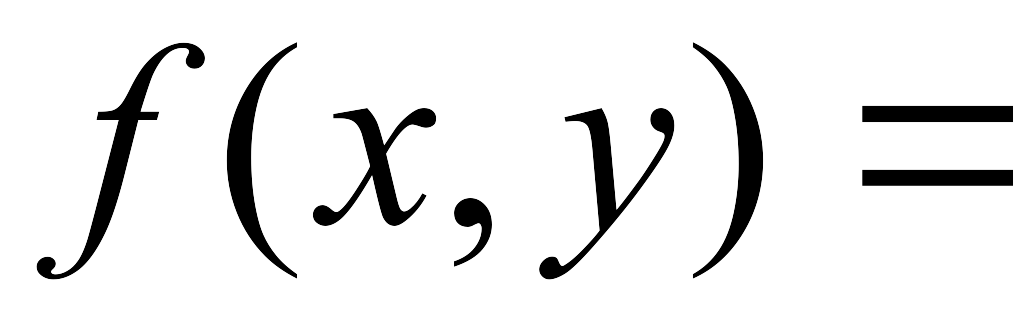 (x(y+1)+2)2
(x(y+1)+2)2 -
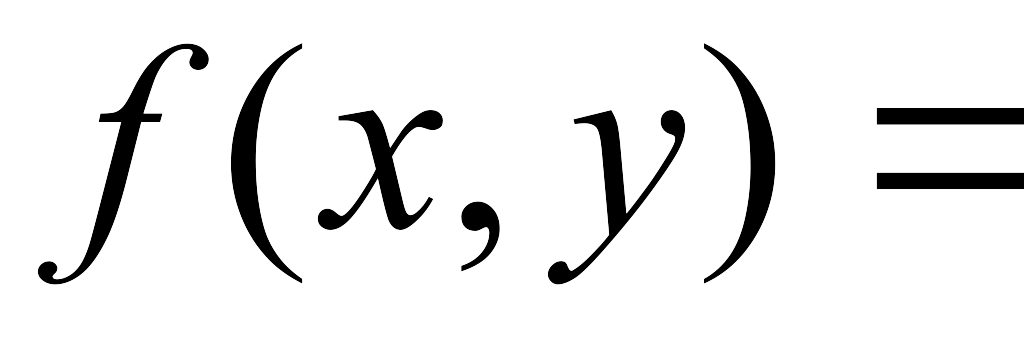 |(x-2)2-1|-y*2-x
|(x-2)2-1|-y*2-x -
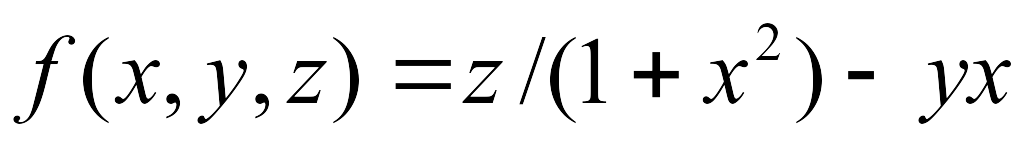
-
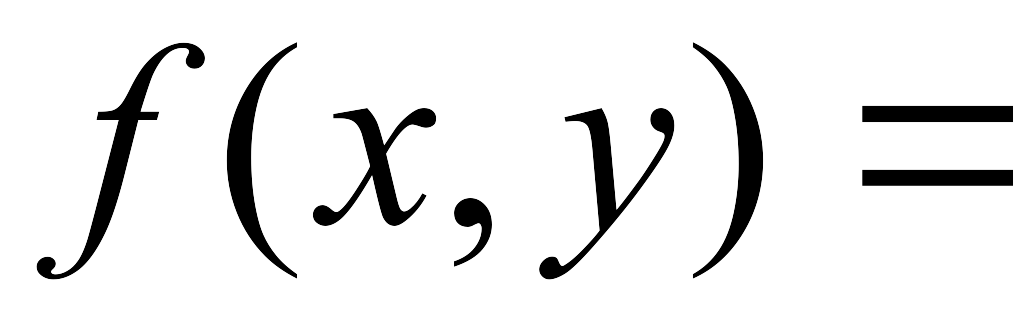 (log3x)2-(yx+4)
(log3x)2-(yx+4)
Группа б
-
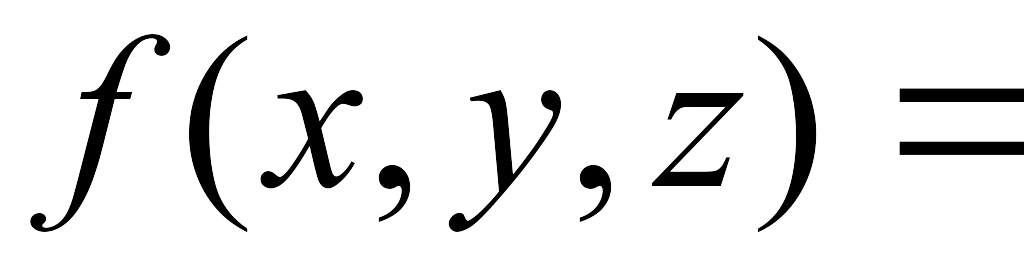 (2x+5y)/(x2-z)
(2x+5y)/(x2-z) -
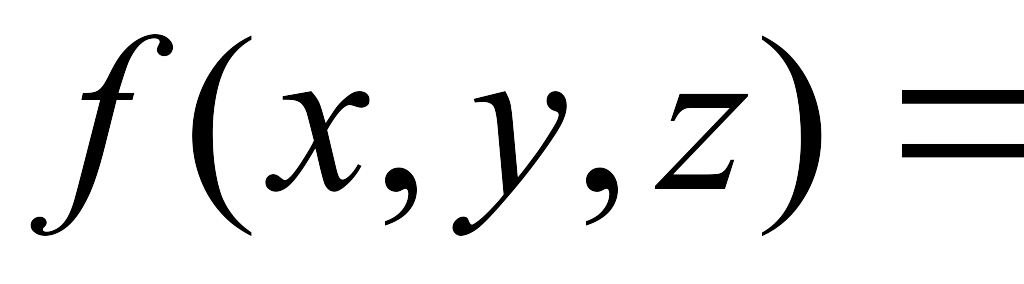 [|17-xy|/z]
– остаток
от целочисленного деления
[|17-xy|/z]
– остаток
от целочисленного деления -
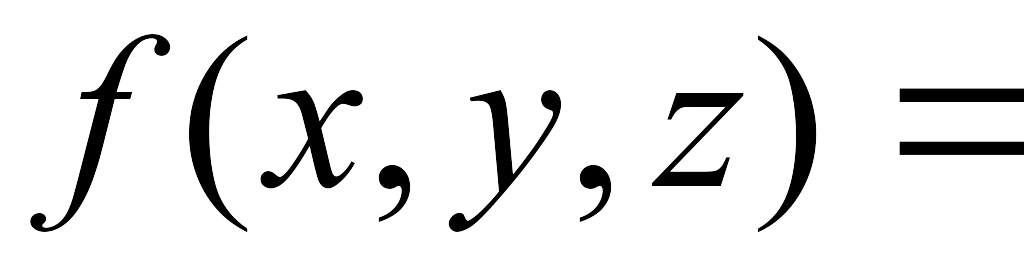 logz((1+x)(z+5))
logz((1+x)(z+5)) -
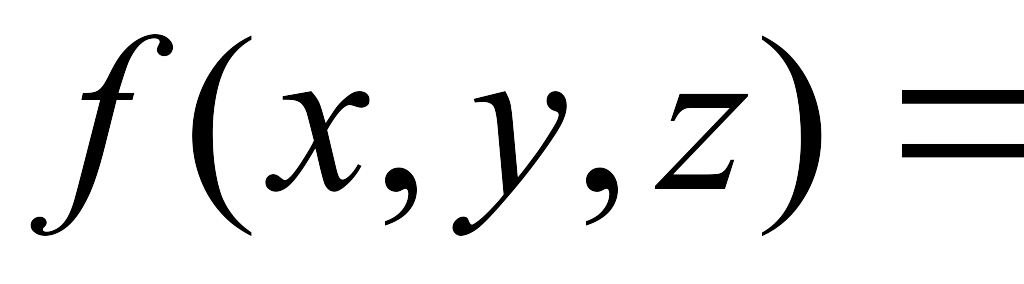 7yx2/(1+z4)
7yx2/(1+z4) -
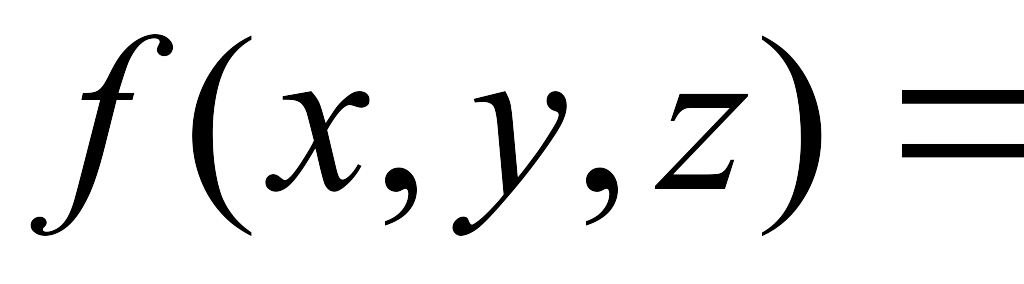 logy(2+x)-yz3
logy(2+x)-yz3 -
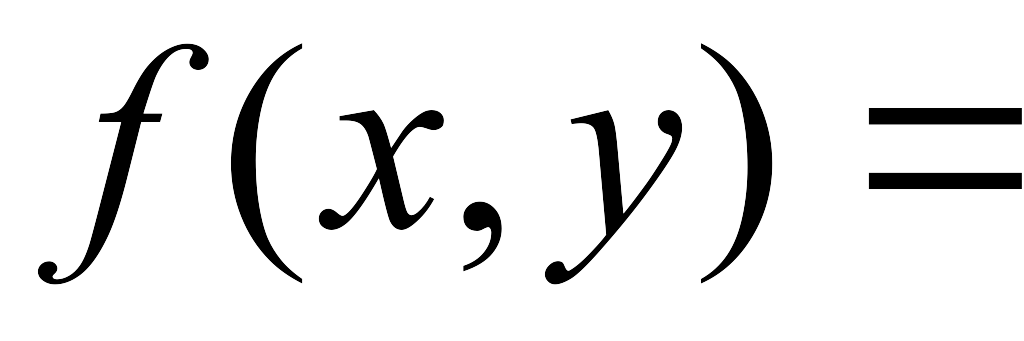 (1+x2)/(y+2)
(1+x2)/(y+2) -
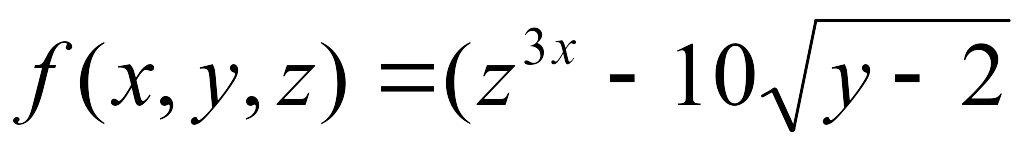
-
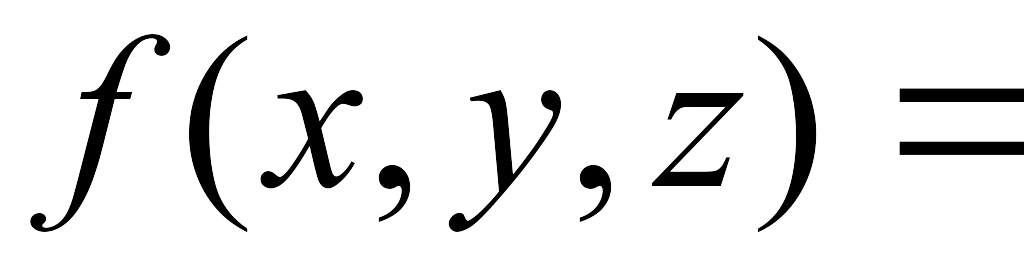 (2x+5y)/(x2-z)
(2x+5y)/(x2-z) -
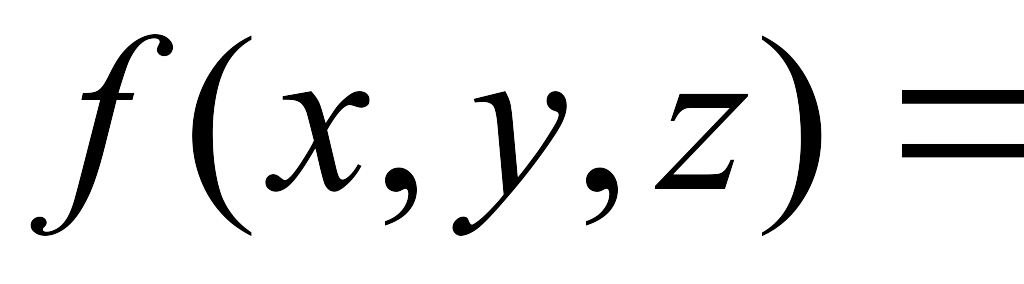 logx(z+1+y2)
logx(z+1+y2) -
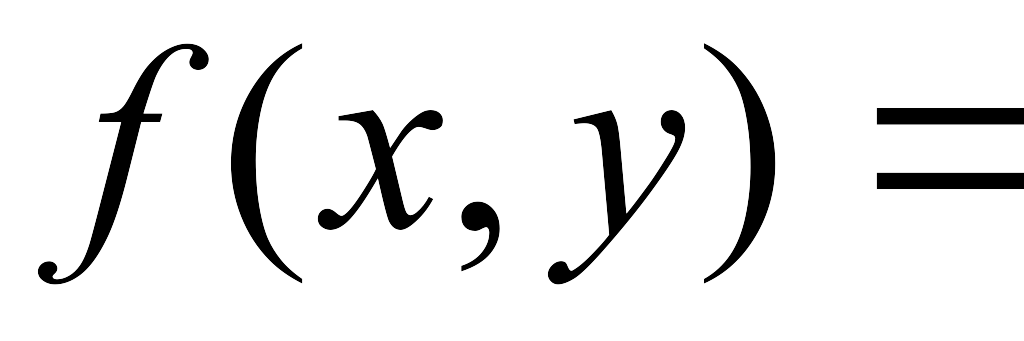 log5(x+1)-y/x2
log5(x+1)-y/x2 -
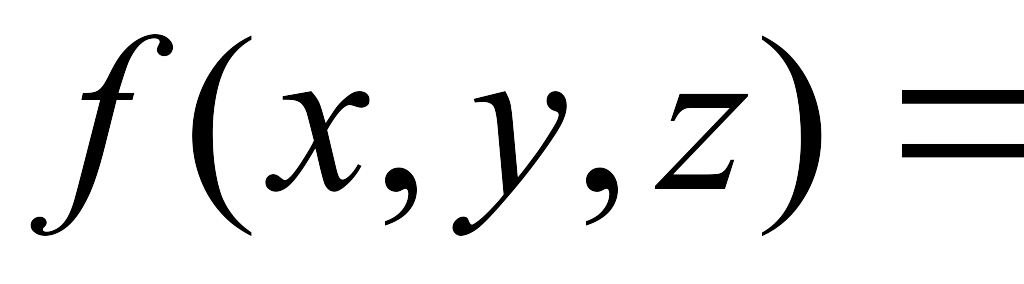 lg(y-1)+z(3x-2)
lg(y-1)+z(3x-2) -
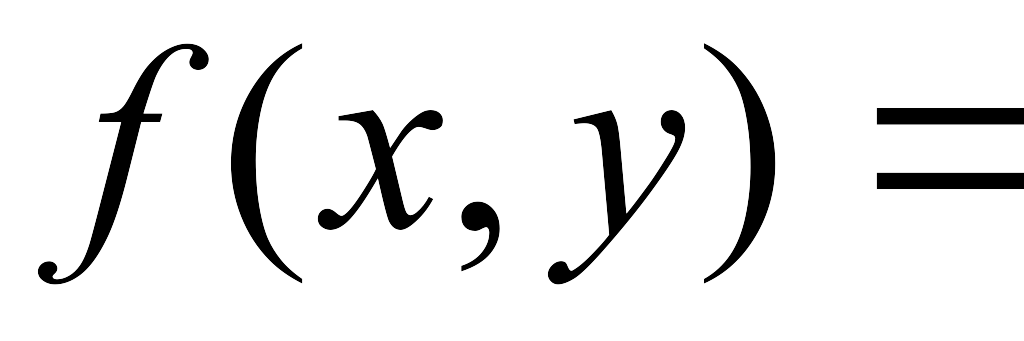
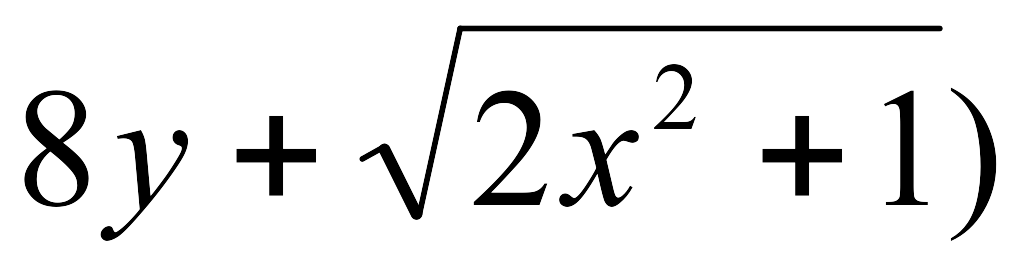
-

-

-
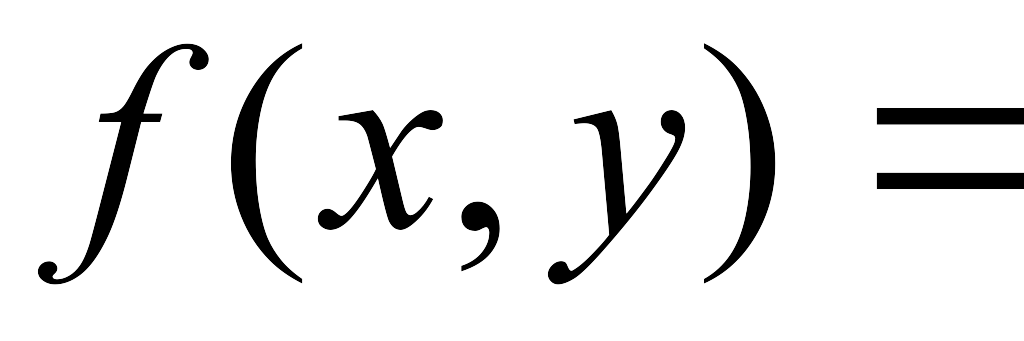 y5x-1
y5x-1 -
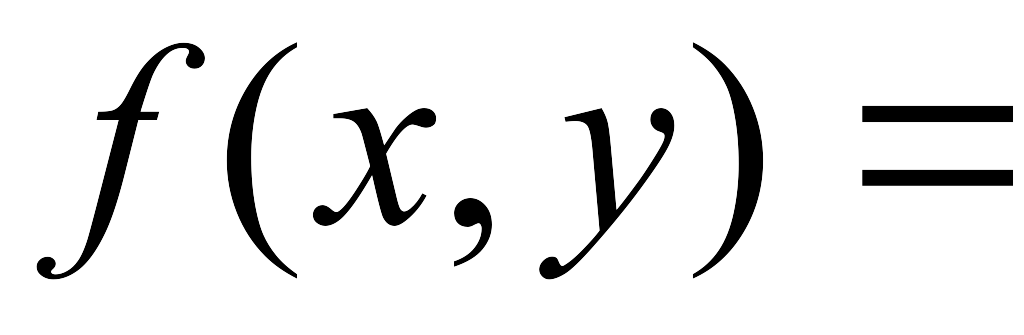 (x(y+1)+2)2
(x(y+1)+2)2 -
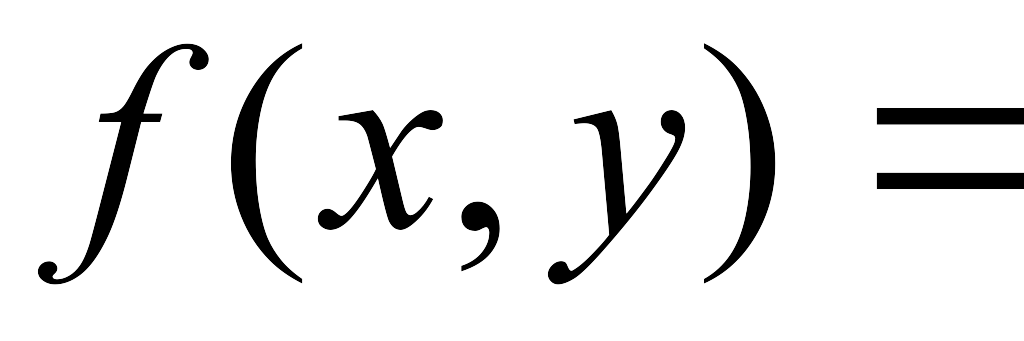 |(x-2)2-1|-y*2-x
|(x-2)2-1|-y*2-x -
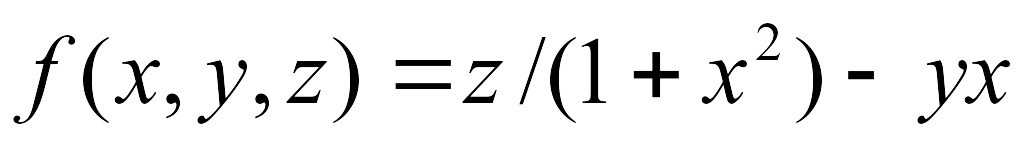
Группа в
-
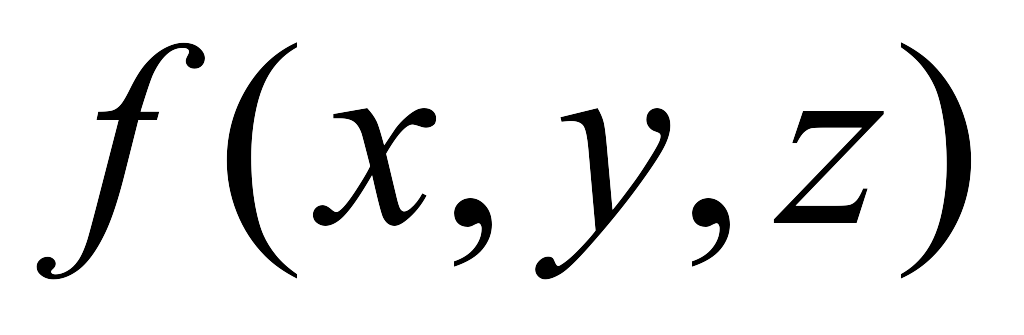 =zx+(y+2)/z
=zx+(y+2)/z -
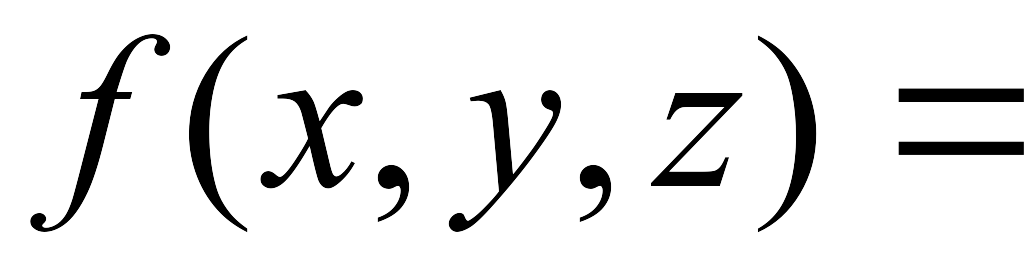 [|17-xy|/z]
– остаток
от целочисленного деления
[|17-xy|/z]
– остаток
от целочисленного деления -
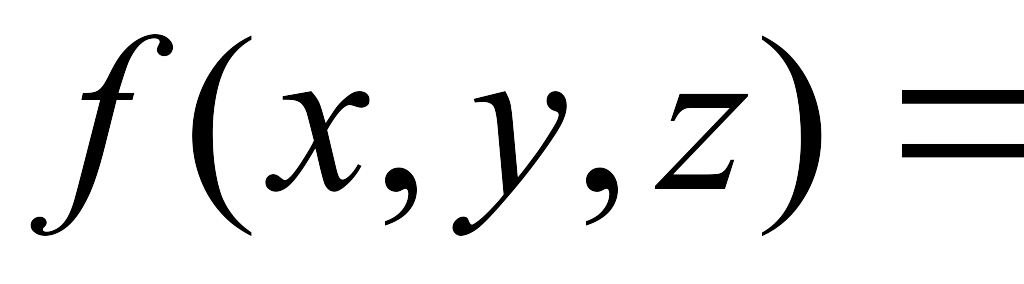 xzlg(y+1)
xzlg(y+1) -
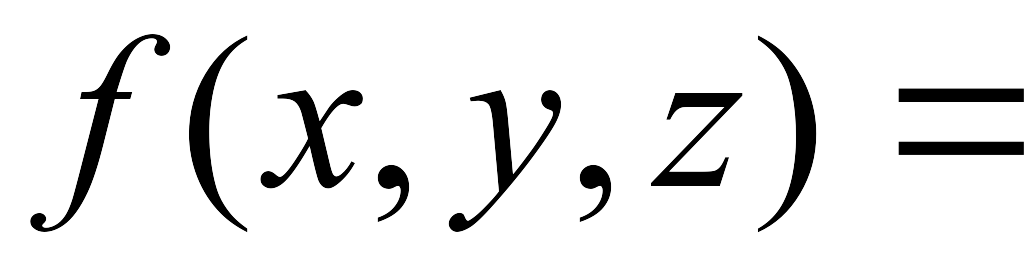 logy(2+x)-yz3
logy(2+x)-yz3 -
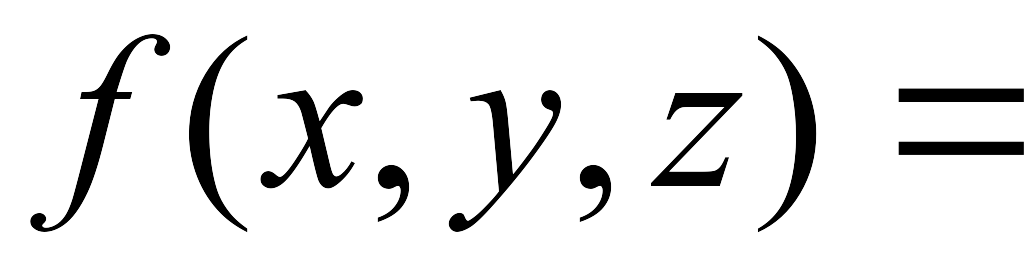 [(3y+2x)/z]
– остаток
от целочисленного деления
[(3y+2x)/z]
– остаток
от целочисленного деления -
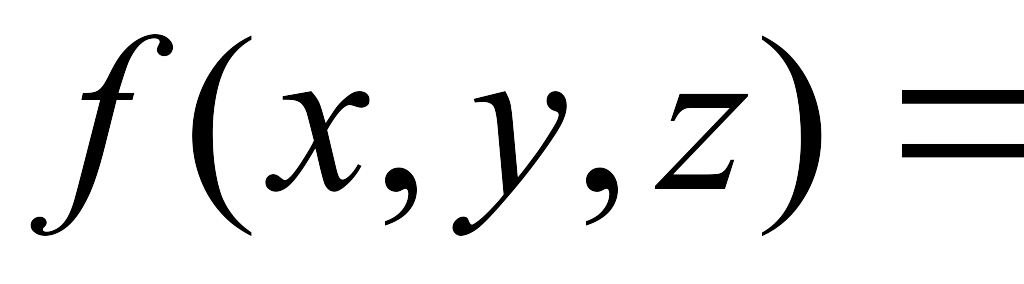 log5(y-xz)
log5(y-xz) -
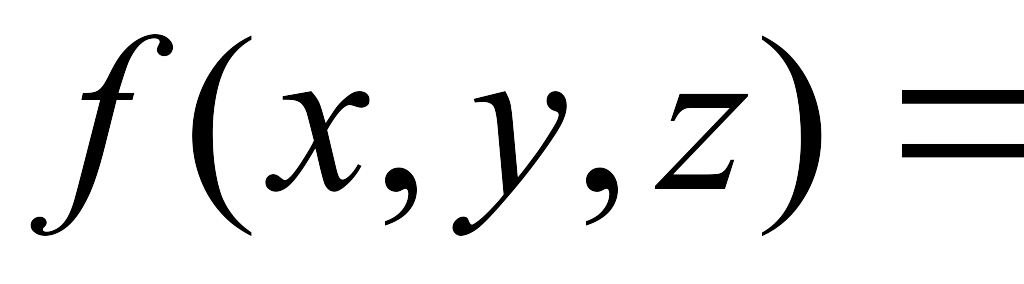
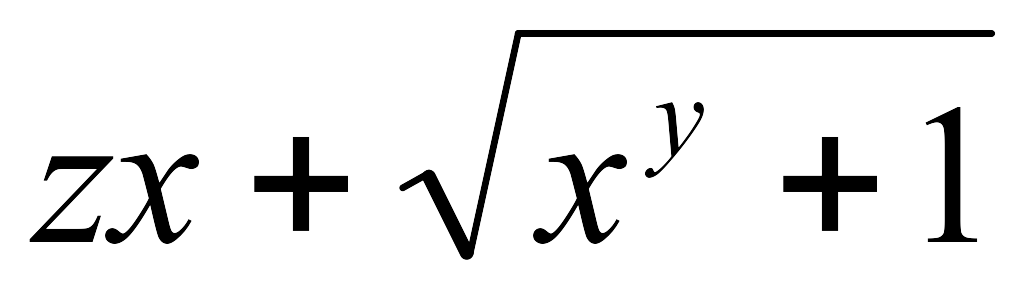
-
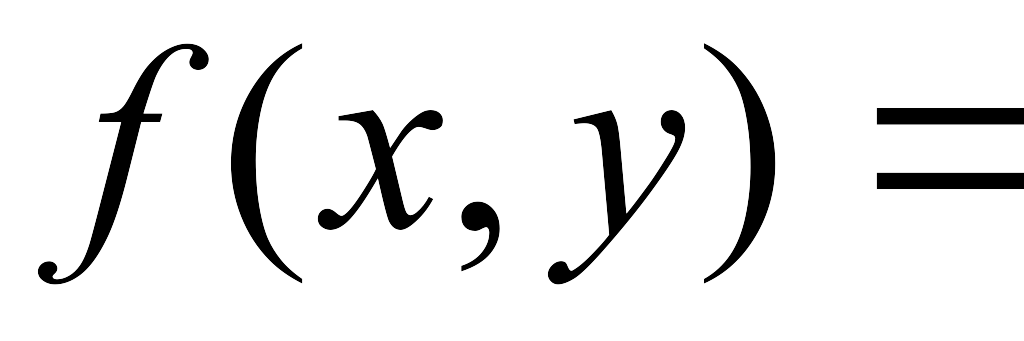 (x3-2y)*102y
(x3-2y)*102y -
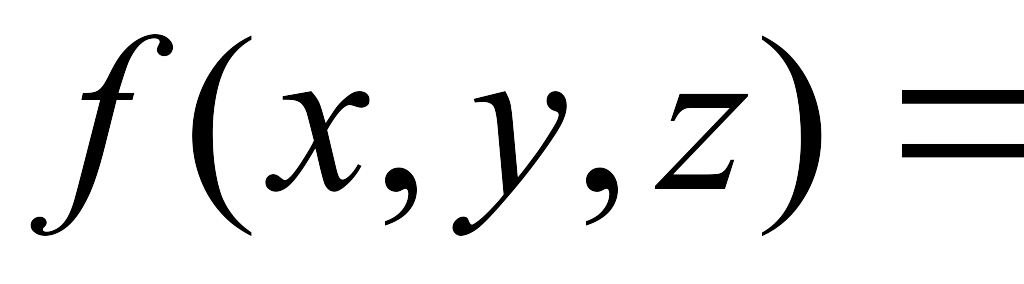

-
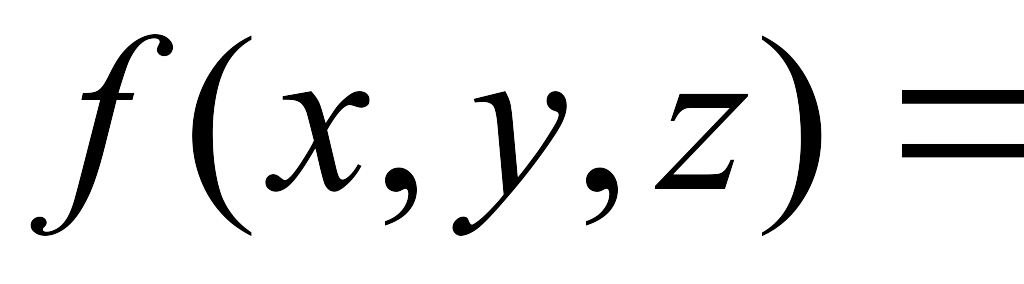 xz+2+7y-3
xz+2+7y-3 -
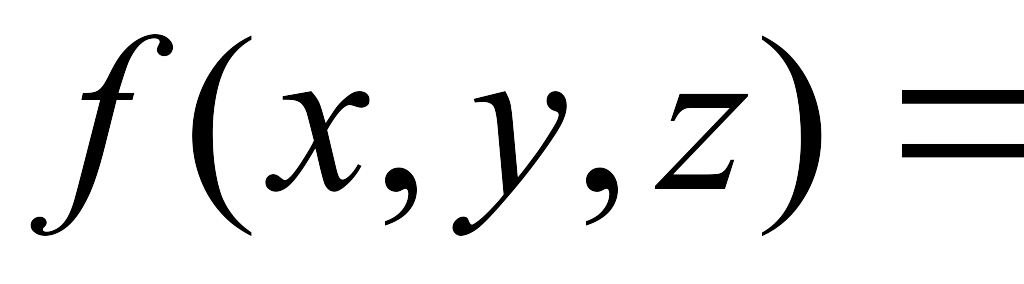 log2(1+x4)*y2
log2(1+x4)*y2 -
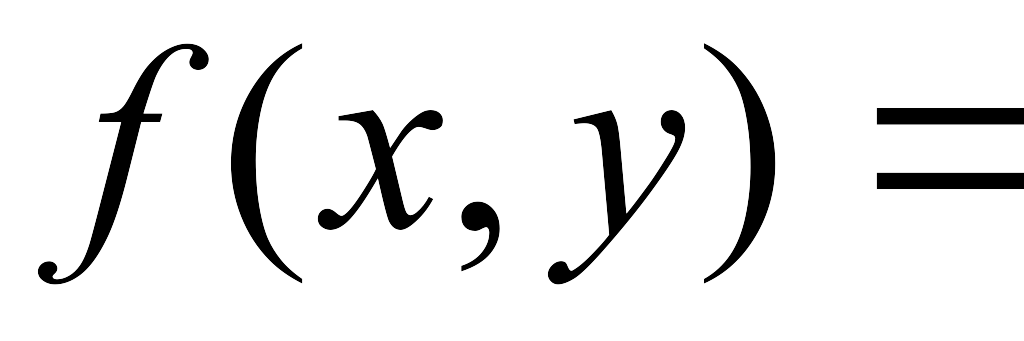 lg(2y+x)+11x3
lg(2y+x)+11x3 -
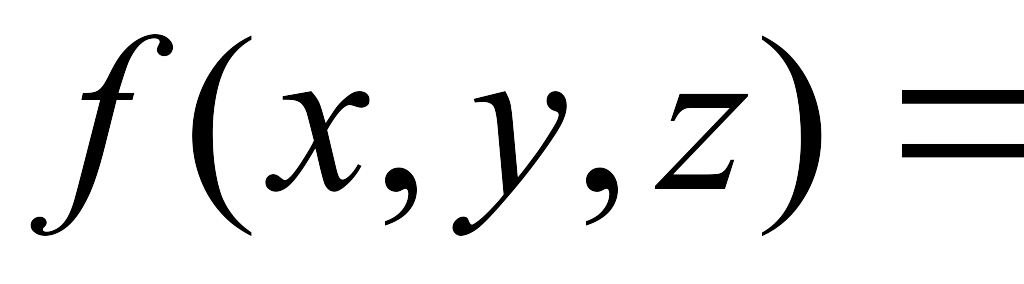 7yx2/(1+z4)
7yx2/(1+z4) -
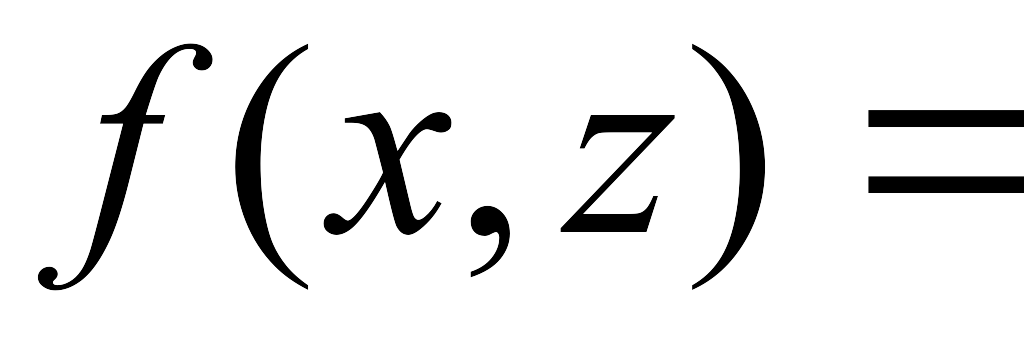
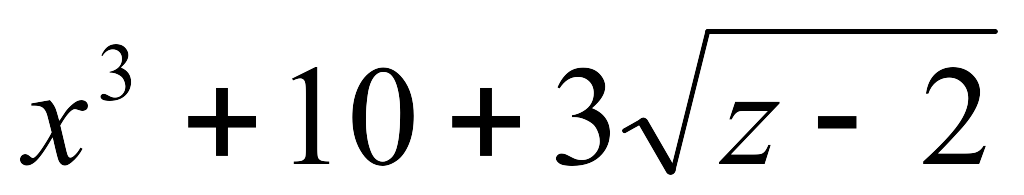
-