Файл: Контрольная теория информационных процессов и систем.pdf
ВУЗ: Поволжский Государственный Университет Телекоммуникаций и Информатики
Категория: Методичка
Дисциплина: Теория систем
Добавлен: 26.10.2018
Просмотров: 1028
Скачиваний: 14
6
19
3
0,1; 0,1; 0,4; 0,4
p(y
2
=0/y
1
=0)
20
3
0,2; 0,2; 0,3; 0,3
p(y
2
=0/y
1
=0)
21
6
0,5; 0,25; 0,125; 0,125
p(y
2
=1/y
1
=0)
22
6
0,1; 0,2; 0,3; 0,4
p(y
2
=1/y
1
=0)
23
6
0,1; 0,1; 0,4; 0,4
p(y
2
=1/y
1
=0)
24
6
0,2; 0,2; 0,3; 0,3
p(y
2
=1/y
1
=0)
25
7
0,5; 0,25; 0,125; 0,125
p(y
2
=1)
26
7
0,1; 0,2; 0,3; 0,4
p(y
2
=1)
27
7
0,1; 0,1; 0,4; 0,4
p(y
2
=1)
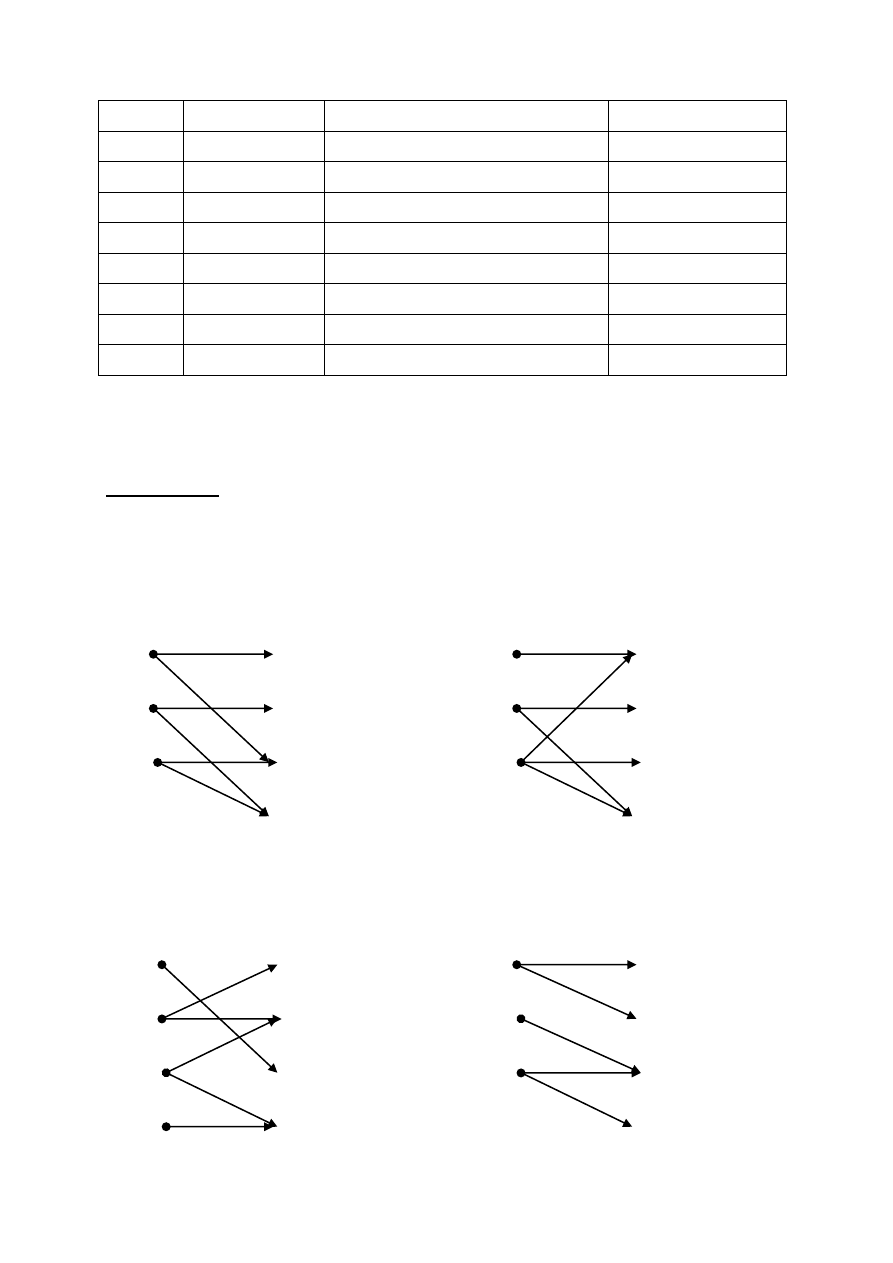
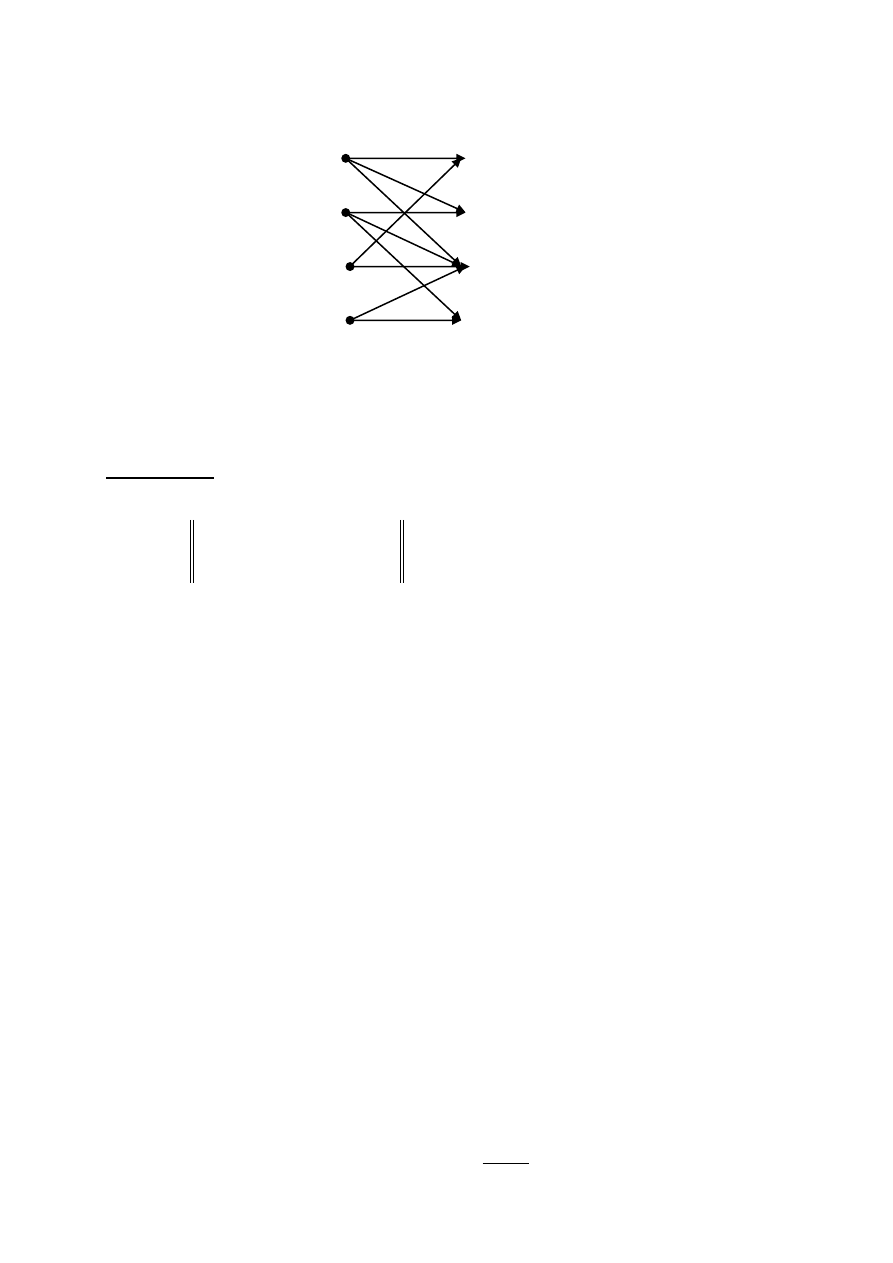
Задача №2. Для заданных: источника (1) и дискретного канала Р , номер
рисунка графа которого задаётся столбцом 2 таблицы 1, определить;
H(X); H(Y); H(Y/X); Y(X/Y); I(X;Y).
Рис. 1
X
Y
X
Рис. 2
Y
Рис. 3
Y
X
Рис. 4
X
Y
7
Задача №3 Сообщения дискретного источника X описываются матрицей
X=
)
x
(
p
),...,
x
(
p
),
x
(
p
x
,...,
x
,
x
N
2
1
N
2
1
,
(2)
Вероятности
)
x
(
p
),...,
x
(
p
),
x
(
p
N
2
1
задаются таблицей 2 (столбец 2) по
номеру варианта.
Закодировать сообщения равномерным двоичным кодом и заданным
эффективным кодом (таблица 2, столбец 3).
Определить:
1)избыточность на входе X и выходе Y кодеров;
2)среднюю длину кодовых слов для указанных способов кодирования и их
границы;
3)сформулировать вывод по результатам расчётов по п.п. 1и 2.
Для выполнения задачи 3 следует изучить материал источника Л1, глава3.
Особое внимание обратить на примеры кодирования по методам Шеннона-
Фано и Хаффмена.
Избыточность источника Х определяется по формуле [1]
,
)
(
1
)
(
gN
X
H
X
R
Рис. 7
X
Y

8
где R(X) – избыточность источника Х;
H(X) – энтропия источника Х;
N – количество сообщений источника Х.
Избыточность эквивалентного источника на выходе кодера рассчитывается
по формуле
,
)
(
1
)
(
gN
n
X
H
X
R
где
n
– средняя длина кодового слова [1].
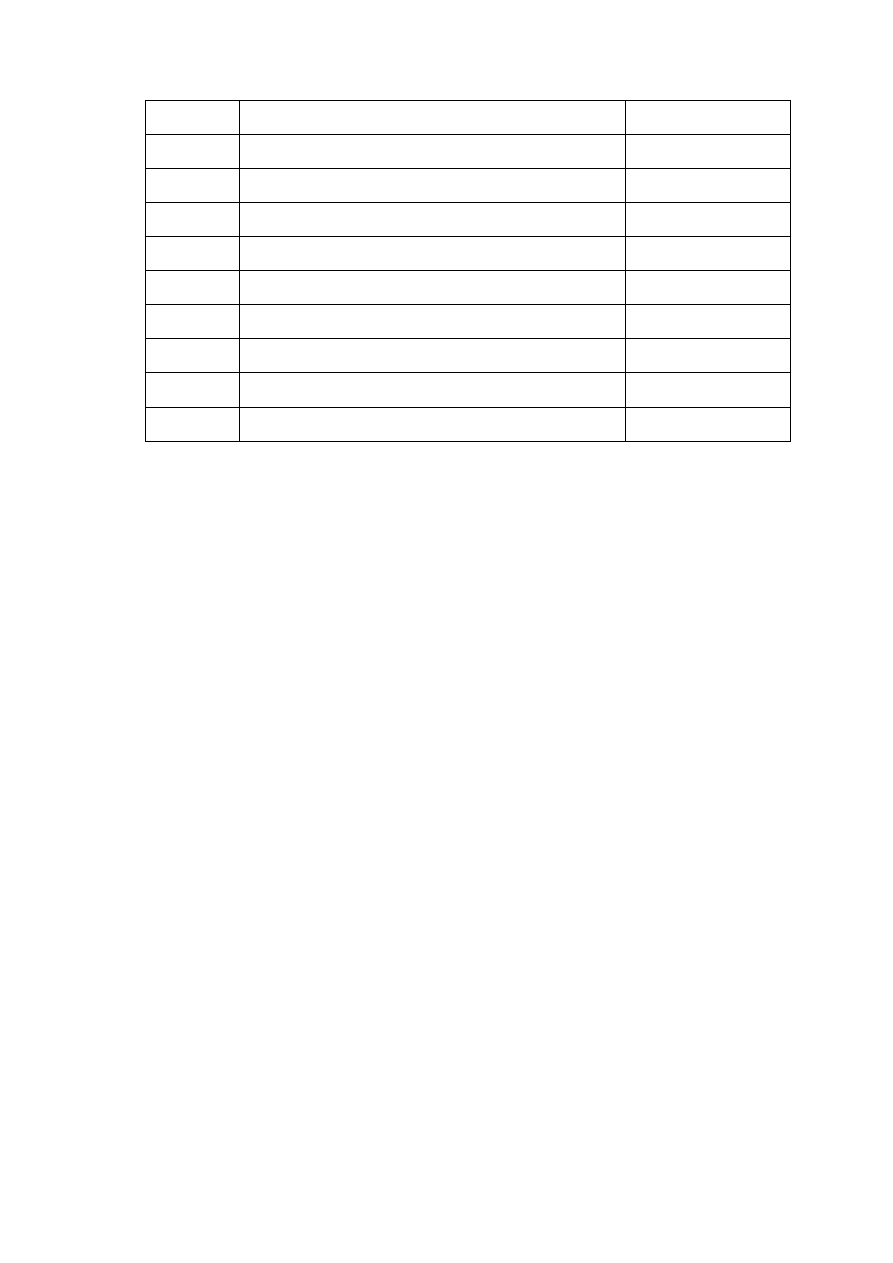
Таблица 2
№
варианта
Вероятности сообщений
)
x
(
p
N
Метод
эффективного
кодирования
1
2
3
1
0,1; 0,1; 0,2; 0,05; 0,05; 0,5
Хаффмен
2
0,1; 0,3; 0,05; 0,05; 0,05; 0,45
Шеннон – Фано
3
0,2; 0,1; 0,1; 0,1; 0,2; 0,3
Хаффмен
4
0,2; 0,3
; 0,05; 0,1; 0,05; 0,3
Шеннон – Фано
5
0,1; 0,2; 0.1; 0.1; 0.2; 0.3
Хаффмен
6
0,2; 0,2; 0,1; 0,1; 0,1; 0,3
Шеннон – Фано
7
0,3; 0,1; 0,2; 0,1; 0,2; 0,1
Хаффмен
8
0,3; 0,05; 0,1; 0,1; 0,3; 0,15
Шеннон – Фано
9
0,3; 0,2; 0,1; 0,1; 0,25; 0,05
Хаффмен
10
0,15; 0,25; 0,2; 0,1; 0,2; 0,1
Шеннон – Фано
11
0,1; 0,2; 0,1; 0,05; 0,05; 0,1; 0,4
Хаффмен
12
0,1; 0,25; 0,15; 0,05; 0,05; 0,2; 0,2
Шеннон – Фано
13
0,1; 0,3; 0,05; 0,05; 0,1; 0,2; 0,2
Хаффмен
14
0,2; 0,1; 0,1; 0,05; 0,05; 0,3; 0,2
Шеннон – Фано
15
0,2; 0,3; 0,1; 0,1; 0,1; 0,1; 0,1
Хаффмен
16
0,3; 0,1; 0,1; 0,15; 0,15; 0,1; 0,1
Шеннон – Фано
17
0,15; 0,25; 0,1; 0,05; 0,05; 0,1; 0,3
Хаффмен
9
18
0,1; 0,05; 0,15; 0,05; 0,1; 0,1; 0,05; 0,4
Шеннон – Фано
19
0,2; 0,05; 0,15; 0,05; 0,05; 0,2; 0,1; 0,2
Хаффмен
20
0,1; 0,15; 0,15; 0,05; 0 05; 0,1; 0,3; 0,1
Шеннон – Фано
21
0,1; 0,2; 0 05; 0,05; 0,1; 0,2; 0,2; 0,1
Хаффмен
22
0,2; 0,1; 0,1; 0,15; 0,15; 0,05; 0,05; 0,2
Шеннон – Фано
23
0,2; 0,05; 0,05; 0,1; 0,1; 0,15; 0,15; 0,2
Хаффмен
24
0,3; 0,1; 0,1; 0,05; 0,05; 0,15; 0,15; 0,1
Шеннон – Фано
25
0,3; 0,05; 0,05; 0,1; 0,15; 0,15; 0,1; 0,1
Хаффмен
26
0,2; 0,1; 0,1; 0,05; 0,05; 0,2; 0,15; 0,15
Шеннон – Фано
27
0,05; 0,2; 0,15; 0,15; 0,2; 0,1; 0,05; 0,1
Хаффмен