ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Системы искусственного интеллекта
Добавлен: 29.10.2018
Просмотров: 893
Скачиваний: 12
Лекция 4. Стратегии поиска.
4.1. Оценки успеха при поиске цели.
Оценки успеха, характеризующие эффективность поиска, могут быть самыми различными. Будем полагать, что оценка успеха является положительным числом или нулем и чем больше число, тем успешнее действует агент. Тогда самая очевидная оценка — это возможность достижения цели вообще. Эта оценка носит двузначный характер: например, она принимает некоторое максимальное значение, если цель достижима, и минимальное в противном случае.
Другая оценка может быть ценой пути, вычисляемой с помощью функции цены пути.
Третья оценка может быть ценой поиска, характеризующейся объемом необходимых для поиска времени и памяти. Наконец, еще одна оценка успеха может быть общей ценой, являющейся некоторой функцией от цены пути и цены поиска.
Цена поиска зависит от многих обстоятельств. Так, например, если агент сильно стеснен во времени, то цена поиска может быть пропорциональна времени, затрачиваемому на поиск. Общая цена может зависеть от пройденного расстояния и затраченного на поиск времени. Вычисление общей цены непростая задача, поскольку выбор пути, а следовательно, и пройденное расстояние могут определяться временем, затраченным на поиск. Чем меньше времени потрачено на поиск, тем дальше от оптимального может оказаться выбор пути. Зачастую в этих условиях приходится идти на некий компромисс, далекий от оптимального решения.
Стратегии поиска различаются последовательностью или порядком просмотра состояний или множеств состояний в пространстве всех состояний среды. Стратегии поиска в пространстве состояний обычно сравнивают по ряду критериев. Основными критериями являются следующие.
Полнота: стратегия является полной при условии, что она всегда обеспечивает нахождение решения (целевого состояния или состояний), если оно вообще существует в данном пространстве состояний.
Сложность по времени: время, необходимое для нахождения решения.
Сложность по памяти: объем памяти, необходимый для решения задачи.
Оптимальность: стратегию называют оптимальной при условии, что она обеспечивает нахождение решения, которое может не быть наилучшим, но известно, что оно принадлежит некоторому классу или подмножеству, все элементы которого обладают неким общим свойством (или свойствами), согласно которому мы их относим к оптимальным решениям.
Минимальность: стратегия является минимальной, если она гарантирует нахождение наилучшего решения. Минимальность, таким образом, является частным и более сильным случаем оптимальности.
Стратегии поиска разбивают на две большие группы: слепой поиск и направленный поиск. Различие между слепым и направленным поиском можно продемонстрировать на следующем простом примере. Представим себе, что агент приехал в Россию по туристической путевке с целью совершить путешествие по золотому кольцу России. Его самолет сел в аэропорту Шереметьево.
Обратный вылет тоже из Шереметьева. Путешествие по золотому кольцу агент совершал на автобусе. Посетив все города золотого кольца, агент самостоятельно поехал в близлежащий город Иваново, где задержался и отстал от автобуса. В отличие, например, от Ярославля, Иваново не имеет прямой автострады, соединяющей его с Москвой. У агента есть обратный билет на самолет с датой вылета на следующий день, билет не может быть продлен, да к тому же обратных билетов вообще нет на ближайшие две недели. Срок визы также заканчивается через два дня. Отправляясь в поездку, агент ставил перед собой, помимо туристических, несколько других целей: улучшить знание русского языка, завязать полезные деловые контакты, написать несколько пейзажей с видами русской природы и т.п. Но, учитывая серьезность ситуации, главной его целью теперь стало вовремя добраться до аэропорта Шереметьево, не опоздав на свой самолет. После формулировки главной цели агент может принимать во внимание и другие факторы, влияющие на ее достижение.
Прежде всего, следует решить, что мы будем понимать под действиями и состояниями. Если бы вдруг нам пришло в голову в качестве действий выбрать такие, как «повернуть руль на 10 градусов» или «продвинуться вперед на 1 метр», то решение задачи на таком уровне детализации стало бы практически неразрешимой задачей. В нашем случае в качестве действий лучше всего выбрать переезд из одного города в другой, а в качестве состояний нахождение агента в том или ином населенном пункте. Целевым состоянием в этом случае будет нахождение агента в аэропорту Шереметьево (в Москве).
Поиск будет слепым, если агент не имеет никакой информации о дорогах, ведущих из Иванова в другие города, и будет перебирать все дороги подряд. И наоборот, его поиск станет направленным, если он ознакомится с картой, увидит, что Москва лежит на юго-западе от Иванова, и будет пытаться выбирать дороги, ведущие в юго-восточном или близком к нему направлении.
4. 2. Слепой поиск
4.2.1. Поиск в ширину
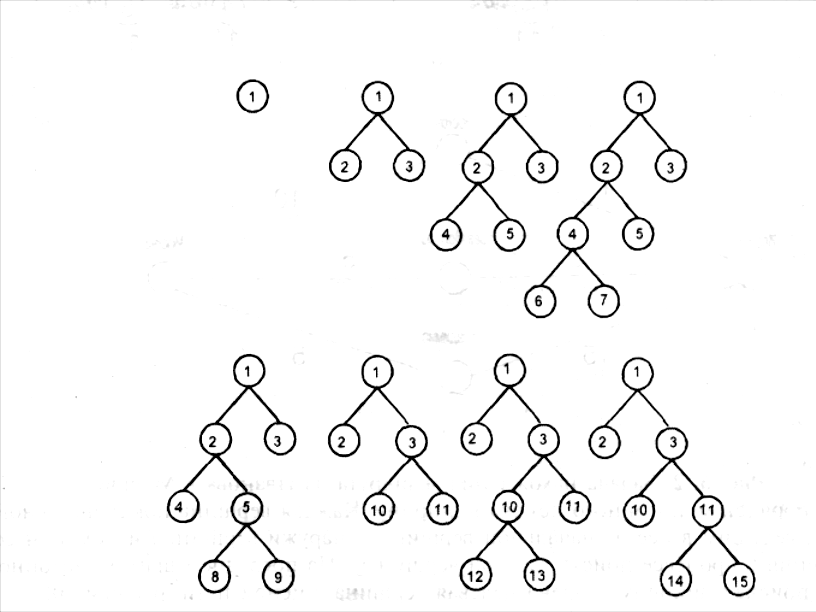
Одна из самых очевидных стратегий поиска называется поиском в ширину. Поиск начинается с корневой вершины, определяются все последователи корневой вершины, затем все последователи каждого из последователей корневой вершины, далее все последователи каждого из последователей, найденных на предыдущем шаге, и т.д. до тех пор, пока не будут найдены все вершины, соответствующие целевым состояниям. Согласно этой стратегии, вершины глубиной k ищутся после того, как будут найдены все вершины глубиной k-1. На рис. 4. 1 показана последовательность нахождения вершин при поиске в ширину и при числе последователей каждой вершины, равном 2.
При поиске в ширину сначала рассматриваются все пути, длина которых равна 1, затем длиной 2 и т.д. Очевидно, что поиск в ширину удовлетворяет критерию полноты и минимальности, поскольку в процессе этого поиска рассматриваются все пути, ведущие из начальной вершины (состояния) во все остальные.
Оценим время и память, затрачиваемые в процессе поиска в ширину. Будем полагать, что число последователей каждой вершины равно l. Тогда в начале поиска в ширину мы имеем одну начальную вершину, затем l последователей, потом l2 последователей и т.д. В общем случае при глубине дерева поиска, равной к, число вершин, изучаемых в процессе поиска, равно 1 + l+ l 2+ l 3+ ...+ l k. При конкретных значениях l и k по этой формуле можно вычислить максимальное число вершин дерева поиска, которое может быть получено в процессе поиска в ширину. Естественно, решение можно найти раньше, чем будут найдены все последователи.
Однако для некоторых задач эта величина может быть достигнута. Обычно вместо этой формулы употребляют ее обозначение в виде O(l k), которое называют экспоненциальной оценкой сложности.
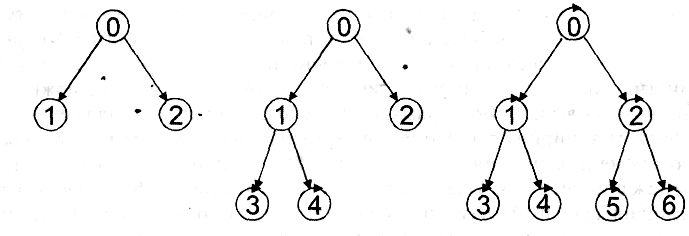
Рис. 4.1. Деревья поиска в ширину при l = 2: нулевая вершина
(дерево глубиной k = 0), дерево после нахождения последователей
нулевой вершины (дерево глубиной k = 1), дерево после нахождения
последователей первой вершины, дерево после нахождения
последователей второй вершины (дерево глубиной k = 2)
Если полагать, что получение каждого последователя требует одной единицы времени, то O(l k) является оценкой сложности по времени. В процессе поиска в ширину каждая вершина дерева должна сохраняться до получения требуемого решения. Если полагать, что для этого сохранения требуется единица памяти, то та же формула является одновременно и оценкой сложности по памяти для поиска в ширину.
Посмотрим, что это будут за величины при l=10 для различных значений k (табл. 4.1).
Предполагается, что 1000 вершин-последователей могут быть получены за 1 с, и что одна вершина требует 100 байт памяти. Эти значения соответствуют средним затратам времени и памяти, требуемым для решения многих иллюстративных задач типа головоломок. Из табл. 4.1 можно сделать два важных вывода.
Во-первых, рост требований к памяти для решения задач поиском в ширину гораздо более серьезная проблема, чем рост требований времени решения тех же задач. Табл.4.1
|
Глубина дерева |
Количество вершин |
Требуемое для поиска время |
Требуемая для поиска память |
|
0 |
1 |
1 миллисекунда |
100 байт |
|
2 |
111 |
0,1 секунды |
11 килобайт |
|
4 |
11.111 |
11 секунд |
1 мегабайт |
|
6 |
106 |
18 минут |
111 мегабайт |
|
8 |
108 |
31 час |
11 гигабайт |
|
10 |
1010 |
128 дней |
1 терабайт |
|
12 |
1012 |
35 лет |
111 терабайт |
|
14 |
1014 |
3500 лет |
11111 терабайт |
Так, например, вполне приемлемо подождать решения задачи в течение 18 мин при l = 6, но необходимость наличия 111 Мбайт памяти для решения таких сравнительно простых задач кажется слишком высокой ценой.
Во-вторых, для задач, в которых l > 10, помимо катастрофического увеличения требований к памяти, наблюдается стремительный рост временных затрат, не позволяющий решать реальные задачи с помощью поиска в ширину даже на современных мощных компьютерах. Это приводит к следующему заключению: Стратегии поиска, еющие экспоненциальные оценки сложности решения задач по времени и памяти, в частности стратегия поиска в ширину, нельзя использовать i решения задач большой размерности, т.е. задач, у которых 1 > 10.
4.2.2. Монотонный поиск в ширину
Поиск в ширину обеспечивает нахождение целевого состояния,
находящегося на минимальной глубине дерева поиска. Однако минимальность цены пути и этом не гарантируется. Монотонный поиск в ширину является некоторой модификацией поиска в ширину, заключающейся в том, что в процессе поиска в ширину всякий раз, когда определяется очередная вершина-последователь, одновременно вычисляется цена пути, ведущего в эту вершину. Эта цена пути используется для оценки целесообразности поиска вершин, продолжающих данный путь, сравнением с другими, уже полученными ценами путей.
Если цена данного пути меньше цен всех этих путей, то поиск вершин на этом пути продолжается. В противном случае поиск вершин на этом пути откладывается, а продолжается поиск вершин на путях, цена которых меньше данного. Когда на каком-либо пути будет достигнута целевая вершина, поиск на путях, цена которых выше цены этого пути, вообще прекращается. Все пути, имеющие одинаковую минимальную цену путей, ведущих в целевую вершину, являются решением задачи.
Вернемся к задаче поиска пути из Иванова в Москву. На рис. 4. 2, б схематически показана карта участка дорог, ведущих из Иванова в Москву. Каждая из дорог, ведущих из одного пункта в другой, снабжена числовой оценкой действия. На рис. 4.2, а показана последовательность монотонного поиска в ширину. Каждая из вершин помечена ценой пути, ведущего в эту вершину.
4.2.3. Поиск в глубину
При поиске в глубину, начиная с корневой вершины (корневая вершина находится на уровне 1), рассматриваются все инцидентные ей вершины уровня 2, начиная слева направо. Если удается найти среди них все целевые вершины, то на этом поиск прекращается. Если среди них не удается найти все целевые вершины, а максимальная глубина дерева еще не достигнута, то берется самая левая вершина уровня 2 и рассматриваются все инцидентные ей вершины уровня 3 слева направо. Если после этого все целевые вершины все еще не найдены, то берется самая левая вершина из уровня 3. Затем снова рассматриваются все инцидентные ей вершины уровня 3 слева направо, и так до тех пор, пока либо не будут найдены все целевые вершины, либо достигнута максимальная глубина дерева, на которой в соответствии с рассматриваемой процедурой просмотрены все вершины, инцидентные самой левой вершине предыдущего уровня, и все целевые все еще не найдены. В последнем случае осуществляется подъем по дереву на один уровень вверх, выбор на этом уровне самой левой вершины, инцидентные которой вершины следующего уровня еще не рассмотрены, и поиск дальше среди целевых вершин по тому же принципу. И так до тех пор, пока все вершины дерева не будут рассмотрены.
Р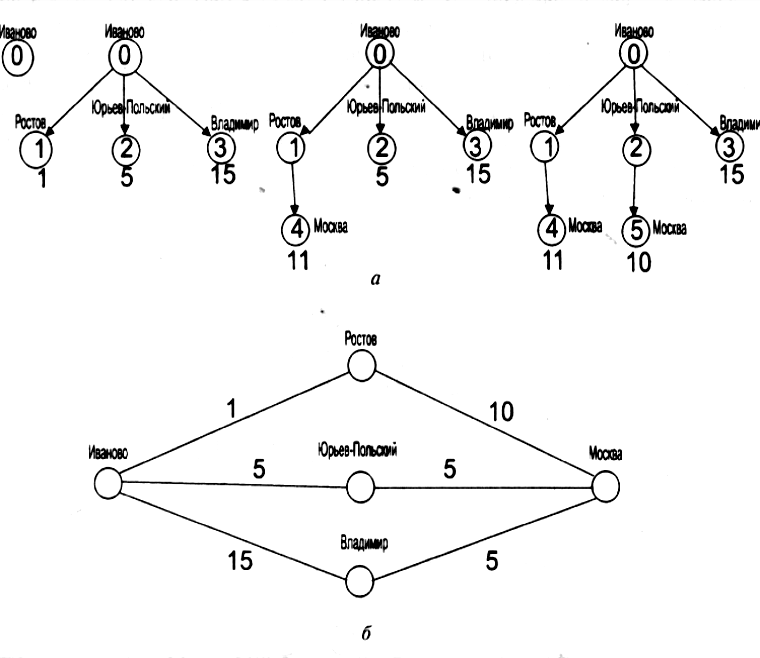 ис.
4. 2. Задача нахождения маршрута из Иванова
в Москву:
ис.
4. 2. Задача нахождения маршрута из Иванова
в Москву:
а - порядок монотонного поиска в ширину. Каждая вершина помечена ценой пути, ведущим в нее из начальной вершины (снаружи вершины) и номером ее получения в процессе поиска (внутри вершины). На последнем шаге монотонного поиска в ширину найдена целевая вершина с ценой пути, равным 10;
б- пространство состояний, иллюстрирующее цену действий, соответствующую участкам пути между городами.
Рис. 4.3. Стратегия поиска в глубину
На рис. 4.3 показана последовательность поиска в глубину для дерева с тремя уровнями и степенью ветвления 2. Вершины на этом рисунке пронумерованы в соответствии с последовательностью их просмотра.
Требования к объему памяти при поиске в глубину существенно меньше, чем при поиске в ширину. Как видно из рис. 4. 3, в памяти необходимо хранить все вершины, инцидентные вершинам на пути из корневой вершины к любой другой, соседние вершины которой рассматриваются. Очевидно, что при степени ветвления l и глубине дерева k оценка сложности по памяти при поиске в глубину равна O(lk). Оценка сложности по времени для поиска в глубину остается такой же, как и при поиске в ширину, а именно O(l k).
Для задач, дерево поиска для которых конечно, а число целей сравнительно невелико, поиск в глубину может оказаться эффективным, так как имеет шанс найти это небольшое число целей без просмотра всех вершин.
Для задач, имеющих большую или даже бесконечную глубину дерева, поиск в глубину может оказаться крайне неэффективным, так как будет стремиться все время в глубину, в то время как цель может оказаться близкой к корню дерева, но на том пути, который еще не был просмотрен. Поиск же все время уходит вниз и в случае бесконечной глубины дерева может никогда не вернуться назад к просмотру вершин, среди которых находятся целевые. Вследствие этого следует избегать использования поиска в глубину для решения задач с большой или бесконечной глубиной дерева. Поиск в глубину, таким образом, нельзя считать ни полным, ни оптимальным.
4.2.4. Ограниченный поиск в глубину
Ограниченный поиск в глубину является частным случаем поиска в глубину. При этом поиске используется ограничение на глубину поиска. Например, при поиске маршрута из Иванова в Москву при наличии информации о числе населенных пунктов, которые могут встретиться на этом пути, глубину поиска можно ограничить числом этих населенных пунктов. При ограниченном поиске в глубину, как только достигается уровень, совпадающий с этим числом, происходит возврат назад так же, как это делается при обычном поиске в глубину. Ограниченный поиск в глубину полный, если ограничение на глубину поиска выбрано таким образом, чтобы обеспечить просмотр всех вершин дерева. Оценки сложности по времени и памяти при ограниченном поиске в глубину те же, что и при обычном поиске в глубину.