ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Методичка
Дисциплина: Системы искусственного интеллекта
Добавлен: 29.10.2018
Просмотров: 337
Скачиваний: 8
ЛАБОРАТОРНАЯ РАБОТА №3.
ТЕМА: НЕЧЕТКИЕ МНОЖЕСТВА В МАТКАДЕ.
1.ФУНКЦИИ ПРИНАДЛЕЖНОСТИ. Как известно, принадлежность элемента данному нечеткому множеству определяется его функцией принадлежности. Ниже приведены примеры задания некоторых функций принадлежности .
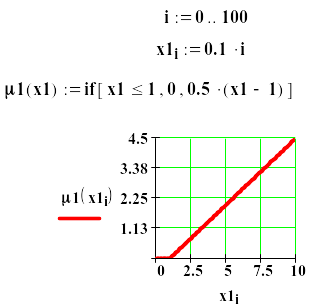Для задания функции принадлежности
используется функция маткада IF
(ЕСЛИ). В этой функции первое выражение
– условие, в данном примере – это x1<=1,
второе число – значение функции при
выполнении условия – в примере это 0,
третье число – значение функции при
невыполнении условия. В примере – это
0.5*(x1-1).График функции
принадлежности приведен на рисунке для
x1, меняющегося от 0 до 5.
Ниже приведены другие функции принадлежности и построены их графики.
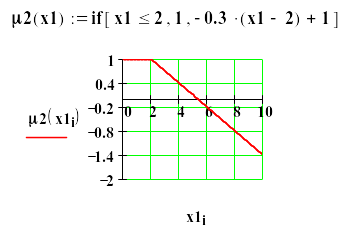
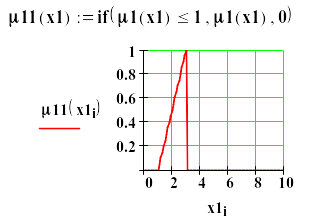
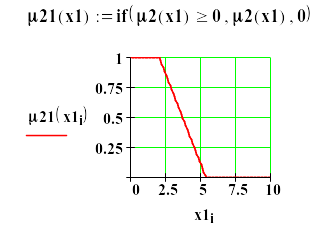
Рис.1. Различные функции принадлежности.
Если теперь присвоить х какое либо конкретное значение, то можно определить вероятность принадлежности этого значения тому или иному множеству. Например , положив х1=5, получим 1(х1)=2, 2(х1)=0.1и т.д.
ЗАДАНИЕ 1. Построить в маткаде приведенные выше функции принадлежности и их графики. Вычислить в маткаде значения всех функций принадлежности для х1=0,1,2,5,10.
2. ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ.
В теории множеств определены операции
пересечения и объединения множеств.
Пересечением
двух множеств А и В называется множество,
элементы которого принадлежат как
множеству А, так И множеству В.
Объединением
двух множеств А и В называется множество,
элементы которого принадлежат ИЛИ
множеству А ИЛИ множеству В. Ниже
показаны рисунки, иллюстрирующие эти
положения.
Рис.2. Объединение и пересечение двух множеств.
Здесь желтым цветом обозначено множество
А, сиреневым – множество В, синим -
пересечение
,
общий контур – объединение двух
множеств.
Для нечетких множеств, конечно, также существуют эти операции. Однако при этом меняются их функции принадлежности.
Если новое множество является пересечением двух нечетких множеств, его функция принадлежности является минимумом из функций принадлежности каждого из первоначальных множеств. Ниже приведены на одном графике функции принадлежности двух нечетких множеств, а рядом приведена функция принадлежности пересечения этих множеств, полученная как минимум каждого из двух исходных множеств.
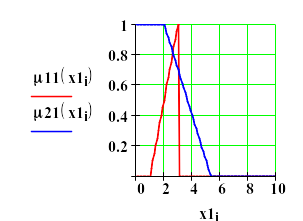
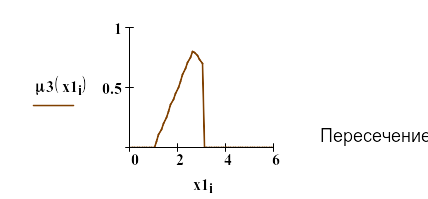
Рис.3. Функция принадлежности пересечения двух множеств.
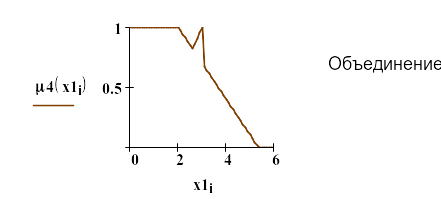
Функция принадлежности объединения двух нечетких множеств строится как максимальное значение функций принадлежности каждого из объединяемых множеств. Ниже на рис.4 приведены формула и график функции принадлежности объединения двух нечетких множеств, показанных в левой части рис.3.
Рис.4. Функция принадлежности объединения двух множеств.
ЗАДАНИЕ 2. Провести построение всех
приведенных выше функций принадлежности
и графиков.
3.МОДЕЛИРОВАНИЕ СЛОЖНЫХ
ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ.
Пусть необходимо смоделировать в маткаде функцию принадлежности, показанную н рисунке.
1
5 7 12 16 x
Аналитические выражения для нее написаны ниже.
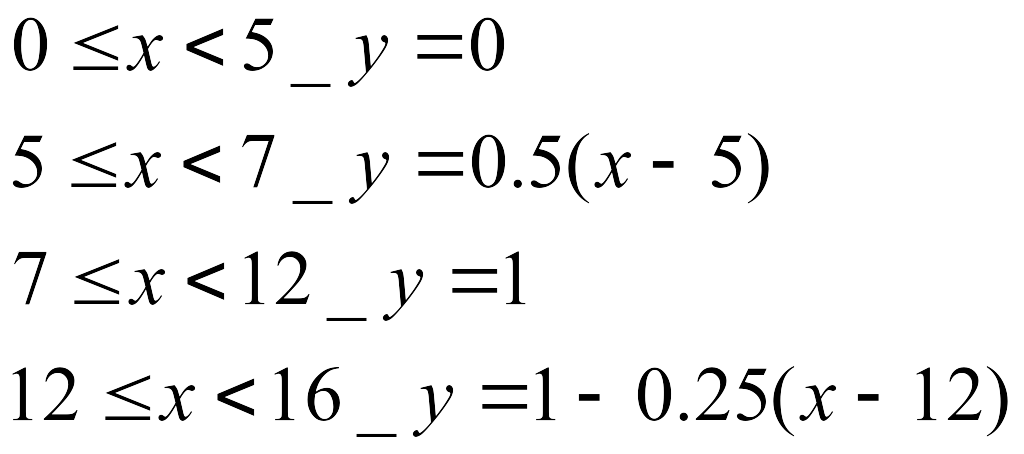
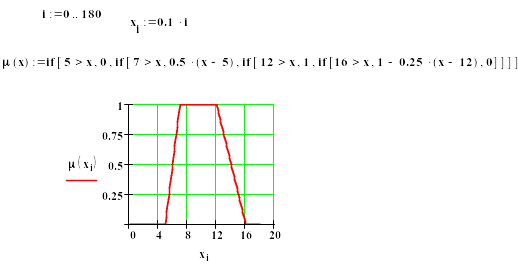
Такие функции в маткаде можно моделировать, используя вложенные функции IF, как показано ниже. Напоминаем, как выполняется функция IF: сначала записывается условие, затем через запятую, чему равно , если это условие выполняется, затем, снова через запятую, чему равно в случае невыполнения условия. Следовательно, формула
выполняется так:
Если 5>x, то равно 0. В противном случае, если 7> x=>5, =0.5(x-5). В случае, если 12>x=>7, =1. И, наконец, если 16>x=>12, то =1-0.25(x-12), а если 16<=x, то =0.
