Элементы дисперсионного анализа

2.1. Сравнение нескольких средних. Понятие о дисперсионном анализе

Дисперсионный анализ – статистический метод, предназначенный для выявления влияния отдельных факторов на результат эксперимента, а также для последующего планирования экспериментов.

Пусть генеральные совокупности распределены нормально и имеют одинаковую, хотя и неизвестную, дисперсию; математические ожидания также неизвестны, но могут быть различными. Требуется при заданном уровне значимости по выборочным средним проверить нулевую гипотезу о равенстве всех математических ожиданий. Другими словами, требуется установить, значимо или незначимо различаются выборочные средние. Казалось бы, для сравнения нескольких средних можно сравнить их попарно. Однако с возрастанием числа средних возрастает и наибольшее различие между ними: среднее новой выборки может оказаться больше наибольшего или меньше наименьшего из средних, полученных до нового опыта. По этой причине для сравнения нескольких средних пользуются другим методом, который основан на сравнении дисперсий и поэтому назван дисперсионным анализом (в основном развит английским статистиком Р. Фишером).

На практике дисперсионный анализ применяют, чтобы установить, оказывает ли существенное влияние некоторый качественный фактор F, который имеет p уровней на изучаемую величину X. Например, если требуется выяснить, какой вид удобрений наиболее эффективен для получения наибольшего урожая, то фактор F – удобрение, а его уровни – виды удобрений.

Основная идея дисперсионного анализа состоит в сравнении «факторной дисперсии», порождаемой воздействием фактора, и «остаточной дисперсии», обусловленной случайными причинами. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на X; в этом случае средние наблюдаемых значений на каждом уровне (групповые средние) различаются также значимо.

Если уже установлено, что фактор существенно влияет на X, а требуется выяснить, какой из уровней оказывает наибольшее воздействие, то дополнительно производят попарное сравнение средних.

Иногда дисперсионный анализ применяется, чтобы установить однородность нескольких совокупностей (дисперсии этих совокупностей одинаковы по предположению; если дисперсионный анализ покажет, что и математические ожидания одинаковы, то в этом смысле совокупности однородны). Однородные же совокупности можно объединить в одну и тем самым получить о ней более полную информацию, следовательно, и более надежные выводы.

В более сложных случаях исследуют воздействие нескольких факторов на нескольких постоянных или случайных уровнях и выясняют влияние отдельных уровней и их комбинаций (многофакторный анализ).

Мы ограничимся простейшим случаем однофакторного анализа, когда на X воздействует только один фактор, который имеет p постоянных уровней.

---

2.2.Общая факторная и остаточная суммы квадратов отклонений

Пусть на количественный нормально распределенный признак X воздействует фактор F, который имеет p постоянных уровней. Будем предполагать, что число наблюдений (испытаний) на каждом уровне одинаково и равно q.

Таблица 1

Номер испытания	Уровни фактора
			…
1 2 … q	…	…	… … … …	…
Групповая средняя			…

Пусть наблюдалось значений признака X, где i – номер испытания (j – номер уровня фактора ( Результаты наблюдений приведены в таблице 1.

Введем, по определению,

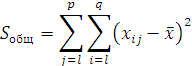
(общая сумма квадратов отклонений наблюдаемых значений от общей средней ),

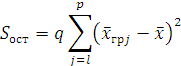
(факторная сумма квадратов отклонений групповых средних от общей средней, которая характеризует рассеяние «между группами»),

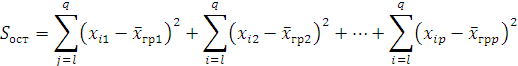
(остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней, которая характеризует рассеяние «внутри групп»).

Практически остаточную сумму находят по равенству:

Элементарными преобразованиями можно получить формулы, более удобные для расчетов:

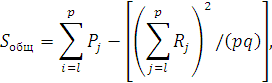
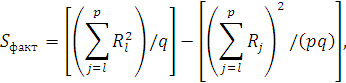
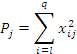
где – сумма квадратов значений признака на уровне

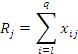
• сумма значений признака на уровне .

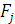Замечание. Для упрощения вычислений вычитают из каждого наблюдаемого значения одно и то же число C, примерно равное общей средней. Если уменьшенные значения , то

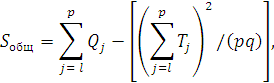
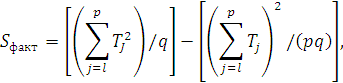
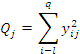
где – сумма квадратов уменьшенных значений признака на

уровне

– сумма уменьшенных значений признака на уровне

Для вывода формул и достаточно подставить

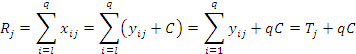
в соотношение и в

соотношение

Пояснения. 1. Убедимся, что характеризует воздействие фактора F. Допустим, что фактор оказывает существенное влияние на X. Тогда группа наблюдаемых значений при одном определенном уровне, вообще говоря, отличается от групп наблюдений на других уровнях. Следовательно, различаются и групповые средние, причем они тем больше рассеяны вокруг общей средней, чем большим окажется воздействие фактора. Отсюда следует, что для оценки воздействия фактора целесообразно составить сумму квадратов отклонений групповых средних об общей средней (отклонение возводят в квадрат, чтобы исключить погашение положительных и отрицательных отклонений). Умножив эту сумму на q, получим . Итак, характеризует воздействие фактора.

2. Убедимся, что отражает влияние случайных причин. Казалось бы, наблюдения одной группы не должны различаться. Однако, поскольку на X, кроме фактора F, воздействуют и случайные причины наблюдения одной и той же группы, вообще говоря, различны и, значит, рассеяны вокруг своей групповой средней. Отсюда следует, что для оценки влияния случайных причин целесообразно составить сумму квадратов отклонений наблюдаемых значений каждой группы от своей групповой средней, т.е. . Итак, характеризует воздействие случайных причин.

---

3. Убедимся, что отражает влияние и фактора и случайных причин. Будем рассматривать все наблюдения как единую совокупность. Наблюдаемые значения признака различны вследствие воздействия фактора и случайных причин. Для оценки этого воздействия целесообразно составить сумму квадратов отклонений наблюдаемых значений от общей средней, т.е. .

Итак, характеризует влияние фактора и случайных причин.

Приведем пример, который наглядно показывает, что факторная сумма отражает влияние фактора, а остаточная – влияние случайных причин.

Пример. Двумя приборами произведены по два измерения физической величины, истинный размер которой равен x. Рассматривая в качестве фактора систематическую ошибку C, а в качестве его уровней – систематические ошибки и соответственно первого и второго прибора, показать, что определяется систематическими, а – случайными ошибками измерений.

Решение. Введем обозначения: – случайные ошибки первого и второго измерений первым прибором; – случайные ошибки первого и второго измерений вторым прибором.

Тогда наблюдения значения результатов измерений соответственно равны (первый индекс при x указывает номер измерения, а второй – номер прибора):

Средние значения измерений первым и вторым приборами соответственно равны:

Общая средняя

факторная сумма

Подставив величины, заключенные в скобках, после элементарных преобразований получим

Мы видим, что определяется главным образом, первым слагаемым (поскольку случайные ошибки измерений малы) и, следовательно, действительно отражает влияние фактора C.

Остаточная сумма

Подставив величины, заключенные в скобках, получим

Мы видим, что определяются случайными ошибками измерений и, следовательно, действительно отражает влияние случайных причин.

Замечание. То, что порождается случайными причинами, следует также из равенства:

Действительно, является результатом воздействия фактора и случайных причин; вычитая мы исключаем влияние фактора. Следовательно, «оставшаяся часть» отражает влияние случайных причин.

---

Смотрите также файлы

• Лекция 1. Графический способ обработки опытных данных.doc

• Задание на контрольную работу №1.doc

• Лекция 3. Этапы проектирования.doc

• Лекция 2. Система, управление, информация.doc

• Лекция 1. Содержание информатизации управления.doc