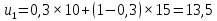Файл: Тема Функции и графики в экономическом моделировании Условие задания.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 66
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание 1
Тема 3. Функции и графики в экономическом моделировании
Условие задания. Постоянные издержки F, не зависящие от числа произведенной продукции х, составляют 135 тыс. руб. в месяц, а переменные издержки V – 750 руб. на каждую единицу продукции. Цена единицы продукции – 1300 руб. Найдите объем продукции х, при котором прибыль П равна 115 тыс. руб.
Рекомендации по выполнению задания
Решение задания следует произвести на основе представленного в бланке выполнения задания 1 алгоритма.
Бланк выполнения задания 1
Условие задания
Постоянные издержки F, не зависящие от числа произведенной продукции х, составляют 135 тыс. руб. в месяц, а переменные издержки V – 750 руб. на каждую единицу продукции. Цена единицы продукции – 1300 руб. Найдите объем продукции х, при котором прибыль П равна 115 тыс. руб.
Решение
-
Для определения объема продукции х необходимо построить линейное уравнение, увязывающее в зависимость приведенные в условии задачи показатели. При этом:
-
выручка представляет собой общий объем произведенной и реализованной продукции и определяется как произведение стоимости единицы продукции и общего объема произведенной продукции в натуральном выражении;
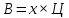
-
общая сумма затрат складывается из затрат постоянных и затрат переменных. Последние, в свою очередь, определяются как произведение суммы затрат, приходящейся на единицу произведенной продукции, и общего объема произведенной продукции в натуральном выражении;
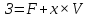
-
прибыль (П) = выручка (В) – затраты (З).
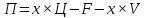
Прибыль равна 115000 руб. Подставим значения:
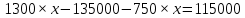
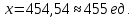
-
Вывод: объем продукции, при котором прибыль П равна 115 тыс. руб., составляет 454,54 ед., округлим до 455 ед.
Практическое задание 2
Тема 4. Дифференциальное и интегральное исчисление в экономическом анализе
Условие задания. Себестоимость производства телевизоров
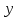 (в тыс. руб.) описывается функцией
(в тыс. руб.) описывается функцией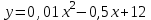 , где
, где 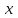 – объем выпускаемой продукции в месяц (тыс. ед.). Определите скорость и темп изменения себестоимости при выпуске продукции 20 тыс. ед. и 40 тыс. ед.
– объем выпускаемой продукции в месяц (тыс. ед.). Определите скорость и темп изменения себестоимости при выпуске продукции 20 тыс. ед. и 40 тыс. ед.Рекомендации по выполнению задания
Решение задания следует произвести на основе представленного в бланке выполнения задания 2 алгоритма.
Бланк выполнения задания 2
Условие задания
Себестоимость производства телевизоров
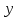 (в тыс. руб.) описывается функцией
(в тыс. руб.) описывается функцией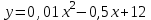 , где
, где 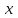 – объем выпускаемой продукции в месяц (тыс. ед.). Определите скорость и темп изменения себестоимости при выпуске продукции 20 тыс. ед. и 40 тыс. ед.
– объем выпускаемой продукции в месяц (тыс. ед.). Определите скорость и темп изменения себестоимости при выпуске продукции 20 тыс. ед. и 40 тыс. ед.Решение
1. Для решения задания воспользуйтесь следующим алгоритмом.
-
Для определения функции скорости изменения себестоимости найдем первую производную от заданной в условии функции.
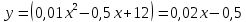
-
Для определения функции темпа изменения себестоимости найдем вторую производную от заданной в условии функции.
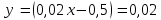
-
Подставим в полученные функции заданные в условии объемы выпуска продукции.
Скорость изменения себестоимости при выпуске продукции 20 тыс. ед. равна:
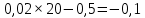
Скорость изменения себестоимости при выпуске продукции 40 тыс. ед. равна:
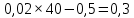
2. Вывод: скорость изменения себестоимости при выпуске продукции 20 тыс. ед. равна -0,1, при выпуске 40 тыс. ед. 0,3. Темп изменения себестоимости 0,02.
Практическое задание 3
Тема 7. Экономико-математическое моделирование
Условие задания. Провести процедуру краткосрочного прогнозирования спроса на некоторую услугу (млн руб.), используя процедуру сглаживания (по пяти точкам).
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Объем спроса, млн руб. | 10 | 15 | 20 | 15 | 30 | 25 | 30 | 40 | 45 | 50 | 60 | 65 |
Рекомендации по выполнению задания
Решение задания следует произвести на основе представленного в бланке выполнения задания 3 алгоритма.
Бланк выполнения задания 3
Условие задания. Проведите процедуру краткосрочного прогнозирования спроса на некоторую услугу (млн руб.), используя процедуру сглаживания (по пяти точкам) на основе данных, указанных в таблице.
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Объем спроса, млн руб. | 10 | 15 | 20 | 15 | 30 | 25 | 30 | 40 | 45 | 50 | 60 | 65 |
Решение
1. Для решения задачи используем следующие формулы:
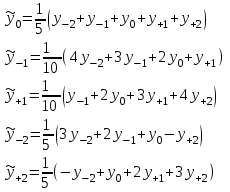
Первая формула позволяет определить сглаженные значения всех средних точек ряда (с 3-й по 10-ю), а оставшиеся формулы соответственно направлены на сглаживание крайних точек ряда (т. е. 2-й, 11-й, 1-й, 12-й точек соответственно).
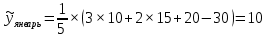
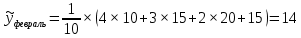
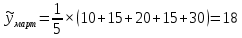
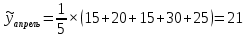
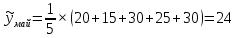
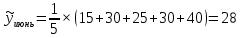
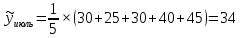
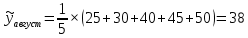
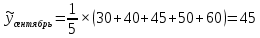
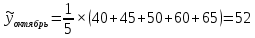
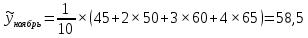
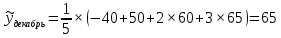
Построим графики. Для этого в системе координат по оси
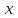 отложим порядковые номера месяцев, а по оси
отложим порядковые номера месяцев, а по оси 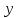 – объем спроса. В полученной системе координат построим два графика: первый – по фактическим значениям, представленным в условии, второй – по значениям, полученным в результате проведенных расчетов.
– объем спроса. В полученной системе координат построим два графика: первый – по фактическим значениям, представленным в условии, второй – по значениям, полученным в результате проведенных расчетов.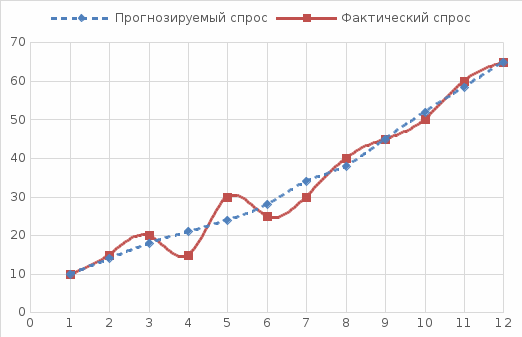
Практическое задание 4
Тема 7. Экономико-математическое моделирование
Условие задания. Рассчитать прогнозное значение по методу ЭВС на основе данных, приведенных в таблице с шагом прогнозирования, равным 1, и начальной оценкой U0 = 15. Расчеты следует провести при α = 0,2 и α = 0,3.
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Объем спроса, млн руб. | 10 | 15 | 20 | 15 | 30 | 25 | 30 | 40 | 45 | 50 | 60 | 65 |
Рекомендации по выполнению задания
Решение задания следует произвести на основе представленного в бланке выполнения задания 4 алгоритма.
Бланк выполнения задания 4
Условие задания. Рассчитать прогнозное значение, используя метод экспоненциально взвешенного среднего (ЭВС) на основе данных, приведенных в таблице, с шагом прогнозирования, равным 1, и начальной прогнозной оценкой U0 = 15. Расчеты следует провести при α = 0,2 и α = 0,3.
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Объем спроса, млн руб. | 10 | 15 | 20 | 15 | 30 | 25 | 30 | 40 | 45 | 50 | 60 | 65 |
Решение задания
При сглаживании временного ряда методом ЭВС используется следующая формула:
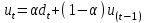 ,
,где
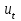 – прогнозное значение ЭВС;
– прогнозное значение ЭВС; 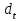 – фактическое значение показателей в момент t;
– фактическое значение показателей в момент t; 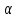 – параметр сглаживания; t – номер текущего периода;
– параметр сглаживания; t – номер текущего периода; 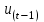 – прогнозное значение показателей в момент t.
– прогнозное значение показателей в момент t.При α = 0,2:
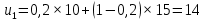
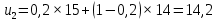
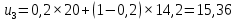
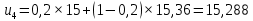
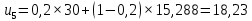
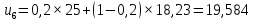
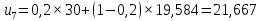
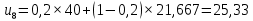
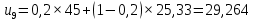
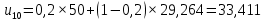
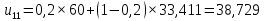
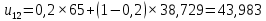
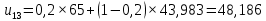
При α = 0,3: