Файл: otchyot3.docx

Нахождение обратной матрицы по схеме единственного деления Теория метода

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если ∆= 0. Матрица, обратная матрице А, обозначается через .

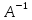Квадратная матрица называется обратной для квадратной матрицы А того же порядка, если их произведение А* =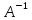*А = Е, где Е - единичная матрица того же порядка, что и матрицы А и .

Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Алгоритм решения задачи

Пусть дана неособенная матрица А=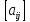 ( i, j = 1,2,…,n ) (1)

Для нахождения ее обратной матрицы (2) используем основное соотношение 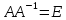(3) , где Е — единичная матрица.

Перемножая матрицы А и , будем иметьn систем уравнений относительно 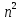неизвестных .

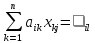( i, j = 1,2,…,n )

где

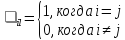
Полученные n систем линейных уравнений для j = 1,2,…,n , имеющих одну и ту же матрицу А и различные свободные члены, одновременно можно решить методом Гаусса.

Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А^-1. В результате умножения матриц должна получиться единичная матрица. Следовательно, вычисления произведены правильно.

Постановка задачи

Найти приближённо обратную матрицу для матрицы А с точностью до 0,001 по схеме единственного деления.

А=

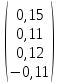
Решение

Для удобства поместим вычисления в таблицу .

Проверим правильность вычислений

А*A^-1= * =

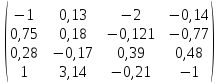Так как в результате умножения матриц получилась единичная матрица, следовательно, вычисления произведены правильно.

Нахождение определителя матрицы по схеме Гаусса Теория метода и алгоритм решения

Пусть

A= (1)

и ∆=detA (2)

Рассмотрим линейную систему Ax=0 (3)

При решении системы (3) по методу Гаусса мы заменяли матрицу А треугольной матрицей В, состоящей из элементов отмеченных строк

B=

В результате получалась эквивалентная система Bx=0 (4)

Элементы матрицы В последовательно получались из элементов матрицы А и дальнейших вспомогательных матриц , ,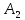… ,, с помощью следующих элементарных преобразований:

1. Деления на «ведущие» элементы 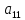, , … ,, 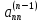которые предполагались отличными от нуля

2. Вычитания из строк матрицы А и промежуточных матриц 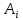( i=1,2, … , n-1 ) чисел, пропорциональных элементам соответствующих ведущих строк. При первой операции определитель матрицы также делится на соответствующий «ведущий» элемент, при второй— определитель матрицы остается неизменным. Поэтому

det B = 1 =

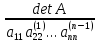
Следовательно,

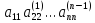∆ ==(5)

т. е. определитель равен произведению «ведущих» элементов для соответствующей схемы Гаусса. Отсюда заключаем, что приведенная схема единственного деления , в предыдущем методе, может быть использована для вычисления определителей, причем столбец свободных членов тогда становится излишним.

Заметим, что если для какого-нибудь шага элемент или близок к нулю (что влечет за собой уменьшение точности вычислений), то следует соответствующим образом изменить порядок строк и столбцов матрицы.

Постановка задачи

Найти приближенно определитель матрицы А с точностью до 0,0001 по схеме Гаусса.

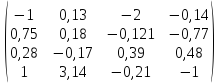
Решение

Для удобства поместим вычисления в таблицу