ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.03.2024
Просмотров: 121
Скачиваний: 0
Метод итераций (метод последовательных приближений) Теория метода и алгоритм решения
Пусть дана система n линейных уравнений с n неизвестными:
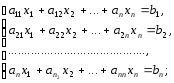 (1),
(1),
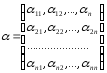
или в матричном виде: А · х = В (2), где:
А=( ),
), .
.
 ,
,
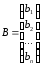 .
.
Предполагая,
что диагональные элементы
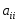
 0,
0, разрешим первое уравнение системы (1)
относительно
разрешим первое уравнение системы (1)
относительно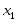 ,
второе – относительно
,
второе – относительно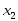 и т.д. Получим:
и т.д. Получим:
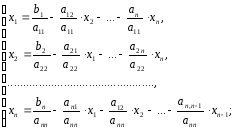 (2),
(2),
или:
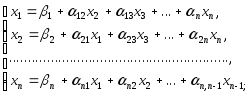 (3),
(3),
где:
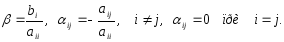
Система (3) называется системой, приведенной к нормальному виду.
Введя обозначения:
 ,
,
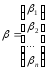 ,
,
запишем
систему (3) в матричной форме:
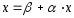 ,
или:
,
или:
 (4).
(4).
Решим систему (4) методом последовательных приближений. За нулевое приближение примем столбец свободных членов:
 .
.
Подставляя в (4) получим:
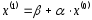 ,
,
затем:
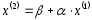 и т.д.
и т.д.
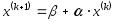 (5).
(5).
Итерации прерываются при выполнении условия:
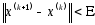 ,
где
,
где
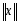 -
норма вектора,
-
норма вектора,
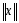 -max
-max
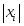 .
.
Теорема (условие сходимости итерационного процесса).
Если сумма модулей элементов строк или сумма модулей элементов столбцов меньше единицы, то процесс итераций для данной системы сходится к единственному решению, независимо от выбора начального приближения, т.е.:
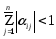 при
при
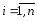 ,
,
или:
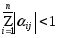 при
при .
.
На практике поступают следующим образом. Из заданной системы А · х = В выделяют уравнения с коэффициентами, модули которых больше или равны сумме модулей остальных коэффициентов уравнения. Каждое выделенное уравнение выписывают в такую строку новой системы, чтобы наибольший по модулю коэффициент оказался диагональным.
Из оставшихся использованных уравнений системы составляют между собой линейные комбинации с таким расчетом, чтобы был соблюден указанный выше принцип комплектования новой системы и все свободные строки оказались заполненными. При этом каждое использованное ранее уравнение должно попасть хотя бы в одну линейную комбинацию, являющуюся уравнением новой системы.
В итоге получаем преобразованную линейную систему, эквивалентную исходной и удовлетворяющей условию сходимости итерационного процесса.
Постановка задачи
Решить приближенно систему линейных уравнений с точностью до 0,001 методом итераций, предварительно преобразовав её к виду, подходящему для итераций.
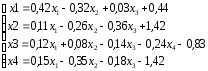
Решение
Преобразуем систему к виду, подходящему для итераций
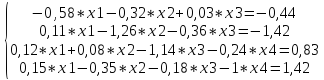
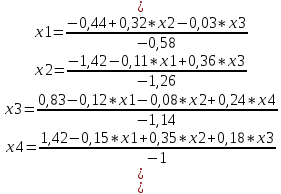
|
X1k |
X2k |
X3k |
X4k |
X1k+1 |
X2k+1 |
X3k+1 |
|
0,758621 |
1,126984 |
-0,72807 |
-1,42 |
0,099178 |
1,401233 |
-0,27018 |
|
0,099178 |
1,401233 |
-0,27018 |
-1,5696 |
-0,02845 |
1,212837 |
-0,28886 |
|
-0,02845 |
1,212837 |
-0,28886 |
-1,84692 |
0,074528 |
1,207031 |
-0,25713 |
|
0,074528 |
1,207031 |
-0,25713 |
-1,79677 |
0,079373 |
1,206956 |
-0,25725 |
|
0,079373 |
1,206956 |
-0,25725 |
-1,785 |
0,079408 |
1,207415 |
-0,25923 |
|
0,079408 |
1,207415 |
-0,25923 |
-1,78422 |
0,079052 |
1,207982 |
-0,25935 |
|
X4k+1 |
X1k+1-X1k |
X2k+1-X2k |
X3k+1-X3k |
X4k+1-X4k |
max |
Конец |
|
-1,5696 |
0,659443 |
0,274249 |
0,457889 |
0,149599 |
0,659443 |
No |
|
-1,84692 |
0,127626 |
0,188396 |
0,018675 |
0,277324 |
0,277324 |
No |
|
-1,79677 |
0,102977 |
0,005806 |
0,031729 |
0,050156 |
0,102977 |
No |
|
-1,785 |
0,004845 |
7,54E-05 |
0,000127 |
0,011767 |
0,011767 |
No |
|
-1,78422 |
3,5E-05 |
0,000459 |
0,001973 |
0,000776 |
0,001973 |
No |
|
-1,78402 |
0,000355 |
0,000567 |
0,000127 |
0,0002 |
0,000567 |
Yes |
Проверка:
|
-0,44021 |
|
-1,41929 |
|
0,829955 |
|
1,419771 |
Вывод
Из рассмотренных в данной лабораторной работе методов наиболее выгодным я считаю метод Гаусса, не требующий многочисленных шагов для нахождения неизвестных. Он легок в реализации и подходит для решения любой системы линейных уравнений, нахождения обратной матрицы и определителя. Единственным условием является то, что исходная матрица должна быть невырожденной, т. е. её определитель не равен нулю.