Файл: физика методичка.doc

ВВЕДЕНИЕ

Основная задача лабораторных работ заключается в закреплении и углублении теоретических знаний, полученных студентами на лекциях, в приобретении ими навыков проведения экспериментальных измерений, обработки полученных данных и оценки погрешностей.

При выполнении лабораторных работ необходимо соблюдать правила техники безопасности согласно инструкции №11а.

При выполнении лабораторных работ каждый студент должен иметь отчет о выполнении лабораторной работы и рабочий журнал.

Отчет о выполнении лабораторной работы должен содержать:

1. Введение.Краткое описание теории явления или метода.

2. Описание установки.Описание экспериментальной установки с приведением принципиальной или электрической схемы.

3. Порядок выполнения измерений.Таблицы экспериментальных данных и расчетных значений.

4. Обработка результатов измерений.Записываются расчетные соотношения в общем виде, а затем делается подстановка численных значений и определяется результат. Графики выполняются на миллиметровой бумаге.

5. Вывод (заключение).Содержит окончательные результаты и вывод о проделанной работе.

Требования пп. 1-3, включая таблицы для экспериментальных и расчетных данных, необходимо оформить во время самостоятельной подготовки к работе.

В рабочем журнале указываются номер и тема выполняемой лабораторной работы, а также таблицы для экспериментальных и расчетных значений. Рабочий журнал оформляется во время самостоятельной подготовки к лабораторной работе.

Лабораторная работа № 1.1

Определение объема цилиндра

Цель работы:научиться производить измерения с помощью штангенциркуля и микрометра, а также освоить способы обработки результатов измерений.

Введение

При выполнении лабораторных работ студент должен овладеть методами измерения физических величин и математической обработки результатов измерений.

Измерение физической величины заключается в сравнении ее с другой однородной физической величиной, принятой за единицу. Различают два вида измерений: прямые и косвенные.

1) Прямые измерения– это такие измерения, когда искомая величина определяется непосредственно с помощью инструмента или прибора, шкала которого проградуирована в единицах измерения определяемой величины. Прямые измерения бывают двух типов:

а)прямые единичные (однократные) измерения– это такие измерения, при которых их повторение дает один и тот же результат или, по условиям опыта, повторить измерение невозможно;

б)прямые многократные измерения– это такие измерения, при которых их повторение дает разные результаты. Число повторных измеренийnназываетсявыборкой.

2) Косвенные измерения – это такие измерения, когда искомая величина вычисляется по данным прямых измерений по соответствующим функциональным зависимостям, устанавливающим связь между искомой величиной и этими прямыми измерениями.

Измерить абсолютно точно принципиально невозможно по следующим причинам:

а) невозможно изготовить абсолютно точный прибор в связи с погрешностями изготовления;

б) приборы изнашиваются, стареют, в результате чего их точность уменьшается;

в) силы взаимодействия (силы трения, тяжести и т.д.) и внешние факторы (температура окружающей среды, давление, влажность, электрические и магнитные поля) изменяют измеряемые параметры тел, сред и влияют на характеристики приборов;

г) измеряемые параметры часто изменяются в пространстве и во времени, например, диаметр проволоки или температура помещения;

д) точность измерения зависит от квалификации экспериментатора.

Влияние этих факторов приводит к возникновению погрешностей измерений. Все погрешности делятся на две группы:

а) систематические погрешности– это такие погрешности, когда при повторении измерений величина и знак погрешности остаются неизменными. Например, часы каждые сутки «уходят вперед» на 10 секунд;

б) случайные погрешности– это такие погрешности, когда при повторении измерений величина и знак погрешности изменяются хаотически. Случайные погрешности возникают вследствие неоднозначности измеряемых параметров в пространстве и времени, а также влияния внешних факторов. Например, диаметр проволоки случайно изменяется по ее длине в обе стороны относительно среднего значения.

Для оценки точности выполненных измерений рассчитываются абсолютная и относительная погрешности.

Абсолютной погрешностью измерения Δх_иназывается разница между истинным и измеренным значениями искомой величины, измеряемая в тех же единицах, что и измеряемая величина:

Δх_и =х_и –х.

Однако абсолютная погрешность недостаточно полно характеризует точность измерения. Если расстояние между городами и длину карандаша измерить одним и тем же прибором, то точность измерений в первом случае будет намного выше. В связи с этим вводится понятие относительной погрешности.

Относительной погрешностью называется отношение абсолютной погрешности к измеренной величине, измеряется в процентах:

.

Так как истинное значение физической величины определить невозможно, то за результат измерений принимается действительное значениефизической величиных_д, которое определяется тем или иным способом в зависимости от вида измерений и объёма выборки. Действительное значение физической величины будет сколь угодно близко приближаться к истинному значению только при бесконечно большой выборке (n→ ∞). Поскольку практически выборки содержат конечное (и, как правило, небольшое число измеренийn) между действительным и истинным значениями существует различие, определить которое невозможно. Однако возможно определить интервал значений измеряемой величиных_д± Δх, называемыйдоверительным интервалом, в который истинное значение измеряемой величины попадает с известной вероятностью α, называемойнадежностью доверительного интервала. Величина Δхназываетсяграницей доверительного интервала.

Определение погрешностей прямых единичных измерений

1. За действительное значение принимается измеренное значение физической величины:

х_д =х.

2. В качестве границ доверительного интервала принимается абсолютная погрешность, которая вычисляется:

а) по классу точности прибора. Класс точности kявляется технической характеристикой прибора и указывается на панели прибора или в его техническом паспорте:

где Х_пред– предел измерения прибора, т.е. наибольшая величина, которую прибор способен измерить;

б) по цене деления прибора. Если у прибора не указан класс точности (например, линейка, термометр), то в качестве абсолютной погрешности берут цену деления прибора.

3. Относительная погрешность определяется по формуле:

.

4. Надежность доверительного интервала принимаем равной единице:  = 1

5. Окончательный ответ записывается в виде:

х = (х_д ± Δх) единицы измерения с ε% ( = 1).

Определение погрешностей прямых многократных измерений

1. За действительное значение принимается среднее значение физической величины:

х_д =.

Пусть неизвестную величину измерили nраз:

х_i=х₁,х₂,х₃,…,х_n.

Тогда среднее значение определяется по формуле:

,

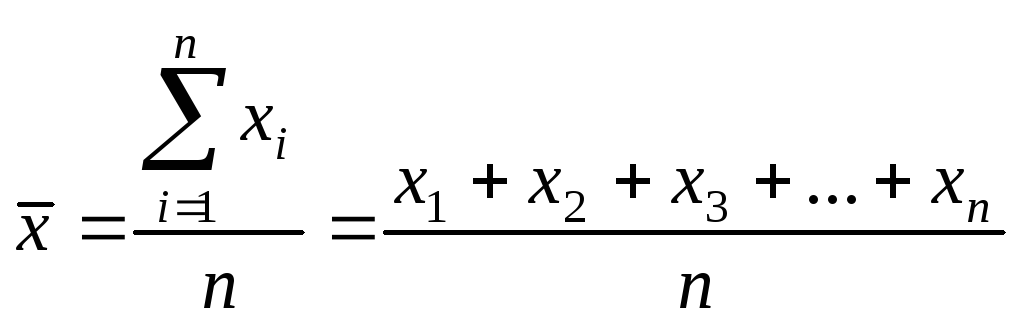где n– число измерений.

2. Определяют абсолютную погрешность каждого измерения:

Δх_i=.

3. Вычисляют среднеквадратичную погрешность среднего арифметического значения (стандарт):

.

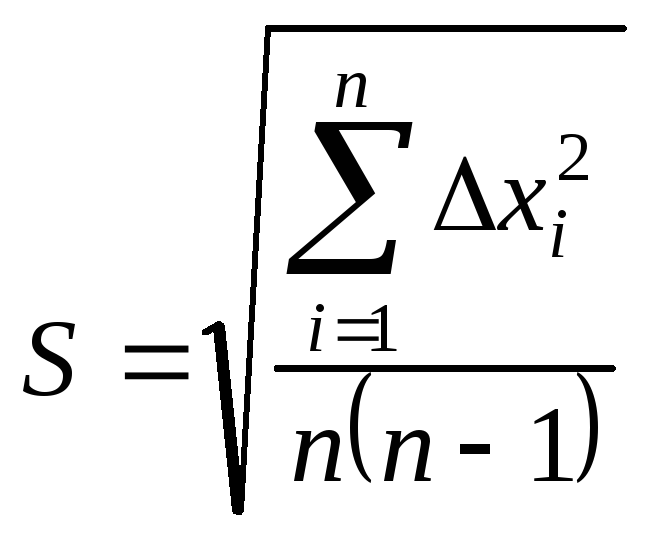4. Надежность доверительного интервала принимаем равной 0,9. По числу измерений и надежности определяют коэффициент Стьюдента t_α(n).

5. Вычисляют случайную ошибку измерений:

Δх_случ = S·t_α(n).

6. Определяют приборную ошибку (см. первый способ п.2 (а,б)).

7. Вычисляют абсолютную суммарную погрешность по формуле:

Δх= Δх _случ+ Δх _приб,

которую принимают за границу доверительного интервала.

8. Относительная погрешность определяется по формуле:

.

9. Окончательный ответ записывается в виде:

х = (х_д ± Δх) единицы измерения с ε % ( = 0,9).

Определение погрешностей косвенных измерений

Погрешность косвенного измерения складывается из погрешностей прямых измерений. Определение погрешностей косвенных измерений можно проводить двумя способами.

Первый способ.

1. За действительное значение принимается рассчитанное по формуле значение физической величины:

х_д =F(а_д,b_д…),

где а_д,b_д– действительные значения прямых измерений.

2. Вычисляют частные производные функции F:

3. Вычисляют абсолютные погрешности прямых измерений, входящих в исходную функцию F: Δа, Δb…

Если в расчетной формуле для х_диспользуется величина, взятая из таблицы, или округленная математическая константа, то при расчетехследуетучитывать погрешность табличной величины. За погрешность табличной величины принимают половину разряда последней значащей цифры числа.

Например: