Файл: Информатика и программирование.pdf

Рассмотрим, в первую очередь, алгоритмы внутренней сортировки данных. Как уже было сказано, алгоритмы внутренней сортировки работают только с данными, которые находятся во внутренней памяти ЭВМ. И именно поэтому, при выборе рассматриваемых алгоритмов сортировки данных отдается предпочтение тем алгоритмам, которые экономят эту память, то есть в первую очередь, рассматривается эффективность алгоритма.[9] Эту эффективность можно определить при подсчете количества сравнений ключей и пересылок сортируемых элементов.

Для начала, необходимо рассмотреть простые алгоритмы внутренней сортировки данных, так как они очень легки в использовании и в обучении. Программы, которые создаются при помощи этих простых алгоритмов сортировки, работают лишь в массивах с малым количеством элементов, но они очень быстры и эффективны в своей работе, следовательно, с их помощью молодые начинающие программисты легко получат неисчерпаемый багаж знаний, и затем, научатся работать с более сложными алгоритмами сортировки. Простыми алгоритмами внутренней сортировки данных считаются: сортировка обменом (метод пузырька), сортировка выбором, сортировка включением. Рассмотрим их подробно.

2.1 Сортировка методом пузырька (обменом)

Как уже было сказано, сортировка методом пузырька считается наиболее простым алгоритмом сортировки. Для лучшего понятия определения этого алгоритма можно представить себе сосуд, наполненный газированной водой. Самые тяжелые пузырьки воздуха всплывают наверх сосуда, а самые легкие остаются на дне. Так и алгоритм сортировки работает таким образом, что «тяжелые» элементы оказываются наверху массива, а «легкие» остаются внизу.[14] Каждый элемент массива сравнивается с другим элементом, и если один из них окажется «тяжелее» другого, то они меняются местами. Если в массиве будет найден самый большой элемент, то он будет считаться главным элементом, и все остальные элементы будут сравниваться с ним. Это сравнение будет происходить до тех пор, пока этот «тяжелый» элемент не окажется на вершине массива.

Рассмотрим, на примере, как работает данные алгоритм внутренней сортировки данных:

Как уже известно, суть данного алгоритма заключается в том, чтобы максимальный элемент массива оказался в конце массива. Работа алгоритма начинается в том, что он разбивает массив на группы элементов и сравнивает их поочередно между собой. Как видно, первая пара элементов не требует перестановки, также как и второй элемент не является больше третьего. Далее сравниваются элементы «16» и «5». Четвертый элемент меньше элемента «16», следовательно, их необходимо поменять местами. Следующий элемент «7» меньше – меняем местами, «10» меняем местами с «16», и последний шаг – элемент «3» требует смены позиций с элементом «16». По итогу всей работы алгоритма максимальный элемент «16» оказался в конце рассматриваемого массива.

На рисунке 7 показана блок схема работы алгоритма сортировки методом пузырька:

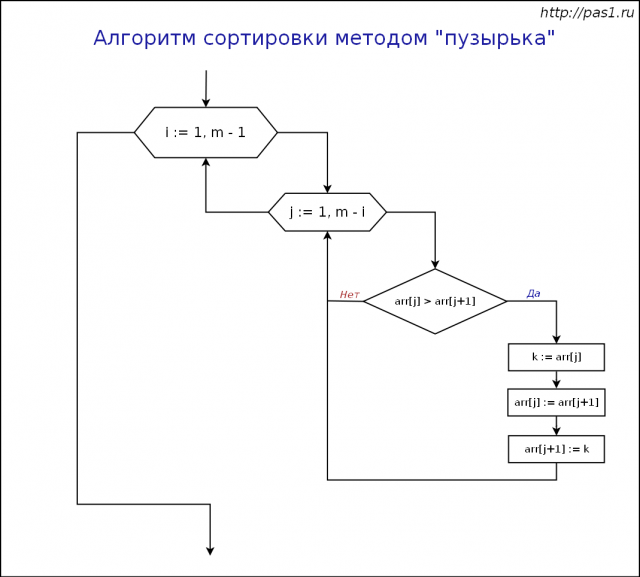
Рис. 7. Блок схема алгоритма

Приведем пример программы для сортировки методом пузырька на рисунке 8:

Рис. 8. Листинг алгоритма сортировки методом пузырька

У данного метода сортировки есть один существенный недостаток – массив, над которым проводилась работа, в конечном итоге оказывается не до конца отсортированным. Максимальный элемент массива оказывается в конце, но остальные элементы не считаются упорядоченными. При сортировке массивов с малым количеством элементов этот недостаток может оказаться незамеченным, но в больших массивах это может привести к затруднениям для пользователей. Для решения этой проблемы программисты усовершенствовали данный метод, и назвали его алгоритмом шейкер-сортировки. Этот алгоритм в процессе своей работы не только добивается того, что максимальный элемент оказывается в конце массива, но и сортирует остальные элементы в порядке возрастания, что очень удобно для пользователей.[15] По итогу своей работы он упорядочивает элементы массива следующим образом:

Программа в Pascal для шейкер-сортировки:

Рис. 9. Листинг шейкер-сортировки

Алгоритм шейкер-сортировки считается доработанным вариантом алгоритма сортировки методом пузырька.

2.2. Сортировка с помощью выбора

Сортировка с помощью выбора очень удобна в использовании, и в конце ее работы самый «большой» элемент массива окажется в конце массива. Данный алгоритм выбирает в массиве элемент с наименьшим значением, и производит его перестановку с элементом, который находится в начале массива, следовательно, сортировка с помощью данного алгоритма происходит по возрастанию. Рассмотрим по таблице, пример того, как происходит этот процесс перестановки элементов:

Как видно на таблице, массив отсортирован в порядке возрастания, но у данного алгоритма есть один существенный недостаток – в связи с тем, что в результате своей работы алгоритм выполняет несколько проходов по всему массиву, в поисках элемента с наименьшим значением, он затрачивает на это много времени, следовательно, он выполняет свою работу гораздо медленнее рассмотренного выше алгоритма сортировки. [5]

На рисунке 10 показана блок схема алгоритма внутренней сортировки выбором:

Рис. 10. Алгоритм сортировки выбором

Для лучшего понимания работы алгоритма сортировки выбором необходимо привести пример программного листинга алгоритма:

Рис.11. Листинг программы

Итак, данный алгоритм сортировки очень эффективен при работе с массивами, которые имеют малое количество элементов.

2.3. Алгоритм сортировки включением

Последний из простых алгоритмов сортировки – это сортировка простым включением. Идея данной сортировки заключается в том, что элемент сравниваются между собой, можно сказать в логической последовательности, например, сначала сравнивается первая пара элементов, после их упорядочения с ними сравнивается третий элемент массива. [17] В итоге, каждый элемент массива занимает свое место, и сортировка происходит по возрастанию. Для лучшего понимания данного определения необходимо рассмотреть следующую таблицу:

Как видно в таблице, данный алгоритм сортировки данных очень эффективен в упорядочивании элементов массива, но такой алгоритм работает очень быстро в уже практически отсортированном массиве данных. Чем меньше количество проходов в массиве, тем быстрее данный алгоритм выполняет свою работу. Но как уже было сказано, простые алгоритмы сортировок данных, эффективны только в массивах с малым количеством элементов. В массивах с большим количеством элементов они будут работать очень долго, потребуют выделения дополнительной памяти и многое другие неприятные для пользователя ситуации. Но, как уже было сказано, на их основе созданы усовершенствованные алгоритмы внутренней сортировки, которые быстро и легко справляются с большими массивами данных.

На рисунке 12 показана блок схема алгоритма сортировки включением:

Рис.12. Блок схема алгорима сортировки включением

Для того, чтобы более ясно понять как именно производит свою работу алгоритм сортировки включением необходимо рассмотреть листинг программы данной сортировки:

Рис. 13. Листинг сортировки включением

2.4. Сортировка Шелла

Рассматриваемый алгоритм сортировки был изобретен программистом Дональдом Шеллом в 1959 году, и получил свое название в честь своего изобретателя.[7] этот алгоритм выполняет свою работу в несколько проходов. Сначала он сравнивает элементы, которые находятся друг от друга на расстоянии, предположим, 8 позиций, затем, при втором проходе сравниваются элементы, которые располагаются друг от друга на расстоянии, например, 4 позиции. На последнем проходе, данный алгоритм просто упорядочивает оставшиеся неотсортированные элементы между собой. Для лучшего понятия работы данного алгоритма сортировки, рассмотрим следующий пример:

На данной таблице видно, что алгоритм сортировки методом Шелла выполнил свою работу за три прохода по массиву. Зрительно можно сказать, что алгоритм разбивает массив на группы. В данном случае группа «7 и 5» произвела смену мест с группой «4 и 3». Массив уже выглядит упорядоченным, следующий шаг, смена мест между собой элементов «4» и «2», а также элементов «7» и «6». На последнем шаге, алгоритм лишь произвел смену мест двух элементов, которые находились не на своем месте – это элементы «6» и «5».

Эффективность данного алгоритма сортировки данных заключается в том, что он не манипулирует в процессе своей работы всем элементами массива, а упорядочивает их группами, на некотором определенном шаге. Пользователям может показаться, что в этом случае данный алгоритм работает медленнее рассмотренных выше алгоритмов сортировок, но на самом деле он работает достаточно быстро, так как массив упорядочивается на каждом проходе алгоритма.