Файл: Аэропорт (Имитационная модель).pdf

Введение

Требуется построить имитационную модель объекта, описываемого следующим образом:

Аэропорт

Самолеты прибывают для посадки в район аэропорта каждые 5±2 минуты. Если взлетно-посадочная полоса свободна, прибывший самолет получает разрешение на посадку. Если взлетно-посадочная полоса занята, самолет выполняет полет по кругу и возвращается в аэропорт через 4 мин. Если после пятого круга он не получает разрешения на посадку, то отправляется на запасной аэродром. В аэропорту каждые 10±2 мин к взлетно-посадочной полосе выруливают готовые к взлету самолеты и получают разрешение на взлет, если полоса свободна. Время взлета и время посадки (нахождение на полосе) составляют каждое 2 мин. Если при свободной полосе одновременно один самолет прибывает для посадки, а другая – для взлета, полоса предоставляется взлетающему самолету.

Необходимо смоделировать работу аэропорта в течение суток и определить:

– число взлетевших самолетов;

– число самолетов, совершивших посадку;

– число самолетов, ушедших на запасной аэродром;

– коэффициент загрузки взлетно-посадочной полосы.

Важность моделирования в данной ситуации объясняется тем, что обычно модели строятся для объектов, которые ещё только проектируются и реально не существуют, либо предполагается модернизация или изменение режима функционирования уже существующего объекта. Аэропорт является очень дорогостоящей системой, проведение экспериментов с которым в реальности приведёт к большим затратам материальных ресурсов. Кроме того, необходимо учитывать, что функционирование аэропорта обычно связано с обслуживанием людей, что накладывает дополнительные ограничения на проведение натурных экспериментов. Поэтому проведение экспериментов на модели и получение на ней экспериментальных данных оправдано.

Моделируемым объектом в нашем случае является взлётно-посадочная полоса аэропорта с позиции приёма на посадку и разрешения взлёта самолётам.

Данная полоса может быть рассмотрена как обслуживающий прибор в системе массового обслуживания [1], а самолёты – как требования на обслуживание. При этом самолёты имеют разные приоритеты на обслуживание: отлетающие более приоритетны по сравнению с прилетающими.

Основными проблемами, которые необходимо решить, являются оценки загруженности взлётно-посадочной полосы и количество самолётов, не принятых аэропортом (ушедших на запасной аэродром). Загруженность может быть представлена числом от 0 до 1, показывающим долю общего времени моделирования, в течение которого полоса была занята. Количество непринятых самолётов – целое число. Для корректности выводов, необходимо также знать количество взлетевших самолётов и совершивших посадку.

---

Доступными для исследователя данными являются характеристики полосы (время, отводимое на взлёт и посадку одного самолёта), интенсивность прибытия и отлёта самолётов, поведение самолёта в случае отказа в посадке.

Целью исследования является определение:

– числа взлетевших самолетов;

– числа самолетов, совершивших посадку;

– числа самолетов, ушедших на запасной аэродром;

– коэффициента загрузки взлетно-посадочной полосы.

1. Основная часть

Обзор подходов

Решение поставленных задач возможно различными способами. Наиболее распространёнными являются: натурный эксперимент, построение и анализ математической модели, работа с имитационной моделью.

Первый способ (натурный эксперимент) в описанной задаче является труднореализуемым. Для этого необходимо иметь аэропорт с указанными в задании характеристиками и обеспечить требуемый поток самолётов на взлёт и посадку. Кроме того, сам процесс получения такого идеального (для анализа проблемы) объекта сопряжён с большими финансовыми затратами и моральными издержками, поскольку затрагивает интересы большого числа людей (пассажиров).

Второй способ предполагает использование некоторой математической модели системы массового обслуживания. Для описанного процесса функционирования аэропорта имеющиеся ныне модели [1] не могут быть непосредственно применены, поскольку не учитывают изменения характера потока требований во времени. Это изменение связано с наличием повторного захода самолёта на посадку при первичном отказе. Поэтому здесь требуется строить новую математическую модель. Но наличие обратной связи (повторные заходы самолёта на посадку) приводит к сложным математическим построениям, требующим больших временных и интеллектуальных затрат.

При создании имитационной модели проблемы, связанные с получением аналитического вида законов распределения при повторных заходах самолёта на посадку решаются имитацией указанного процесса. Этим обходятся проблемы сложности математических выкладок, присущих математическому моделированию. А, поскольку исследование проводится на компьютере, то исчезают расходы на натурные эксперименты с реальным аэропортом.

Обоснование выбора

---

В отсутствии возможности проводить эксперименты с реальным аэропортом и сложностью проведения математических преобразований описанных процессов при построении аналитической модели, разумным представляется выбор в качестве метода исследования заявленной системы применение имитационного моделирования.

Поскольку данный объект является системой массового обслуживания, то адекватным инструментом его моделирования является язык GPSS World [2]. В нём реализованы многочисленные средства представления моделей с разнообразными вероятностными законами распределения как входящих потоков, так и времени обслуживания требований. Встроенные инструменты статистической обработки позволяют автоматически получать результаты моделирования, интересующие исследователя.

2. Имитационная модель

При построении модели сделаем следующие предположения.

1. Единицей модельного времени является 1 минута.
2. Рассматриваются только моменты времени, когда прилетающий самолёт уже готов совершить приземление. Эти моменты наступают через случайные временные интервалы, распределённые согласно равномерному закону распределения на интервале 5±2 минуты.
3. При выходе на позицию готовности приземления, самолёт получает информацию о том, свободна ли взлётно-посадочная полоса. Если свободна, то он тут же совершает посадку, занимая её на 2 минуты. Если занята, то он уходит на полёт по кругу.
4. После завершения полёта по кругу в течение 4 минут, самолёт снова выходит на позицию готовности приземления, и получает сведения о том, свободна ли взлётно-посадочная полоса. Дальнейшие действия происходят в соответствии с описанием п.3.
5. Если самолёт не смог приземлиться, совершив пять кругов, то он уходит на запасной аэродром.
6. Рассматриваются только моменты времени, когда улетающий самолёт уже готов ко взлёту. Эти моменты наступают через случайные временные интервалы, распределённые согласно равномерному закону распределения на интервале 10±2 минуты.
7. При выходе на позицию готовности взлёта, самолёт получает информацию о том, свободна ли взлётно-посадочная полоса. Если свободна, то он тут же совершает взлёт, занимая её на 2 минуты. Если в этот же момент прилетает самолёт, то взлетающий всё равно занимает взлётно-посадочную полосу, т.е. он имеет больший приоритет.
8. Моделирование прекращается через 1440=24*60 минут модельного времени, в течение которого постоянно справедливы указанные выше предположения.

---

Для описанных предположений можно составить модель на языке GPSS, граф которой представлен на рис. 1.

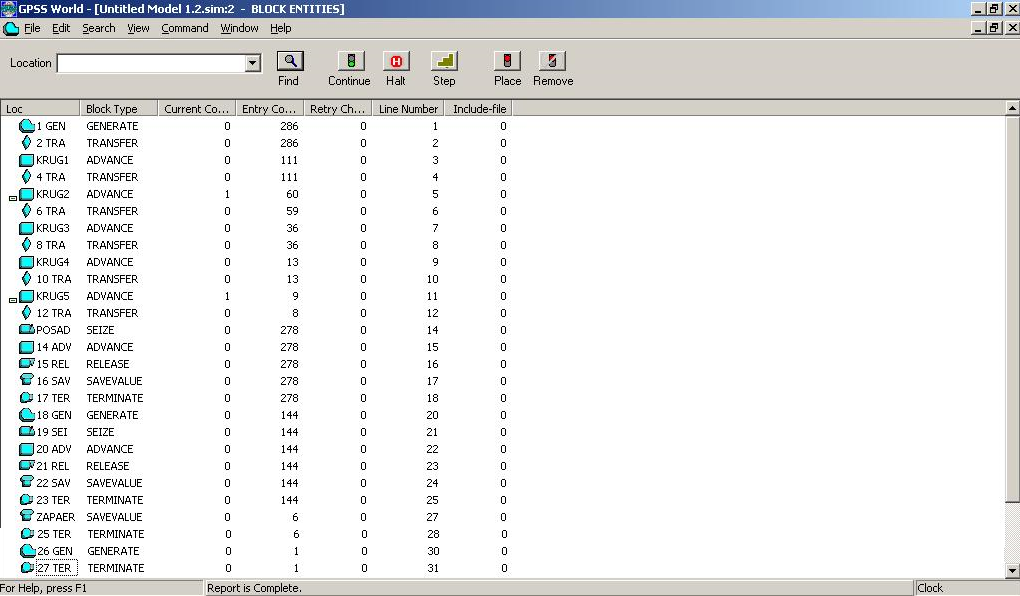
Рисунок 1 Граф модели в виде копии экрана с графом блок-схемы GPSS.

Логика протекания модельных процессов может быть описана следующим образом.

В модели имеются два сегмента, отвечающие собственно за моделирование эксплуатации взлётно-посадочной полосы, и один сегмент, отвечающий за время моделирования.

В первом сегменте возникают транзакты, соответствующие прилёту самолётов к аэропорту. Транзакты имеют приоритет 0 (самый низкий). При возникновении транзакта он проверяет наличие возможности приземлиться. Если она предоставляется (взлётно-посадочная полоса свободна), то он уходит на посадку, занимая её. Если это не так, то он уходит на первый круг, который занимает 4 минуты. После этого он проверяет наличие возможности приземлиться. Если она предоставляется (взлётно-посадочная полоса свободна), то он уходит на посадку, занимая её. Если это не так, то он уходит на второй круг, который занимает 4 минуты. После этого он проверяет наличие возможности приземлиться. Если она предоставляется (взлётно-посадочная полоса свободна), то он уходит на посадку, занимая её. Если это не так, то он уходит на третий круг, который занимает 4 минуты. После этого он проверяет наличие возможности приземлиться. Если она предоставляется (взлётно-посадочная полоса свободна), то он уходит на посадку, занимая её. Если это не так, то он уходит на четвёртый круг, который занимает 4 минуты. После этого он проверяет наличие возможности приземлиться. Если она предоставляется (взлётно-посадочная полоса свободна), то он уходит на посадку, занимая её. Если это не так, то он уходит на пятый круг, который занимает 4 минуты. После этого он проверяет наличие возможности приземлиться. Если она предоставляется (взлётно-посадочная полоса свободна), то он уходит на посадку, занимая её. Если это не так, то он уходит на запасной аэродром. Прилёт его туда вызывает увеличение счётчика прибывших самолётов. А после посадки самолёта происходит увеличение счётчика прибывших самолётов.

Во втором сегменте модели представляется поведение самолётов, выруливающих на взлёт. Они представляются транзактами, генерируемыми в соответствии с заданным законом распределения. При этом они имеют более высокий (по сравнению с транзактами, соответствующими самолётам) приоритет, равный 1. Возникший транзакт проверяет то, является ли свободной взлётно-посадочная полоса. Если это так, то он взлетает, занимая её. Даже если в это же время появляется приземляющийся самолёт, то взлетающий, благодаря более высокому приоритету, занимает взлётно-посадочную полосу. После взлёта увеличивается на 1 счётчик улетевших самолётов.

---

В обоих описанных сегментах модели взлётно-посадочная полоса представлена одним и тем же прибором, что позволяет согласовать поведение прилетающих и улетающих самолётов.

Третий сегмент предназначен для генерации транзакта через 1440 минут после начала моделирования с тем, чтобы его прекратить и получить отчёт.

Исходный текст программной модели следующий:

GENERATE 5,2,,,0 ;прилет самолета

TRANSFER BOTH,POSAD,KRUG1 ;проверка незанятости полосы или уход на 1й круг

KRUG1 ADVANCE 4

TRANSFER BOTH,POSAD,KRUG2 ;проверка незанятости полосы или уход на 2й круг

KRUG2 ADVANCE 4

TRANSFER BOTH,POSAD,KRUG3 ;проверка незанятости полосы или уход на 3й круг

KRUG3 ADVANCE 4

TRANSFER BOTH,POSAD,KRUG4 ;проверка незанятости полосы или уход на 4й круг

KRUG4 ADVANCE 4

TRANSFER BOTH,POSAD,KRUG5 ;проверка незанятости полосы или уход на 5й круг

KRUG5 ADVANCE 4

TRANSFER BOTH,POSAD,ZAPAER ;проверка незанятости полосы или уход на зап. аэродр.

POSAD SEIZE POLOSA ;посадка самолёта

ADVANCE 2

RELEASE POLOSA

SAVEVALUE 1+,1 ;совершил посадку, подсчет их числа

TERMINATE

GENERATE 10,2,,,1 ;выруливание на взлет

SEIZE POLOSA ;отлет самолета

ADVANCE 2

RELEASE POLOSA

SAVEVALUE 2+,1 ;взлетел, подсчет их числа

TERMINATE

ZAPAER SAVEVALUE 3+,1 ;уход на зап.аэродр. и подсчет их числа

TERMINATE

GENERATE 1440

TERMINATE 1

START 1

Адекватность построенной модели вытекает из соответствия блоков модели описанию процессов, происходящих в исследуемой системе.

Эксперимент заключается в запуске модели и получении результатом моделирования. Этого достаточно, поскольку за время проведения эксперимента (1440 минут) должно прибыть ориентировочно 288 и убыть 144 самолёта (всего 432 наблюдения). Такое большое число достаточно для подведения достоверных статистических итогов.

Входные параметры модели представляют собой только значения параметров распределения случайных величин, определяющих функционирование системы. Они являются неизменными.

Результаты проведенных экспериментов в виде распечатки файла стандартного отчета системы GPSS представлен ниже.

GPSS World Simulation Report - Untitled Model 1.2.1

Sunday, September 11, 2016 23:37:54

START TIME END TIME BLOCKS FACILITIES STORAGES

0.000 1440.000 27 1 0

NAME VALUE

KRUG1 3.000

KRUG2 5.000

KRUG3 7.000

KRUG4 9.000

KRUG5 11.000

POLOSA 10000.000

POSAD 13.000

ZAPAER 24.000

LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY

1 GENERATE 286 0 0

2 TRANSFER 286 0 0

KRUG1 3 ADVANCE 111 0 0

4 TRANSFER 111 0 0

KRUG2 5 ADVANCE 60 1 0

6 TRANSFER 59 0 0

KRUG3 7 ADVANCE 36 0 0

8 TRANSFER 36 0 0

KRUG4 9 ADVANCE 13 0 0

10 TRANSFER 13 0 0

KRUG5 11 ADVANCE 9 1 0

12 TRANSFER 8 0 0

POSAD 13 SEIZE 278 0 0

14 ADVANCE 278 0 0

15 RELEASE 278 0 0

16 SAVEVALUE 278 0 0

17 TERMINATE 278 0 0

18 GENERATE 144 0 0

19 SEIZE 144 0 0

---