Файл: Тема Центр масс. Теорема о движении центра масс. Теорема о движении центра масс неинерциальные системы отсчета. Силы инерции. Физический смысл массы. Применение законов сохранения. Движениетела переменной массы. План.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 84
Скачиваний: 61
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема: Центр масс. Теорема о движении центра масс.Теорема о движении центра масс неинерциальные системы отсчета. Силы инерции.Физический смысл массы. Применение законов сохранения. Движениетела переменной массы.
План:
-
Центр масс. Движение центра масс: -
Теорема о движении центра масс. -
Теорема о движении центра масс неинерциальные системы отсчета. -
Силы инерции. -
Физический смысл массы. -
Применение законов сохранения. -
Движениетела переменной массы.
Введение
Допустим, что у нас есть некоторая система, состоящая из n n-ного количества материальных точек. Возьмем одну из них и обозначим ее массу как m k mk. Приложенные к точке внешние силы (как активные силы, так и реакции связей) имеют равнодействующую F k e Fke. Внутренние силы имеют равнодействующую F k l Fkl. Наша система находится в движении, следовательно, нужная точка будет иметь ускорение a k ak. Зная основной закон динамики, мы можем записать следующую формулу: m k a k = F k e + F k l mkak=Fke+Fkl. Ее можно применить к любой точке системы. Если мы спроецируем эти равенства на соответствующие координатные оси, то у нас получатся дифференциальные уравнения движения в проекциях. Но в конкретных задачах чаще всего вычислять движение каждой точки системы не требуется: можно ограничиться характеристиками движения всей системы в целом. Движение центра масс: основная теорема Характер движения системы можно определить, зная закон, по которому движется ее центр масс. Определение 1 Центр инерции системы (центр масс) – это воображаемая точка с радиус-вектором R R, выражаемым через радиус-векторы r 1 , r 2 , . . . r1, r2, ... соответствующих материальных точек по формуле R = m 1 r 1 + m 2 r 2 + . . . + m n r n m R=m1r1+m2r2+...+mnrnm. Здесь сумма показателей в числителе m = m 1 + m 2 + . . . + m 3 m=m1+m2+...+m3 выражает общую массу всей системы. Для нахождения этого закона нам нужно взять уравнения движения системы, приведенные в предыдущем пункте, и сложить их правые и левые части. У нас получится, что: ∑ m k ¯¯¯¯ a k = ∑ ¯¯¯¯ F k e + ∑ ¯¯¯¯ F k l ∑mkak¯=∑Fk¯e+∑Fk¯l. Взяв формулу радиус-вектора центра масс, получим следующее: ∑ m k r k = M r c ∑mkrk=Mrc. Теперь возьмем вторую производную по времени: ∑ m k a k = M a c ∑mkak=Mac. Здесь буквой ¯¯¯ a c ac¯ обозначено ускорение, которое приобретает центр масс системы. Определение 2 Свойство внутренних сил в системе гласит, что F k l Fkl равно нулю, значит, окончательное равенство будет выглядеть так: M ¯¯¯ a c = ∑ ¯¯¯¯ F k e Mac¯=∑Fk¯e. Это уравнение является записью закона движения центра масс. Запишем его: Движение центра масс системы идентично движению материальной точки той же массы, что и вся система целиком, к которой приложены все действующие на систему внешние силы. Иначе говоря, произведение ускорения центра масс системы на массу самой системы будет равно геометрической сумме всех внешних сил, действующих на эту систему. Нужна помощь преподавателя? Эти равенства являются дифференциальными уравнениями движения центра масс в проекции на оси в декартовой системе координат. Практическое значение теоремы о движении центра масс Данная теорема имеет большую практическую ценность. Поясним, в чем именно она заключается. Теорема 1 Любое тело, движущееся поступательно, может быть рассмотрено в качестве материальной точки, масса которой равна массе всего тела. Во всех других случаях такой подход возможен лишь тогда, когда для определения положения тела в пространстве нам будет достаточно знать, в каком положении находится его центр масс. Также важно, чтобы условия задачи допускали исключение вращательной части движения тела. С помощью теоремы движения центра масс системы мы можем не рассматривать в задачах неизвестные нам заранее внутренние силы. Разберем пример применения теоремы для решения практической задачи. Пример 1 Условие: к оси центробежной машины на нити подвешено кольцо из металла. Оно совершает равномерные вращательные движения с угловой скоростью, равной ω ω. Вычислите, на каком расстоянии центр кольца находится от оси вращения.
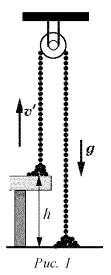
Задача 1. Однородная неупругая цепь длиной L и массой М перекинута через блок. Часть цепи лежит на столе высотой h, а часть на полу. Найти скорость равномерного движения звеньев цепи (рис. 1).
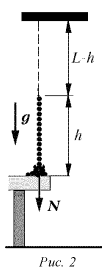
Задача 2. Однородная нерастяжимая цепь подвешена на нити так, что нижний конец ее касается крышки стола. Нить пережигают. Найти силу давления цепочки на стол в тот момент, когда над ним находится часть цепи длиной h. Масса цепи – М, ее длина – L, удар каждого звена считать абсолютно неупругим (рис. 2).
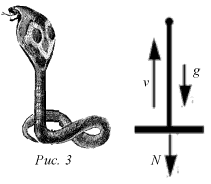
Задача 3. С какой силой давит на землю кобра, когда она, готовясь к прыжку, поднимается вертикально вверх с постоянной скоростью v (рис. 3)? Масса змеи – M, ее длина – L.
 |  |  |
Начнем с хорошо известной ситуации. Пусть тело можно считать материальной точкой (например, можно пренебречь его структурой и размерами или вести речь только о центре масс тела) либо все части протяженного тела имеют одну и ту же скорость v. Тогда 2-й закон Ньютона, в теоретической механике чаще говорят – уравнения движения, для такого тела имеет вид:
где m – неизменная масса тела, F – действующая на тело внешняя сила. В общем случае протяженных тел отдельные части тела движутся каждая со своей скоростью, и описание движения всех частей с учетом их взаимодействия резко усложняется.
Однако бывают случаи, когда движение некоторых частей составного тела можно описать сравнительно просто. Одним из таких случаев является случай движения тел переменной массы. Пусть имеется составная система и пусть в ней можно выделить некоторую часть, подсистему, движущуюся со скоростью v, причем состав ее меняется определенным образом. Будем называть эту подсистему телом переменной массы, если выполнены следующие условия. В каждый момент времени можно считать, что это тело либо является материальной точкой, либо все его части имеют одинаковую скорость v. С течением времени от тела непрерывно отделяются некоторые (бесконечно) малые его части, причем каждая со своей независимой скоростью v'; либо, наоборот, к телу непрерывно добавляются новые малые части, которые до «прилипания» имели свою скорость v' (возможно и то и другое). Таким образом, при движении тела меняется не только его скорость v = v(t), но и масса m = m(t), причем известна скорость изменения массы
Случай <0 означает, что за промежуток времени t t + dt от тела отделяются какие-то части массой –dm; случай Случай >0 означает, что за тот же промежуток времени к телу добавляются какие-то части массой dm. Примером первого случая являются ракета и поливальная машина, примером второго случая – снежная лавина. Мы ограничимся ситуациями, когда все отделяющиеся или добавляющиеся части имеют в каждый момент времени одну и ту же скорость v' = v'(t), следовательно, одну и ту же скорость u = v' – v относительно тела. Эту скорость u = u(t) называют относительной скоростью. Если она известна наряду с (например, в случае ракеты она определяется приготовлением, в случае снежной лавины v' = 0, стало быть, u = –v), то говорят о движении тела переменной массы.2-й закон Ньютона для тел переменной массы имеет вид:
где F – суммарная внешняя сила, которая действует в данный момент времени как на тело (переменной массы m), так и на его отделяющиеся или добавляющиеся части (массы –dm или dm соответственно). Эту тонкость надо постоянно иметь в виду. Может случиться, что вся внешняя сила или конечная ее составляющая приложена именно к этим частям: под действием конечной внешней силы (бесконечно) малая масса (–dm или dm) за (бесконечно) малый промежуток времени t t + dt меняет свою скорость на конечную величину, от v до v' или от v' до v, испытывая (бесконечно) большое ускорение. Именно этот случай реализуется в приводимых ниже задачах. Конечно, может случиться, что изменение скорости отделяющихся или добавляющихся частей обеспечивается внутренними силами. Так обстоит дело, например, в случае космической ракеты или снежной лавины.
2-й закон Ньютона для тел переменной массы можно переписать в эквивалентной форме (особенно удобной во втором случае):
Отличие от привычного случая постоянной массы состоит в том, что m = m(t) является теперь известной функцией времени, а к внешней силе F добавляется реактивная сила
Дадим вывод 2-го закона Ньютона для тел переменной массы (при первом чтении этот абзац можно пропустить). Он следует из 2-го закона Ньютона для любой, в том числе составной системы, в следующей общей форме:
т.е. приращение dp полного импульса p системы за интервал времени t t + dt равно импульсу Fdt действующей на систему внешней силы F. Системой в рассматриваемом интервале времени t t + dt является тело переменной массы вместе с отделяющимися или добавляющимися частями. В любом случае (
>0 или <0 ) изменение dp импульса p за промежуток времени t t + dt дается формулой:dp = p(t + dt) – p(t) = (m + dm)(v + dv) – dmv' – mv.
Вывод этой формулы предоставляем читателю в качестве упражнения. Укажем лишь, что первое слагаемое справа относится ко времени t + dt, третье слагаемое – ко времени t, а второе слагаемое (–dmv') относится к моменту t + dt в случае отделяющихся частей (массой –dm > 0,
<0 ) и к моменту t в случае добавляющихся частей (массой dm, >0 ). Раскрывая правую частьdp = mdv – dm (v' – v) + dmdv = mdv – dmu + dmdv
и приравнивая ее Fdt, имеем:
Деля обе части последнего равенства на dt, переходя к переделу dt 0 и отбрасывая стремящееся к нулю слагаемое
получаем окончательно:
Из вывода следует указанное выше содержание понятия внешней силы F.
Теперь перейдем к решению задач.
Задача 1.Возьмем в качестве тела переменной массы лежащий на столе участок цепи. Цепь считается нерастяжимой
, толщина цепи – пренебрежимо малой, поэтому можно считать, что весь этот участок занимает пренебрежимо малый объем (сосредоточен в точке) в основании левого вертикального участка цепи. Движение носит одномерный характер, вдоль вертикальной оси y (начало отсчета на полу), поэтому достаточно рассматривать только y-компоненту 2-го закона Ньютона (значок «y» для у-компонент векторов v, u, F в дальнейшем опускаем):
(прочие компоненты уравнений движения имеют вид 0 = 0). Именно это уравнение должно определить скорость равномерного движения вертикальных звеньев цепи, поскольку они отделяются от нашего тела.
В каждый момент времени все звенья рассматриваемого участка свободно, без натяжения, лежат на столе, v = 0, соответственно
, сила тяжести компенсируется силой реакции стола. Отделяющееся первое сверху звено, лежащее в основании вертикального участка, уходит вверх с постоянной во времени вертикальной скоростью v' > 0. Эта скорость и является искомой. Относительная скорость u = v' – v = v'. Масса тела m = l, где l – длина рассматриваемого участка, 
– линейная плотность цепи. Длина l, а значит, и масса m, уменьшаются за счет уходящих вверх звеньев; вследствие нерастяжимости цепи 
соответственно
Остается определить вертикальную компоненту F внешней силы F. Она равна натяжению Th левой вертикальной части цепи на нижнем ее конце, находящемся на высоте y = h. Приложена эта сила к отделяющемуся от тела первому сверху звену, тогда как все звенья тела лежат свободно (см. выше о внешней силе F). Th в свою очередь определяется условиями движения вертикальных участков цепи. Если они движутся равномерно, как это и принимается в условии задачи, и, кроме того, цепь справа ложится на пол свободно, т.е. натяжение T0 правого вертикального участка на нижнем его конце, у пола, на высоте y = 0, равно нулю (T0 = 0), то Th равно разности веса Pправ правого участка и веса Pлев левого вертикального участков цепи: Th = Pправ – Pлев.