Жылдамдықтары белгілі, мысалы, ₁ және ₂ жылдамдықтардың аралығында жататын молекулалардың саны туралы айтуға болады. Жылдамдықтар бойынша таралып бөлінуі туралы заңды бірінші рет Дж. Максвелл қорытып шығарды. Максвелл ықтималдық теориясын пайдаланып, мен + жылдамдықтарының арасына жататын молекулалардың dN санын есептеп шығарған

, (8.2)

. (8.3)

Осылайша анықталған функциясы газ молекулаларының жылдамдықтар бойынша бөлінуін сипаттайды да бөліну функциясы деп аталады. Оның мәні мынада: функциясы жылдамдықтары жылдамдықтың берілген мәнінен бірлік интервалда жататын молекулалардың үлесін анықтайды. функциясы нормалау шартын 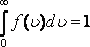қанағаттандырады.

Максвелдің бөліну функциясы 8.1 Суретінде көрсетілген және келесі формуламен өрнектеледі

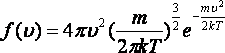. (8.4)

8.4 формуласынан көретініміз, бұл функцияның түрі газдың тегіне (молекула массасына ) және күй параметріне (Т температурадан) тәуелді екенін көреміз.

Кез келген таңдап алынған молекуланың жылдамдығының интервалында жату ықтималдылығы тең.

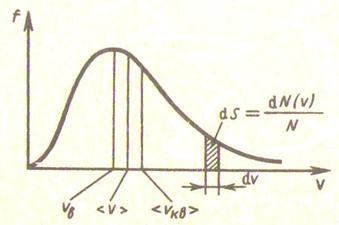
8.1 Сурет

Максвелл таралуының негізгі қасиеттері:

 молекулалардың өте аз үлесі ғана өте кіші және өте үлкен жылдамдықтарға ие болады;

 функциясының максимумына сәйкес келетін ықтималдық жылдамдық болады, сондықтан молекулалардың едәуір бөлігі жылдамдыққа жақын жылдамдықпен қозғалады

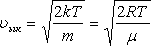; (8.5 )

 таралу қисығының симметриялы болмауына байланысты жылдамдығы -тан жоғары молекулалардың үлесі жылдамдықтағы молекулалар үлесіне қарағанда әрдайым жоғары болады. Бұл диспропорция температура артқан сайын күшейеді ( функциясы графигінде және -ге арналған қисықтар).

 таралу функциясын біле отырып, жылдамдыққа тәуелді кез келген физикалық шаманың орташа мәнін анықтауға болады.

Орташа арифметикалық жылдамдық

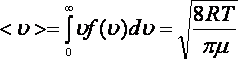. (8.6)

Орташа квадраттық жылдамдық

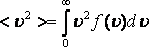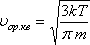; ; . (8.7)

таралуы бөлшектердің бір-бірімен өзара қалай әсерлескеніне тәуелсіз. Ол тепе-теңдік күйдің орнығу процесінде бөлшектердің энергиямен алмасу қабілетімен анықталады.

Максвелл заңында қисықтың түрі температураға байланысты болады. Жүйенің температурасы жайлы жылдамдықтары Максвелл заңы бойынша таралатын жүйедегі бөлшектердің жылулық (хаосты) қозғалысы орныққан жағдайда айтуға болады.

8.2 Сыртқы потенциалды өрістегі бөлшек үшін Больцман бөлінуі

Жылулық қозғалыс кезінде бөлшектің қозғалыс бағыттары тең ықтималды, ал әр бөлшектің орнында болатын өзгерістер кездейсоқ сипатқа ие. Сондықтан бөлшектің сол немесе басқа орында болу ықтималдылығы жөнінде айтуға тура келеді.

Идеал газ V көлемді алып тұр және T температурада тепе-теңдік күйде тұр деп айтайық. Сыртқы өріс жоқ кезде кез келген молекуланың орналасуы тең ықтималды. Сондықтан газ барлық көлемде бірдей концентрациямен таралады.

Егер газ сыртқы күш өрісінде орналасқан болса, газ бөлшектері осы өрістің әсеріне ұшырайды. Газдың тығыздығы мен қысымы әр жерде әртүрлі мәнге ие болады. Сыртқы күш өрісі потенциалды және тек бір z бағытында ғана әсер ететін жағдайды қарастырайық. Бөлшектің потенциалдық энергиясын деп белгілейік. Жылулық тепе-теңдік жағдайында сыртқы күш өрісінің әсеріне түскен газ бөлшектерінің концентрациясы

---

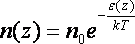(8.8)

заңы бойынша өзгереді. Бұл қатынас Больцман заңы деп аталады. Жердің тартылыс өрісін қарастырайық. Жер бетіне жақын жерде молекуланың потенциалдық энергиясы . екенін ескерсек, жер бетінен z биіктіктегі газдың қысымының өрнегін аламыз:

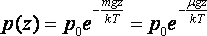. (8.9)

Бұл өрнек барометрлік формула деп аталады. Оны едәуір сиретілген газдар қоспасы (ауа) үшін де қолдануға болады.

Бұл екі қарастырылған таралуларды Максвелл-Больцман заңы деп біріктіріп қарастыруға да болады. Нақты газдар үшін ол тек бір-бірінен алыс қашықтықтағы молекулалар арасында өзара әсерлесуді ескермеген кезде ғана қолданылады. Өте төмен температураларда (азғындалған газдар аймағы) молекулалардың қозғалысы классикалық заңдарға бағынбайды.

8.4 Энергияның еркіндік дәрежелері бойынша біркелкі бөліну заңы. Еркіндік дәрежелері

Молекуланың орташа энергиясы

(8.10)

молекуланың тек ілгерілемелі қозғалысының энергиясын ғана көрсетеді. Алайда молекулалардың ілгерілемелі қозғалысымен қатар, молекулалардың айналуы және молекуланың қозғалыс құрамына кіретін атомдардың тербелуі де мүмкін. Қозғалыстың бұл екі түрі қандай да бір энергия қорымен байланысты болады, ал бұл энергияны анықтауға статистикалық физика тағайындайтын энергияның молекуланың еркіндік дәрежелері бойынша біркелкі таралуы жөніндегі қағида мүмкіндік береді.

Еркіндік дәрежесі бойынша энергияның біркелкі таралу заңы - классикалық жүйелерге қолданатын статистиканың негізгі заңдарының бірі. Механикалық жүйенің еркіндік дәрежелері саны деп жүйенің орнын анықтауда мүмкіндік беретін тәуелсіз координаталардың жиынтығын айтады. Материалдық нүктенің кеңістіктегі орны оның үш координаттарының мәндерімен анықталады. Газдардың жылу сыйымдылығын өлшегенде атомдарды материалдық нүктелер деп есептеуге болады. Олай болса, бір атомды молекулалар үш ілгерілемелі еркіндік дәрежеге, екі атомды молекулалар – үш ілгерілемелі, және екі айналмалы, көп атомды молекулалар және абсолютті қатты дене – үш ілгерілемелі және үш айналмалы еркіндік дәрежесіне ие болады. Жылулық тепе-теңдік жағдайында молекуланың әр еркіндік дәрежесіне тең орташа бірдей кинетикалық энергиядан келеді. Мұндағы, - Больцман тұрақтысы. Екі немесе көп атомды молекулалар айналмалы және тербелмелі қозғалыстар жасайды. Тербелмелі қозғалыстың болуы кинетикалық энергияның потенциалдық энергияға ауысуынан және керісінше болуымен байланысты. Молекуладағы атомның тербеліс энергиясын ескерсек, орташа кинетикалық және орташа потенциалдық энергиясын қарастыруымыз қажет. Молекуланың толық энергиясы

, (8.11)

мұндағы i – ілгерілемелі, айналмалы және екі еселенген тербелмелі еркіндік дәрежелері сандарының қосындысы:

. (8.12)

Атомдардың арасында қатаң байланысы бар молекула үшін i молекуланың еркіндік дәрежелерінің санына тең болады.

---

8.5 Идеал газ молекулаларының жылулық қозғалысының орташа кинетикалық энергиясы. Ішкі энергия

Идеал газ молекулалары қашықтықтан әрекеттеспейтін болғандықтан, мұндай газдың ішкі энергиясы жеке молекулалардың энергияларының қосындысынан тұрады. Демек, идеал газдың бір киломолінің ішкі энергиясы Авагадро санын бір молекуланың орташа энергиясына көбейткенге тең болады:

. (8.13)

Массасы m газдың ішкі энергиясы газдың бір молінің энергиясын m массадағы киломольдердің санына көбейткенге тең болады:

. (8.14)

Сонымен (8.14) өрнектен берілген газдың массасы үшін ішкі энергия газ молекуласының еркіндік дәреже көрсеткіші өзгермейтін болса, оның абсолют температурасына тура пропорционал екендігі көрінеді.

8.6 Идеал газдың жылу сыйымдылығының молекула-кинетикалық теориясы және оның шектелуі

Қандай да бір дененің жылу сыйымдылығы деп оның температурасын бір градусқа көтеру үшін керекті жылу мөлшеріне тең шаманы айтады. Егер де денеге берілген dQ жылу мөлшері оның температурасын dТ шамасына арттыратын болса, анықтама бойынша жылу сыйымдылық

. (8.15) болады. (8.15) шамасының өлшем бірлігі Дж/K. Заттың бірлік массасының жылу сыйымдылығы меншікті жылу сыйымдылық деп аталады. Оны біз с әрпімен белгілейтін боламыз және өлшем бірлігі Дж/К· кг .

. (8.16)

Заттың киломолінің жылу сыйымдылығын с әрпімен белгілейміз. с-нің өлшем бірлігі Дж/К·моль.

, (8.17)

мұндағы - зат мөлшері.

Заттың киломолінің жылу сыйымдылығы мен осы заттың меншікті сыйымдылығының арасындағы байланыс:

. (8.18)

Жылу сыйымдылығының шамасы денені қыздыру шарттарына тәуелді болады. Қыздыруды көлем немесе қысым тұрақты болған жағдайда жүргізгендегі жылу сыйымдылықтың айрықша маңызы бар. Бірінші жағдайда жылу сыйымдылық- тұрақты көлем кезіндегі жылу сыйымдылық , екінші жағдайда- тұрақты қысым кезіндегі жылу сыйымдылық деп аталады.

Егер қыздыру тұрақты көлем кезінде болатын болса, онда дене сыртқы денелерге қарсы жұмыс жасамайды, сондықтан термодинамиканың бірінші бастамасы бойынша барлық жылу дененің ішкі энергиясын арттыруға жұмсалады:

. (8.19)

Демек, тұрақты көлемде идеал газдың киломолінің жылу сыйымдылығын алу үшін газдың ішкі энергиясының (8.13) өрнегін температура бойынша дифференциалдап, былай жазамыз:

. (8.20)

Осы өрнектен көріп отырғанымыздай, тұрақты көлемде идеал газдың жылу сыйымдылығы газ күйінің параметрлеріне, олардың ішінде температураға, тәуелсіз тұрақты шама болып шықты.

Егер газды қыздыру тұрақты қысымда өтетін болса, онда газ ұлғаяды да сыртқы денелерге оң жұмыс жасайды. Демек, бұл жағдайда газдың температурасын бір градусқа арттыруға тұрақты көлем кезіндегіге қарағанда жылу көбірек керек болады, өйткені жылудың бір бөлігі газдың істейтін жұмысына кетеді. Сондықтан, тұрақты қысымдағы жылу сыйымдылық тұрақты көлемдегі жылу сыйымдылықтан артық болуы керек.

---

Бір киломоль газдың тұрақты қысымдағы жылу сыйымдылығы:

, (8.21)

қосылғышы, жоғарыда көргеніміздей, киломоль газдың тұрақты көлем кезіндегі жылу сыйымдылығын береді. Сондықтан (8.21) формуласын мына түрде жазуға болады:

, (8.22)

шамасы, р тұрақты болып, температура бір градусқа артқан кездегі киломоль көлемінің өсімшесі болып табылады. күй теңдеуінен . Осы өрнекті Т (р=const) бойынша дифференциалдап, мынаны аламыз: осы нәтижені (8.22)-ге қойып, мынаны аламыз:

. (8.23)

Сонымен, идеал газдың киломолінің тұрақты қысымда бір градусқа арттырған кезде оның жасайтын жұмысы газдың универсал тұрақтысына тең екен.

(8.22) формуласын ескеріп, үшін мынадай өрнек аламыз:

. (8.24)

(8.24)-ті (8.20)-ге бөліп, әрбір газға тән -нің -ге қатынасын табамыз:

. (8.25)

Бұл өрнектен байқағанымыздай, шамасы молекуланың еркіндік дәрежесінің саны мен сипаты арқылы анықталады.

9 дәріс. Термодинамика негіздері

Дәрістің мақсаттары:

 термодинамиканың заңдарын (бастамаларын) оқып үйрену ;

 макрожүйеде өтетін процестерді талдауда оларды қолдану әдістерін меңгеру.

9.1 Қайтымды және қайтымсыз жылу процестері

Денелер жүйесі немесе жай жүйе деп біз қарастырып отырған денелердің жиынтығын айтамыз. Кез келген жүйе температура, қысым, көлем және т.с.с. мәндері арқылы айырылатын әр түрлі күйде бола алады. Жүйенің күйін сипаттайтын осындай шамалар күй параметрлері деп аталады.

Жүйенің тепе-тең күйі деп жүйенің барлық параметрлері, сыртқы жағдайлар өзгермей қалған кезде жеткілікті уақыт бойы тұрақты болып қалатын белгілі мәндерін сақтайтын күйін айтамыз. Тепе-тең күйлердің үздіксіз тізбегінен құралған процесс тепе-тең процесс деп аталады. Тепе-тең күй ұғымы мен қайтымды процесс ұғымы термодинамикада үлкен рөл атқарады.

Қайтымды процесс деп, кері бағытта өткізуге болатын процесті тура бағытта өткізгенде жүйе қандай күйлерден өтсе, кері бағыттағы сондай күйлер тізбегінен өтетін процесті айтады. Қайтымды процеске тек тепе-тең процесс жатады.

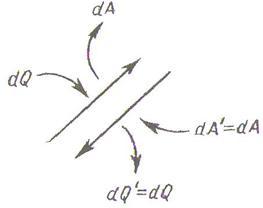
9.1 Сурет

Қайтымды процестің қасиеті мынадай болуы тиіс: егер жүйе тура бағыттағы процестің бір элементар учаскесінде жылу алып, жұмыс өндірсе (9.1 суретті қара), онда кері бағыттағы процестің сондай учаскесінде жүйе жылу береді де, оған жұмыс орындалады. Сол себептен қайтымды процесс әуелі бір бағытта, сонан соң кері бағытта өткеннен кейін және жүйенің алғашқы күйіне қайтқаннан кейін жүйені қоршаған денелерде ешқандай өзгеріс қалмауы тиіс.

Тепе-тең емес процестер әрқашан да қайтымсыз процес, дәлдеп айтқанда нақты процестер қайтымсыз процестер болады. Олар мейлінше баяу өте отырып, қайтымды процестерге тек жуықтай алады.

Дөңгелек процесс (яғни, цикл) деп, жүйе бірсыпыра өзгерістерге ұшырағаннан кейін алғашқы күйіне қайтып келетін процесті айтады. Графикте мұндай цикл тұйық қисық сызықпен кескінделеді (9.2 суретті қара).

---

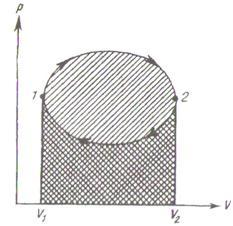
9.2 Сурет

Дөңгелек процесс кезінде орындалатын жұмыс сан жағынан қисықпен қоршалған ауданға тең болады. 1-2 учаскесіндегі жұмыс оң және сан жағынан алғанда, оң жаққа көлбей штрихталған ауданға тең (сағат тілі бағытында орындалатын цикл қарастырылып отыр). 2-1 учаскесіндегі жұмыс теріс және сан жағынан солға қарай көлбей штрихталған ауданға тең. Демек, тұтас цикл ішіндегі жұмыс сан жағынан қисықпен қоршалған ауданға тең болады да, тура бағыттағы циклде (яғни сағат тілі бағытында орындалатын циклде) оң, ал оған кері бағытта теріс болады.

Циклді орындағанан кейін жүйе алғашқы күйіне қайта келеді. Сондықтан күйдің кез келген функциясының, атап айтқанда, ішкі энергияның мәндері циклдің басында және соңында бірдей болады.

9.2 Жылу машиналары және олардың ПӘК-і. Карно циклі. Карно теоремасы

Жылу машиналары деп жүйенің ішкі энергиясының бір бөлігін механикалық энергияға айналдыратын және соның есебінен жұмыс істейтін құрылғыларды айтады.

Барлық жылу машиналарында отынның энергиясы, алдымен жоғарғы температураға дейін қыздырылған газдың немесе будың ішкі энергиясына өтеді. Ұлғаю барысында газ сыртқы күштерге қарсы жұмыс атқарады және салқындайды, яғни оның ішкі энергиясы азаяды. Бұл газдың ішкі энергиясының бір бөлігінің механикалық жұмысқа айналғанын білдіреді. Газдың ішкі энергиясының механикалық энергияға айналмай қалған бөлігі, салқындатқыш рөлін атқаратын тоңазытқыш деп аталатын сыртқы ортаға беріледі. Сонымен, барлық жылу машиналарының құрылымы үш негізгі бөліктен тұрады: отынның энергиясы бөлініп шығатын қыздырғыш; бу немесе газ болып табылатын жұмыс денесі; пайдаланылмай қалған жылу мөлшерін алатын суытқыш. (9.3 суретті қара) жылу машиналары жұмысы жүрісінің сызбанұсқасы келтірілген.

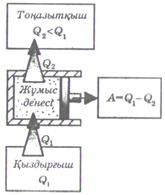
9.3 Сурет

Жұмыс денесі қыздырғыштан жылуды алып, салқындатқышқа жылуды береді және осы жылу мөлшерлерінің айырмасы пайдалы жұмысты береді. Жылу қозғалтқышының тиімділігі оның пайдалы әсер коэффициентімен сипатталады

. (9.1)

(9.1) өрнегі жылу машиналарының ПӘК-і әрқашан бірден кіші болатынын көрсетеді. Бұл қорытынды термодинамиканың бірінші бастамасының салдары болып табылмайды, ол негізгі заңдардың тағы бір түрі – термодинамиканың екінші заңының мазмұнын сипаттап береді. Бұл заңның басқа тұжырымдамалары:

- тек қана жұмыс өндіретін немесе бір жылулық резервуармен энергия алмасуын жасайтын циклдік процесс болуы мұмкін емес (У.Томсон);

 екінші текті мәңгі қозғалтқыш болуы мүмкін емес (В.Оствальд);

- салқын денеден ыстық денеге жылу берілуі мүмкін болатын циклдік процесс болуы мүмкін емес (Р.Клаузиус).

Екінші бастаманың эмпирикалық тұжырымдамалары математикалық түрде тұжырымдалмайды. Олар бір-біріне эквивалентті.

Карно циклі барлық дөңгелек процестердің ішінде ерекше орын алады. Ол бір қыздырғыш пен бір салқындатқыш арқылы арқылы қайтымды түрде орындалатын бірден-бір цикл. Карно циклі екі изотерма және екі адиабатадан тұрады. Жұмыс денесін идеал газ деп алсақ, қайтымды Карно циклі үшін ПӘК-і

---

Смотрите также файлы

• Физика дәріс.docx

• Философия методичка рус.doc

• Философия.docx

• Электротехникалық материалтану зертаханалық жұмыс 3,4.docx

• Электростатика.doc