, (10.8)

мұндағы – молекулалардың тепе-теңдік концентрациясы.

, (10.9)

мұндағы . ( 10.10)

Біз диффузия шамасы үшін өрнекті алдық.

Жылуөткізгіштік жағдайында молекулалардың жылулық қозғалысының орташа энергиясы

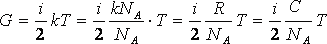. (10.11)

Тасымал теңдеуі мынадай түрге ие болады

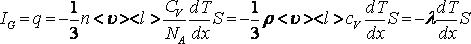, (10.12)

, (10 .13)

мұндағы – жылуөткізгіштік; – тығыздық;

– ортаның изохоралық меншікті жылусыйымдылығы.

Тұтқырлық жағдайында . Сондай-ақ,

, (10.14)

. (10.15)

(10.10), (10.131) және (10.13) теңдеулерінен, , екені шығады.

Тасымал теңдеулеріндегі коэффициенттерінің арасындағы байланыс тасымал құбылыстарының физикалық табиғатының ұқсастығына байланысты және олардың барлығы (10.7) түріндегі бірдей теңдеулермен сипатталады.

11 дәріс. Вакуумдегі электростатикалық өріс

Дәрістің мақсаттары:

- электрстатикалық өрістерді оқып үйрену;

- электрстатикалық өрістерді есептеуге негізгі теоремаларды қолдану.

11.1 Классикалық электрдинамиканың пәні. Электростатиканың негізгі есебі

Электрдинамиканың негізі электр заряды мен электр өрісі болып табылады. Яғни кез келген зарядталған дененің айналасында электр өрісі болады. Зарядталған денелер немесе бөлшектер бір-бірімен осы өріс арқылы әсерлеседі. Электр заряды денелердің электрлік әсерлесуін сипаттайды. Электр зарядтарының қасиеттері:

- электр зарядтары оң және теріс болады, аттас зарядтар бір-бірінен тебіледі, ал әр аттас зарядтар бір-біріне тартылады;

- электр заряды релятивтік - инвариантты: ол қозғалыс кезінде мәнін

өзгертпейді, яғни оның шамасы санақ жүйесіне тәуелсіз;

- электр заряды аддитивті, яғни кез-келген жүйенің заряды жүйені

құрайтын бөлшектердің зарядтарының алгебралық қосындысына тең;

- электр заряды дискретті, яғни кез келген бөлшек е элементар зарядтан тұрады, яғни : q= eN.

Элементар заряды бар бөлшектер электрон ( теріс ) және протон (оң),

Элементар заряд /е/ = 1,6 10^-19 Кл.

Электр зарядының сақталу заңы - тұйықталған жүйенің электр заряды осы жүйеде өтетін кез келген процесс кезінде өзгермейді.

q₁ + q₂ + q₃+ ….+ q_n = const

Нүктелік заряд деген өлшемі мен пішінін ескермеуге болатын электр заряды бар дене.

Электр зарядының сызықтық тығыздығы

(11.1)

мұндағы dq - ұзындығы dl зарядталған сызықтық элементтің заряды.

Электр зарядының беттік тығыздығы

(11.2)

мұндағы dq - зарядталған беттің dS элементар бөлігінің заряды.

Электр зарядының көлемдік тығыздығы

(11.3)

мұндағы dq - зарядталған дененің dV элементар көлемінің тығыздығы

Зарядтардың өзара әсерлесуі Кулон заңымен сипатталады. Ол екі нүктелік зарядталған дененің вакуумдегі өзара әсерлесу күшінің осы денелердің және зарядтарына және олардың ара қашықтығына тәуелділігін тағайындайды. Халықаралық бірліктер жүйесінде заң былай жазылады:

, (11.4)

мұндағы = 8,85*10^-12Кл²/Н*м² - электр тұрақтысы.

Зарядталған бөлшектер мен денелер бір-бірімен өріс арқылы әсерлеседі. Қозғалмайтын электр зарядтарының тудыратын өрісі уақыт бойынша өзгермейді және электрстатикалық өріс деп аталады. Зарядталған бөлшектерге электрстатикалық өріс тарапынан әсер ететін күш электрстатикалық күш деп аталады. Электрстатикада қолданылатын модель өлшемі басқа зарядталған денеге дейінгі қашықтықпен салыстырғанда ескермеуге болатын зарядталған дене - нүктелік заряд.

---

Электрстатикалық өрістің күштік сипаттамасы өрістің кернеулігі болып табылады, ол бірлік оң зарядқа әсер ететін күшпен анықталады:

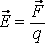, (11.5)

мұндағы - өрістің берілген нүктесіне орналасқан оң зарядқа әсер ететін күш. Кернеулік векторының бағытына өрістің берілген нүктесінде орналасқан бірлік оң зарядқа әсер ететін кулондық күштің бағыты алынады.

Егер кернеулік векторы өрістің барлық нүктелерінде бірдей болса, өріс біртекті өріс деп аталады.

Электрстатикалық өрісті кескіндеу үшін күш сызықтары қолданылады. Күш сызықтары немесе кернеулік сызықтары деп әр нүктесінде жүргізілген жанама сол нүктедегі өріс кернеулігі векторымен бағыттас болатын сызықтарды айтады. Кернеулік сызықтары оң зарядтардан басталып, теріс зарядтарда аяқталады, олар еш жерде қиылыспайды, себебі әрбір нүктедегі кернеуліктің тек бір мәні және белгілі бағыты бар болады.

Кулондық күштерге механикадағы күш әсерлерінің тәуелсіздік принципі қолданылады. Сонымен, өрістің кез келген нүктесіндегі q₀ сыншы зарядқа әсер етуші қорытқы күш оған түсірілген жүйедегі әр бір q _i зарядтардың әсер күштерінің векторлық қосындысына тең

. (11.6)

Берілген зарядтар жүйесіндегі қорытқы өріс кернеулігі үшін осы өрнекті ескеріп, былай жазуға болады:

. (11.7)

Зарядтар жүйесінің өріс кернеулігі жүйені құрайтын зарядтардың кернеуліктерінің қосындысына тең болады. Бұл суперпозиция принципі деп аталады.

Электрстатиканың негізгі есебі - өрістің негізгі сипаттамалары: өріс кернеулігін және потенциалын берілген шамалар бойынша табу және кеңістікте зарядтардың таралуын анықтау. Бұл есепті екі жолмен шешуге болады. Олар: суперпозиция принципі және Гаусс теоремасы.

11.2 Кернеулік Е векторының ағыны. Гаусс теоремасы және оны электростатикалық өріс кернеуліктерін есептеу үшін қолдану

Электр өрісінің бет арқылы өтетін кернеулік векторының ағыны

, (11.8)

мұндағы – кернеулік векторының элементар бетке түсірілген нормаль бағытындағы проекциясы. Бұл шама өрістің конфигурациясына ғана емес, бетке түсірілген нормаль бағытын таңдауына да байланысты. Тұйықталған бет үшін нормальдың оң бағыты ретінде осы бетпен қамтылған сыртқы аймаққа қарай бағыт алынған. Тұйықталған бет арқылы өтетін кернеулік векторының ағыны осы бет ішіндегі зарядтардың алгебралық қосындысына ғана тәуелді:

. (11.9)

Бұл формула вакуумдегі электрстатикалық өріс үшін Гаусс теоремасын өрнектейді. Гаусс теоремасы былай тұжырымдалады: тұйықталған бет арқылы өтетін векторының ағыны осы бетпен қамтылған көлем ішіндегі зарядтардың алгебралық қосындысын электр тұрақтысына бөлгенге тең.

Симметриялы зарядтар жүйесінің электрстатикалық өрісін есептеуде Остроградский-Гаусс теоремасын қолдану ыңғайлы. Ол үшін өріс сипатын анықтап, берілген нүкте арқылы өтетін тұйықталған гаусстық бетті таңдау қажет. Остроградский-Гаусс теоремасын біркелкі зарядталған шексіз сымның, екі параллель шексіз жазықтықтың, зарядталған сфералық және цилиндрлік беттердің электрстатикалық өрістерін есептеуге қолдануға болады.

---

Мысал ретінде көлемдік зарядпен біркелкі зарядталған, радиусы R дөңгелек цилиндрдің өрісін есептейміз. Гаусстық бет ретінде радиусы r және биіктігі болатын, осі берілген цилиндрдің осімен сәйкес келетін дөңгелек цилиндрдің бетін алу ыңғайлы.

. (11.10)

Өрістің аймағы үшін екенін ескеріп алатынымыз

(11.11)

Ал жағдай үшін

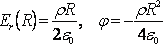. (11.12)

Өрістің аймағында

және

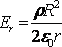. (11.13)

11.3 Электрстатикалық өріс жұмысы. Электрстатикалық өріс кернеулігі векторының циркуляциясы

Қозғалмайтын q зарядтың электрстатикалық өрісінде q₀ нүктелік сыншы заряд 1 нүктеден 2- нүктеге орын ауыстырғанда өріс тарапынан әсер ететін күш жұмысы

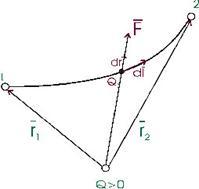
11.1 Сурет

Электрстатикалық өріс жұмысы

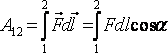, (11.1)

мұндағы_– күш векторымен -орын ауыстыру арасындағы

бұрыш.

Кулон заңы мен қатынасын пайдаланып, келесі өрнекті

аламыз:

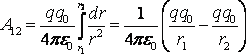. (11.15)

Осы өрнегінен шығатыны, жұмыс орын ауыстыру траекториясына тәуелсіз, тек q₀ зарядының бастапқы 1 және соңғы 2 орындарымен ғана анықталады.

Сондықтан, электрстатикалық өріс - потенциалды өріс, яғни кулон күштерінің зарядты өрістің бір нүктесінен екінші нүктесіне ауыстыру үшін атқаратын жұмысы траектория пішініне тәуелді емес, ол тек нүктенің бастапқы және соңғы орнына ғана байланысты.
Электрстатикалық күш жұмысы:

, , (11.16)

мұндағы - электрстатикалық өрістегі зарядтың потенциалдық энергиясының өзгерісі.

Тұйық жүйеде зарядтың орын ауыстыруына байланысты кулон күші жұмыс атқармайды, яғни А = 0.

Егер сыншы заряд ретінде бірлік оң заряд алатын болсақ, оның орнын 1-орыннан 2-орынға ауыстыру үшін күштің жасайтын жұмысы мынаған тең:

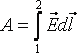(11.17)

Егер электр өрісінің жұмыс тұйықталған траекториямен жасалатын болса, онда жұмыс нөлге тең болады

, (11.18)

- кернеулік векторының циркуляциясы деп аталады. Сонымен, кез келген тұйық контур бойындағы электрстатикалық өрістің кернеулігі векторының циркуляциясы нөлге тең. Бұл электрстатикалық өріс кернеулік сызықтары тұйықталған болуы мүмкін емес екендігін көрсетеді.

Екінші жағынан Гаусс теоремасы электрстатикалық өріс көзі - электр зарядтары екендігін білдіреді.

11.4 Потенциал. Потенциалдың электрстатикалық өріс кернеулігімен байланысы

Электрстатикалық өрістің потенциалы - скаляр шама, өрістің берілген нүктесіндегі бірлік оң нүктелік зарядтың потенциалдық энергиясына тең және өрістің энергетикалық сипаттамасы болып табылады:

. (11.19)

Өріс күшінің потенциалы (1-нүктеден) потенциалы (2-нүктеге) q₀ зарядтың орнын ауыстыруға жасайтын жұмысы

. (11.20)

өрнегімен анықталады.

Нүктелік q зарядтың электрстатикалық өрісінің одан r қашықтықтағы нүктедегі потенциалы:

. (11.21)

Радиусы R, заряды бетінде бірқалыпты таралған шардың электростатикалық өрісінің потенциалы шардан тыс нүктелерде шардың центріне орналастырылған нүктелік q зарядтың өріс потенциалымен бірдей болады. Шардың ішіндегі өріс потенциалы

, (11.22)

---

бірақ шардың ішіндегі өріс кернеулігі нөлге тең.

Электрстатикалық өрісті күш сызықтарымен қатар графиктік түрде эквипотенциалдық беттер арқылы да кескіндейді. Эквипотенциал бет деп барлық нүктелеріндегі потенциалдың мәндері бірдей болып келетін бетті айтады. Эквипотенциалдық беттердің қасиеттері: а) эквипотенциалдық беттің кез келген нүктесінде кернеулік оған перпендикуляр болады және потенциалдың кему жағына бағытталады; б) электр заряды бір эквипотенциалды бет бойымен орын ауыстырғандағы істелінетін жұмыс нөлге тең болады.

Өрістің күштік сипаттамасы кернеулік және оның энергетикалық сипаттамасы – потенциалдың арасында электрстатикалық өрістің потенциалдылығына негізделген байланыс бар. Потенциалды күш өрісінде потенциалдық энергия мен күш арасындағы байланыс мына түрде берілген

, (11.23)

мұндағы –набла операторы, оның түрі:

(11.24)

осыдан

. (11.25)

Мұндағы "минус " таңбасы векторының бағыты әрқашан да потенциалдың кемуіне қарай бағытталатындығын көрсетеді.

11 дәріс. Электрстатикалық өрістегі диэлектриктер

Дәрістің мақсаты:

- диэлектрик ішіндегі электр өрісін оқып үйрену;

- заттардағы электр өрісі үшін Гаусс теоремасын қолдану;

- екі диэлектрик шекарасындағы орын алатын құбылыстар.

12.1 Полярлану. Диэлектрик түрлері

Электрлік қасиеттері бойынша денелер өткізгіштер және диэлектриктер болып бөлінеді.

Диэлектриктер деп электр тогын өткізбейтін заттарды айтады. Диэлектриктерге мысалы, ауа және шыны, эбонит, құрғақ ағаш және қағаз жатады.

Классикалық тұрғыдан қарағанда диэлектриктер өткізгіштерден электр өрісі әсерінен реттелген қозғалыс жасап, электр тогын тудыратын еркін зарядтардың болмауымен ерекшеленеді. Электр өрісіндегі диэлектрикте зарядтар бөлінбейді, яғни онда еркін зарядтар жоқ, атомдарындағы электрондар ядроларымен қатты байланысқан. Бұл байланысты бұзу үшін күшті сыртқы факторлар қажет.

Электрлік диполь – әр аттас екі нүктелік зарядтан тұратын электр жағынан нейтралды жүйе.

Диэлектриктердің молекулалары электр жағынан нейтралды, ол қорытқы заряды нөлге тең жүйе сияқты. Осыған қарамастан молекулалардың электрлік қасиеті бар және ол молекулаларды электрлік диполь ретінде қарастыруға болады.

Мұндай дипольдің оң заряды оң зарядтардың «ауырлық центрінде» орналасқан ядроның қорытқы зарядына тең, ал теріс заряды теріс зарядтардың «ауырлық центрінде» орналасқан электрондардың қорытқы зарядына тең. Осындай дипольдің электрлік моменті ( – молекуладағы барлық атомдық ядролардағы оң зарядтардың қорытқысы, – электрондардың «ауырлық центрінен» атомдық ядролардағы оң зарядтардың «ауырлық центрін» қосатын вектор).

Диэлектриктерді сыртқы электр өрісіне енгізгенде сыртқы өріс әсерінен оларда нөлден өзгеше электр моменті пайда болады, яғни диэлектрик полярланады.

---

Сыртқы электр өрісі әсерінен дипольдердің өріс бағытына сәйкес ығысу құбылысын диэлектриктердің полярлануы деп атайды. Нәтижесінде диэлектриктің қандай да бір көлеміндегі электр моменті нөлден өзгеше болады, яғни заттың бетінде байланысқан зарядтар пайда болады. Осы зарядтар тудыратын электр өрісінің кернеулігі диэлектриктің ішінде сыртқы электр өрісінің кернеулігіне қарсы бағытталады. Сондықтан да диэлектрик ішіндегі электр өрісі әлсірейді. Диэлектриктің ішіндегі өрістің қорытқы кернеулігі:

. (12.1)

Вакуумде электр өрісі кернеулігі модулінің біртекті диэлектриктегі өрістің модуліне қатынасына тең шаманы заттың диэлектрлік өтімділігі деп атайды:

. (12.2)

Бұл физикалық шаманың өлшем бірлігі жоқ, электр өрісінде диэлектриктердің полярлану шамасын сипаттап, өрістің диэлектриктерде қаншалықты әлсірейтіндігін көрсетеді.

Диэлектриктер үш топқа бөлінеді: полярлы, полярлы емес және кристалды.

Полярлы диэлектриктерде оң және теріс зарядтардың таралу нүктелері сәйкес келмейді және электр өрісіне енгізілген кезде бұл диэлектриктердің молекулалары кернеулік векторының бағытына қарай ығысады.

Полярлы емес диэлектриктерде оң және теріс зарядтардың таралу нүктелері сәйкес келеді және электр өрісіне енгізілген кезде бұл диэлектриктердің молекулалары деформацияланып, нәтижесінде дипольдар пайда болады және олар кернеулік векторының бағытына қарай ығысады.

Ионды диэлектриктер (NaCl, KCl) - әртүрлі таңбалы кезектескен иондардан құрылған кеңістікті торды құрайтын кристаллдар.

Диэлектриктердегі полярланудың сандық мөлшері полярлану векторымен сипатталады. Полярлану векторы диэлектриктің шексіз аз көлемінің электрлік диполдік моментінің сол көлемге қатынасымен анықталады

, (12.3)

мұндағы – бір молекуланың дипольдік моменті.

Полярлану векторының модулы диэлектриктердің полярлану дәрежесін анықтайды, ал бағыты полярлану бағытымен сәйкес келеді.

Поляризациялау – полярлануды тудыратын, сыртқы электр өріс кернеулігімен анықталатын макраскопиялық сипаттама.

Изотропты диэлектриктерде полярланудың кез келген түрі сол нүктедегі өріс кернеулігімен мынадай қарапайым байланыста болады (12.4)

мұндағы – диэлектриктің диэлектрлік қабылдағыштығы деп аталатын өлшемсіз шама.

Полярлы емес диэлектриктің аз көлеміндегі барлық молекулалар электр өрісінде бірдей электрлік моменттерге ие болады ( 12.1, а суретті қара), сондықтан полярлану өрнегімен анықталады ( – молекулалардың концентрациясы).

а) б)

1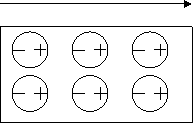 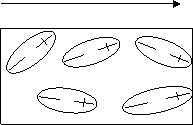2.1 Сурет.

Мұндай диэлектриктердегі диэлектрлік қабылдағыштық температураға тәуелді емес. Температура тек молекулалардың концентрациясына ғана жанама әсері болуы мүмкін.

Полярлы диэлектриктерде сыртқы өрістің ығысуына молекулалардың жылулық қозғалысы кедергі жасайды (12.1, б суретті қара). Нәтижесінде кейбір молекулалардың диполдік моменттері өріс бағытына ығысып, есептеулер мен тәжірибелерден (12.4) өрнегі шығады.

---

Смотрите также файлы

• Физика дәріс.docx

• Философия методичка рус.doc

• Философия.docx

• Электротехникалық материалтану зертаханалық жұмыс 3,4.docx

• Электростатика.doc