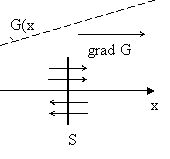Добавлен: 02.02.2019
Просмотров: 13034
Скачиваний: 98
,
.
(9.2)
Карно теоремасы:
қайтымды
Карно циклінің ПӘК-і жұмыстық дененің
табиғатына және осы циклді жасайтын
жүйенің құрылғысына тәуелсіз, ол тек
қыздырғыш
пен
салқындатқыштың
температуралары
арқылы анықталады;
қайтымсыз
машиналардың ПӘК-і (қайтымсыз цикл
бойынша жұмыс істейтін) қайтымды
машиналардың ПӘК-не қарағанда кіші,
яғни
.
Олай болса,
.
(9.3)
Макрожүйелерде нақты қайтымды процестер болуы мүмкін емес, сондықтан (9.2) өрнегі асимптотикалық сипатқа ие, яғни дәл мәнін көрсету мүмкін емес.
Карно теоремасы (9.3) термодинамиканың екінші заңының математикалық өрнегін береді, ол бір қыздырғышы мен бір салқындатқышы бар тұйық процестер үшін ғана қолданылады. (9.3)-гі теңдік белгісі қайтымды процестер үшін, теңсіздік белгісі – қайтымсыз процестер үшін қойылады.
Кез келген цикл жағдайында Карно теоремасының жалпылама түрі Клаузиус теңсіздігін береді (Клаузиус теоремасы)
.
(9.4)
9.3 Энтропия және оның қасиеттері
Термодинамиканың екінші заңының барлық қаралған тұжырымдамалары процестің мүмкіндіктерін талдау үшін энергия мөлшерінің сақталуының жеткіліксіз екенін көрсетеді. Энергия сандық түрде ғана емес, сапалық түрде де сипатталуы қажет. Энергияның сапасын анықтайтын және термодинамиканың екінші заңындағы шектеулерді сандық түрде сипаттайтын шама S энтропия болып табылады.
Термодинамиканың екінші заңының жалпылама тұжырымдамасы энтропия ұғымымен байланысты. Егер жүйе оқшауланған болса, яғни қоршаған ортамен жылу алмаспайтын болса ондай жүйенің энтропиясы:
,
.
(9.5)
Барлық нақты процестердің барлығы қайтымсыз болғандықтан оқшауланған жүйеде энтропия әрдайым артады. Энтропияның артуы жүйенің ықтималдылығы аз күйден ықтималдылығы көп күйге, яғни тепе-теңдік күйге ауысуын көрсетеді.
Бірақ флуктуациялар да болуы мүмкін. Оқшауланған жүйедегі энтропияның арту заңы статистикалық сипатқа ие.
(9.5) –да математикалық түрде өрнектелген термодинамиканың екінші заңы оған дейін қарастырылған тұжырымдамалармен астасады.
Жылу
машиналарының жұмысын талдасақ, жүйеге
dQ
жылу түрінде берілген барлық энергияны
dA
жұмысқа айналдыру үшін оның қандай да
бір бөлігі жеткілікті
,
және неғұрлым аз болса, соғұрлым энтропия
көп болады. Бұл жағдай энтропияны жұмыс
істеу қабілетінің өлшемі деп сипаттауға
мүмкіндік береді. Жүйенің энтропиясының
артуы табиғи процестердің ерекше белгісі
болып табылады және энергия сапасының
төмендеуіне алып келеді.
Кез келген қайтымды цикл үшін Клаузиус теоремасын (9.4) жазайық
.
(9.6)
(9.6)
интегралдың нөлге тең болуы
шамасы
қандай да бір S
күй функциясының
толық дифференциалын береді. Сондықтан
және
.
(9.7)
(9.7) формуласын термодинамикадағы энтропияның анықтамасы ретінде қарастыруға болады.
(9.7) анықтамадан туындайтын энтропияның кейбір қасиеттері:
-
жүйенің энтропиясы - аддитивті шама
Мұның
мәнісі: жүйе энтропиясы оның жеке
бөліктерінің энтропияларының қосындысына
тең;
-
жылу алмасусыз жүретін қайтымды процесте
–
адиабаталық процесте- энтропия тұрақты
болады;
- процестің энтропиясы қандай да бір тұрақты шамаға дейінгі дәлдікпен анықталуы мүмкін.
Қайтымды процестегі энтропияның өзгерісі (9.1) және (9.2) қатынастары негізінде есептеледі
.
( 9.8)
Жылулық процестерді талдау үшін координат осьтері ретінде T және S күй функциялары алынатын TS – диаграммасы қолданылады.
8.5 Термодинамиканың бірінші және екінші бастамасы. Термодинамиканың екінші бастамасының статистикалық түсіндірілуі. Энтропия мен күй ықтималдылығының байланысы
Қандай да бір дененің толық энергиясынан тұтастай қозғалысының кинетикалық энергиясы мен сыртқы күш өрісіндегі потенциалдық энергиясын шығарып тастағанда қалған энергия оның ішкі энергиясы деп аталады.
Демек, ішкі энергия түсінігіне молекулалардың хаосты қозғалысының кинетикалық энергиясы, молекулалардың өзара әсерлесуінің потенциалдық энергиясы және ішкі молекулалық энергия кіреді екен. Ішкі энергия негізінен екі түрлі процестің: дененің А жұмыс істеуі мен денеге берілген Q жылу мөлшерінің есебінен өзгере алады. Жұмыс істеу жүйеге әсер етуші сыртқы денелердің орын ауыстыруымен қоса жүреді.
Денеге жылу беру сыртқы денелердің орын ауыстыруына тәуелді емес. Бұл жағдайдағы ішкі энергияның өзгерісі ыстығырақ дененің жеке молекулаларының салқынырақ дененің молекулаларына қарсы істеген жұмысының әсерінен болады. Бір денеден екінші денеге энергияның берілуіне әкелетін микроскопиялық процестердің жиынтығы жылу берілуі деп аталады.
Жүйе мен қоршаған ортаның арасындағы энергия алмасуының екі тәсілі бар деп тұжырымдалатын термодинамикадағы энергияның сақталу заңы физиканың негізгі заңдарының бірі болып табылады:
Жүйеге берілген жылу мөлшері және жүйеде атқарылған жұмыс жүйенің ішкі энергиясын өзгертуге жұмсалады
,
немесе
,
(9.9)
мұндағы
–
жүйеде атқарылған жұмыс;
–
сыртқы
күштердің атқарған жұмысы.
Ішкі энергия жүйенің күй функциясы болып табылады. Оның өзгерісі тек бастапқы және соңғы күйлеріне байланысты және бір күйден екінші күйге өту тәсіліне тәуелсіз.
Жылу мен жұмыс күйлерге ғана тәуелді болып қалмайды, сондай-ақ процестің түріне байланысты болады; олар процестің функциялары болып табылады.
Термодинамиканың екінші заңы табиғаттағы өтетін процестердің бағытын анықтайды. Екінші бастама бірінші бастама сияқты бірнеше тәсілдермен тұжырымдалуы мүмкін. Ең айқынырақ түрде тұжырымдап айтқанда екінші бастама: жалғыз-ақ нәтижесі жылудың салқын денеден ыстық денеге ауысуы болып келетін процестерді жүзеге асыру мүмкін емес.
Больцманның тағайындауы бойынша, энтропияның қарапайым статистикалық түсініктемесі бар. Егер бір емес, бірқатар күйдің ықтималдылығы бірдей және ең үлкен болса, онда тұйықталған жүйе мұндай күйлердің біреуінен басқаларына көше алады. Сөйтіп, тұйықталған жүйенің энтропиясы мен ықтималдылығының қасиеттері бірдей: олар не арта алады, не өзгеріссіз қала береді.
Келтірілген пайымдаулардан жүйенің энтропиясы мен ықтималдылығының арасында нақтылы байланыс болуға тиіс деген қорытынды шығады. Больцман бұл қатыстың түрі мынандай екенін көрсетті:
,
(9.10)
мұндағы к- Больцман тұрақтысы, ал W- жүйе күйінің термодинамикалық ықтималдылығы, ол шаманы сол күйді жүзеге асыруға болатын түрліше тәсілдердің саны деп түсінуге тиіспіз.
10 дәріс. Теңгерілмеген термодинамикалық жүйелердегі тасымалдану құбылыстары
Дәрістің мақсаттары:
тасымал құбылыстарымен танысу ;
тасымал құбылыстарының ортақ заңдылықтарын, механизмдерін және жеке сипаттамаларын түсіндіру.
10.1 Тасымалдану құбылыстарының жалпы сипаттамалары
Қалыпты жағдайда газдың қысымы мен температурасы қарастырып отырған көлемнің барлық жерінде бірдей болады. Осыған сәйкес қалыпты жағдайда осы көлемде газ молекулалары бірыңғай орналасады, яғни молекулалар саны қарастырылып отырған көлемнің барлық жерінде бірдей болады. Бірақ мұндай орналасу кейбір сыртқы себептерден өзгеріске ұшырайды. Дәлірек айтқанда молекулалардың жылулық қозғалысының және сол қозғалыс кезінде молекулаларды бір жерден екінші жерге көшіріп отырудың салдарынан, олар бастапқы күйіне қайта оралуы мүмкін. Осындай қозғалыстың саладарынан молекулалар бір-бірімен соқтығысып, өздерінің жылдамдықтарының бағыты мен шамасын өзгертеде. Сөйтіп молекулалар үздіксіз бір-бірімен араласып және соның салдарынан газ күйін сипаттайтын параметрлер өзара теңесіп отырады. Мұндай процестерді тасымал құбылыстары деп атайды және бұл құбылыстың нәтижесінде энергияның, массаның, импульстің кеңістіктік тасымалдануы жүреді.
Тасымалдану құбылыстарына: диффузия, жылу өткізгіштік және ішкі үйкеліс құбылыстары жатады.
Берілген көлемде екі түрлі газ немесе молекуланың саны әртүрлі біртекті газ болсын. Олар молекулалардың жылулық қозғалысының әсерінен бір-бірімен араласып, нәтижесінде екі газдағы молекулалар саны теңеседі. Яғни, газ молекулалары ретсіз қозғалып отырады, осыдан барып тиісіп тұрған әр текті екі газ бір-бірімен араласады, яғни диффузияланады. Сөйтіп температура алмасуының әсерінен жылу өткізгіштік құбылысы пайда болады. Ең соңында газдық қабаттар әртүрлі жылдамдықпен қозғалғанда олардың арасында үйкеліс күші пайда болады. Бұл үйкеліс күші газ қабаттарына жанама бағытпен әсер етеді. Сондықтан бұл құбылыс газ қабаттарының ішкі жылдамдықтарының теңесуі болғандықтан, ішкі үйкеліс құбылысы деп аталады.
10.2 Тасымалдану құбылыстарының феноменологиялық теңдеулері
Тасымал құбылыстары жүйені тепе-теңдікке әкелетін процестермен ғана емес, шексіз уақытта жүйені тепе-теңдікте ұстап тұратын сыртқы әсерлерге де байланысты. Мұндай жағдайда олар стационар болып табылады (яғни уақытқа тәуелсіз).
Тасымал процестерінің интенсивтілігі сәйкес шаманың ағынымен сипатталады.
Қандай-да
бір шаманың ағыны деп бірлік уақыт
ішінде қандай-да бір бет арқылы өтетін
осы шаманың мөлшерін айтады (мысалы,
масса ағыны
,
импульс ағыны
және
т.б.).
Ағын – скаляр алгебралық шама, оның таңбасы ағын оң болып саналатын бағытты таңдау арқылы анықталады.
Диффузия деп жылулық қозғалыс салдарынан ортаның тығыздығы жоғары жерінен тығыздығы төмен жерге қарай заттың тасымалдану процесін айтады.
Қандай
да бір ортада
осі
бойынша қандай да бір құраушының
концентрациясы біркелкі таралмайтын
ортаны қарастырайық.
концентрацияның
өзгеру шапшаңдығы
(
– берілген құраушының концентрациясының
градиентінің
осіне
проекциясы) туындысымен сипатталады.
Температура,
қорытқы
концентрация
(тепе-теңдік)
және
қысым барлық жерде бірдей.
Мұндай
кезде молекулалардың
ағыны,
сондай-ақ концентрацияның азаю бағытында
берілген құраушының масса ағыны
пайда
болады.
осіне
перпендикуляр
бет
арқылы өтетін масса ағыны эксперименттік
түрде
,
(10.1)
мұндағы
–
-құраушының
парциал тығыздығы ;
–
берілген
құраушының молекуласының массасы;
–
диффузия
деп аталынатын пропорциналдық коэффициент.
(10.1) теңдеуі Фик заңы деп аталады. Минус таңбасы ағынның орталық берілген құраушысының тығыздығы (концентрациясы) азаю жағына бағытталғанына байланысты қойылады.
Егер
жүйеде температура біркелкі таралмаса
(
),
онда температураның азаю жағына қарай
жылу
ағыны пайда болады
,
(10.2)
мұндағы
–
пропорционалдық коэффициент, ол ортаның
қасиеттеріне тәуелді және жылуөткізгіштік
деп аталады.
(10.3) қатынасы Фурье заңы деп аталады және орта бөлшектерінің хаосты қозғалысынан болатын жылу алмасу процесі – жылуөткізгіштікпен сипатталады.
Егер
газ тәрізді ортада көршілес қабаттардың
жылдамдықтары бірдей болмаса, онда
қабаттан қабатқа (қабат қозғалыстарының
бағытына көлденең) молекулалардың
импульсі тасымалданады.
осіне
перпендикуляр бет арқылы өтетін
импульс
ағыны
.
(10.3)
(10.3)
теңдеуі Ньютон заңы деп аталып, импульс
тасымалы тұтқырлықты немесе ішкі ағынды
сипаттайды. Пропорционалдық коэффициент
болып табылатын
шамасын
ортаның динамикалық тұтқырлығы деп
аталады.
Сонымен, диффузияда ортада қабаттан қабатқа масса, жылу өткізгіштікте – энергия, тұтқырлықта – импульс беріледі. Фик, Фурье және Ньютон заңдары эмпирикалық болып табылады. Олардың теориялық негіздемесін молекулалық физика түсіндіреді.
10.3 Соқтығысулардың орташа саны және еркін жолының орташа ұзындығы
Жылулық
қозғалыстағы газ молекулалары бір –
бірімен үздіксіз қозғалыста болады.
Бірінен соң бірі болатын екі соқтығысу
арасындағы уақытта молекула ι
еркін жүру жолының ұзындығы
деп аталатын қайсыбір жол жүреді. Еркін
жүру жолы кездейсоқ шама. Соқтығысу
кезінде екі молекуланың центрлерінің
арасындағы ең минимал қашықтық молекуланың
эффективтік
диаметрі
деп аталады. Эффективтік диаметр
молекулалардың жылдамдықтары артқан
кезде, яғни температура артқан кезде,
шамалап азаяды.
шамасы
молекуланың эффективтік қимасы деп
аталады.
1 c ішінде молекула орташа есеппен орташажылдамдық < υ > -ге тең жол жүреді. Егер бір секунд ішінде ол z рет соқтығысатын болса, онда молекулалардың еркін жүру жолының орташа ұзындығы
.
(10.4)
Соқтығысулардың
орташа саны z-і есетеп шығару үшін,
қарастырылып отырған молекуладан басқа
молекулалардың барлығы өз орнында
қозғалыссыз қалады деп ұйғаралық.
Қозғалыстағы молекула тыныштықта тұрған
молекуламен соқтығысып, келесі
соқтығысқанға дейін ол түзу сызықты
қозғалыста болады Бір секунд ішінде
молекула < υ >-ға тең жол жүреді. Осы
уақыттың ішінде тыныш тұрған молекулалармен
соқтығысу санының, центрлері ұзындығы
< υ >, радиусы d және көлемі
болатын
сынық цилиндрдің ішінде қалатын
молекулалардың санына тең болатындығы
сөзсіз. Осы көлемді бірлік көлемдегі
молекулалар саны n-ге көбейтіп, қозғалыстағы
молекуланың бір секунд ішінде қозғалмай
тұрған молекулалармен соқтығысуларының
орташа санын аламыз:
.
Қажетті есептеулер көрсеткендей,
молекулалардың салыстырмалы қозғалысының
орташа жылдамдығы молекулалардың
ыдыстың қабырғасына қатысты алынатын
жылдамдығынан екі есе артық болады.
Сондықтан соқтығысулардың бірлік
уақыттағы орташа саны
тең.
Онда молекулалардың еркін жүру жолының
орташа ұзындығы
.
(10.5)
Яғни,
молекулалардың
n концентрациясына кері пропорционал.
10.4 Тасымалдану құбылыстарының газдар үшін молекула-кинетикалық теориясы: жылу өткізгіштік, ішкі үйкеліс, диффузия. Тасымалдану коэффициенттері
Тасымал құбылыстарын сандық түрде талдау үшін молекула қозғалысының кинематикалық сипаттамаларын игеру қажет:
-
молекуланың эффективті диаметрі d
және соқтығысудың эффективті қимасы
;
-
газдың бір молекуласының бірлік уақыт
ішінде алатын орташа соқтығысу саны
;
- молекулалардың орташа еркін жүру жолы
.
(10.6)
шамасы
бір молекуланың молекулалық қасиетін
(бұл энергия, импульс, концентрация,
заряд және т.б. болуы мүмкін) сипаттайды
делік.
|
|
|
|
|
|
10.1 Сурет
Ортада
осы шаманың
осі
бойымен градиенті бар деп есептейміз.
осіне
перпендикуляр
бетті
(10.1 суретті қара) бөліп алып, жылулық
қозғалыс салдарынан осы бет арқылы
өтетін
шамасының
қорытқы
ағынын есептейік.
бетті
тек соқтығысудың соңғы мезетінде беттен
орташа еркін жүру жолынан аспайтын ара
қашықтықта орналасқан молекулалар ғана
қиып өтетінін ескеру керек. Осылайша
осі
бойымен (немесе оған қарама-қарсы)
бағытталған ағынды аламыз:
.
(10.7)
(10.7)
теңдеуі
бет
арқылы өтетін
шамасының
ағынын анықтайтын тасымал құбылыстарының
негізгі теңдеуі болып табылады. (10.7)
теңдеуінен Фик, Фурье және Ньютон
заңдарын шығарып аламыз.
Молекулалар
қандай да бір көлемде біркелкі таралған
делік, олардың барлығы бір-бірінен
өздерінің механикалық параметрлері
бойынша ерекшеленеді. Молекулалардың
қандай да бір сортының концентрациясы
.
(10.7) теңдеудегі
шамасы
бір молекулаға қатысты сипаттама екенін
ескереміз