Добавлен: 02.02.2019
Просмотров: 13037
Скачиваний: 98
металдардың электр кедергісі еркін электрондардың иондармен соқтығысуына негізделген.
Осыларды ескеріп, Ом және Джоуль–Ленц заңдарының дифференциалды түрлерін қорытып шығаруға болады.
Ом заңы. Өткізгіште еркін электрондар электр өрісімен үдетіледі. Қозғалыс теңдеуі мына түрда жазылады :
![]() ,
,
мұндағы m – электрон массасы; а –электрон үдеуі;
е – электрон заряды.
Электрон қозғалысы бірқалыпты үдемелі болғандықтан, электрондардың реттелген қозғалысының орташа жылдамдығы:
![]() ,
(14.7)
,
(14.7)
ал ток тығыздығы –
![]() .
(14.8)
.
(14.8)
өрнектерімен анықталады.
![]() (14.9)
(14.9)
шамасы меншікті электр өткізгіштігі деп аталады, ал осыған кері шаманы
![]() –
меншікті
электр кедергісі деп атайды.
–
меншікті
электр кедергісі деп атайды.
Сәйкесінше ,
![]() .
(14.10)
.
(14.10)
(14.10) формуласы дифференцал түрдегі Ом заңын өрнектейді.
Джоуль–Ленц заңы. Электрон әр соқтығыста тордағы ионға электр өрісінің орташа энергиясын береді.
![]() .
(14.11)
.
(14.11)
Әр
электронның соқтығысу жиілігі
![]() ,
ал n
электрон үшін –
,
ал n
электрон үшін –
![]() .
.
Сондықтан токтың жылулық қуатының көлемдік тығыздығы төмендегідей өрнектеледі
![]() (14.12)
(14.12)
немесе
![]() .
(14.13)
.
(14.13)
(14.13) өрнегі дифференциал түрдегі Джоуль–Ленц заңы болып табылады.
Ток тығыздығы, электр өріс кернеулігі және жылу мөлшері арасындағы бұл байланыстар, яғни электр өткізгіштіктің классикалық теориясы сапалы дұрыс нәтиже бермеді. Бұл теорияның тәжірибелермен сәйкес келмейтін тұстары көп болды. Бірақ кванттық теорияда микробөлшектердің толқындық қасиеттерін ескеріп, бұл қиындықтардан шығар жол табылды.
15 дәріс . Вакуумдегі магнит өрісі
Дәріс мақсаты:
магнит өрісінің негізгі сипаттамаларымен танысу;
магнит өрісінің негізгі заңдарын оқып үйрену;
магнит өрісін есептеудің негізгі әдістерін үйрену.
15.1 Токтардың өзара әсерлесуі. Магнит индукция векторы. Суперпозиция принципі
Бір бағытта қозғалған зарядтар электр тогын туғызады, ал ток өздерін қоршаған кеңістіктің қасиеттерін өзгертіп, өзінің айналасында магнит өрісін тудырады. Магнит өрісі негізінен тогы бар өткізгішке әсер ететін күш арқылы білінеді. Магнит өрісін сипаттау үшін, оның тогы бар рамкаға тигізетін әсерін қолданамыз. Тогы бар рамка магнит өрісінде белгілі бір бұрышқа бұрылады. Рамканың айналу бағыты бойынша магнит өрісінің бағытын анықтай аламыз. Магнит өрісінің рамкаға бағдарлаушы әсері рамкада қос күшті тудырады. Осы қос күштің моментінің шамасы сыртқы магнит өрісінің индукциясына, рамкадағы ток күші мен өлшемдеріне және рамканың орналасуына тәуелді.
![]() ,
(15.1)
,
(15.1)
мұндағы
![]() -
контурдың нормаль бірлік векторы мен
магнит индукциясының арасындағы бұрыш.
Векторлық түрде былай жазылады
-
контурдың нормаль бірлік векторы мен
магнит индукциясының арасындағы бұрыш.
Векторлық түрде былай жазылады
![]() ,
(15.2)
,
(15.2)
![]() -
контурдың магнит моменті. Олай болса
айналдырушы момент
-
контурдың магнит моменті. Олай болса
айналдырушы момент
![]() .
(15.3)
.
(15.3)
Осыдан магнит индукциясының шамасы
![]() (15.4)
(15.4)
қатынасымен анықталады. Бағыты сыншы контурға түсірілген оң нормалдың тепе-теңдік бағытына сәйкес векторлық шама.
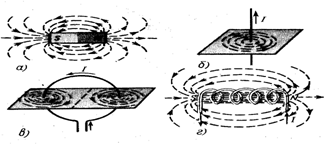
Магнит индукциясының күш сызықтары үшін, кез келген нүктедегі жанамасы осы нүктедегі индукция векторымен бағыттас сызықты аламыз. Магнит индукциясының күш сызықтарының электр өрісінің кернеулік сызықтарынан ерекшелігі - ол әр уақытта тұйық болады, 15.1 суретте әртүрлі жүйенің күш сызықтары көрсетілген. Тұйық болғандықтан оларды құйынды деп атайды.
|
|
|
|
|
|
15.1 Сурет
Магнит өрісі потенциалды емес, тұйық контур бойынша қозғалған зарядтың істейтін жұмысы нөлге тең емес. Магнит индукциясының бағыты оң бұранда ережесі бойынша анықталады. Өлшем бірлігі тесла (Тл).
Суперпозиция
принципі
- егер
берілген кеңістік нүктесінде әртүрлі
токтар
![]() магнит
өрістерін туғызса, онда осы нүктедегі
қорытқы магнит өрісі олардың векторлық
қосындыларымен анықталады:
магнит
өрістерін туғызса, онда осы нүктедегі
қорытқы магнит өрісі олардың векторлық
қосындыларымен анықталады:
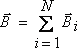 .
(15.5)
.
(15.5)
15.2 Био–Савар–Лаплас заңы. Магнит индукциясы векторының циркуляциясы туралы теорема. Қарапайым жүйелердің магнит өрістерін есептеу
Био-Савар-Лаплас заңы - кез келген I тогы бар өткізгіштің dl элемент өрісінің бір нүктесіндегі магнит өрісінің бағыты мен шамасын анықтайды. Осы заңға сәйкес I тұрақты электр тогының вакуумдегі магнит өрісі келесі өрнекті қанағаттандыруы тиіс
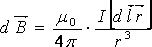 (15.6)
(15.6)
модулі
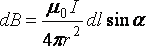 ,
(15.7)
,
(15.7)
мұндағы
![]() –
ток
элементінің тудыратын магнит өрісінің
магнит индукция векторы;
–
ток
элементінің тудыратын магнит өрісінің
магнит индукция векторы;
![]() -
ток
тығыздық векторының бағытымен сәйкес
келетін ток элементі;
-
ток
тығыздық векторының бағытымен сәйкес
келетін ток элементі;
![]() –
осы
элементпен өрістің қарастырылған С
нүктесін қосатын радиус-векторы,
(15.2 суретті
қара);
–
осы
элементпен өрістің қарастырылған С
нүктесін қосатын радиус-векторы,
(15.2 суретті
қара);
![]() Гн/м
– магнит
тұрақтысы;
I
– өткізгіштегі
ток күші.
Гн/м
– магнит
тұрақтысы;
I
– өткізгіштегі
ток күші.
![]() векторы
С нүктесінде оң бұранда ережесі бойынша
векторы
С нүктесінде оң бұранда ережесі бойынша
![]() және
және
![]() векторлар
жазықтығына перпендикуляр бағытталған.
векторлар
жазықтығына перпендикуляр бағытталған.
|
|
|
|
|
|
Іdl r
15.2 Сурет
15. 3 Магнит ағыны. Магнит өрісі үшін Гаусс теоремасы
Магнит
өрісі электр өрісі сияқты екі негізгі
қасиетке ие. Бұл қасиеттер
![]() векторлық
өрістің ағынымен және циркуляция
векторымен байланысты және магнит
өрісінің негізгі заңдарын өрнектейді.
векторлық
өрістің ағынымен және циркуляция
векторымен байланысты және магнит
өрісінің негізгі заңдарын өрнектейді.
Магнит ағыны – скаляр шама, магнит индукция векторының жазықтық бетінің ауданына көбейтіндісімен анықталады
![]() ,
(15.7)
,
(15.7)
мұндағы
d![]() =
=
![]() d
d![]() ;
;
![]() –
dS
ауданға түсірілген бірлік вектор
;
–
dS
ауданға түсірілген бірлік вектор
;
Вn
– нормал
бағыттағы
![]() векторының
проекциясы.
векторының
проекциясы.
Бүкіл бет арқылы өтетін магнит ағыны
![]() .
(15.8)
.
(15.8)
Егер
магнит өрісі бір текті болса
![]() .
Өлшем бірлігі Вебер
[Вб].
Магнит ағыны косинус бұрышының таңбасына
байланысты оң немесе теріс мәндер
қабылдайды, яғни оның бағыты
.
Өлшем бірлігі Вебер
[Вб].
Магнит ағыны косинус бұрышының таңбасына
байланысты оң немесе теріс мәндер
қабылдайды, яғни оның бағыты
![]() нормал
вектордың оң бағытына сәйкес анықталады.
(15.3 суретті қара)
нормал
вектордың оң бағытына сәйкес анықталады.
(15.3 суретті қара)
|
|
|
|
|
|
15.3 Сурет
Гаусс теоремасы – кез келген тұйық бет арқылы өтетін магнит ағыны әр
уақытта нөлге тең болады
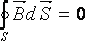 .
( 15.9)
.
( 15.9)
Осыдан шығатыны табиғатта (электр зарядтары сияқты) магнит зарядтары (магнит өрісінің көзі) болмайтындығын көрсетеді.
Тұрақты
ток магнит өрісінің контур бойынша
![]() векторының
циркуляциясы
векторының
циркуляциясы
![]() -магнит
тұрақтысымен осы контур қамтитын барлық
токтардың алгебралық қосындысының
көбейтіндісіне тең
-магнит
тұрақтысымен осы контур қамтитын барлық
токтардың алгебралық қосындысының
көбейтіндісіне тең
![]() .
(15.10)
.
(15.10)
Жоғарыда айтылғандай магнит өрісі потенциалды емес, екінші сөзбен айтқанда магнит индукциясының циркуляциясы нөлге тең емес, яғни магнит өрісі құйынды өріс екенін білдіреді. (15.4) өрнегі кейбір токтар конфигурацияларының өрісін есептеуге қолданылады.
15.4 Магнит өрісінде тогы бар өткізгіш пен тогы бар контур орын ауыстырғанда істелетін жұмыс
Магнит өріс күшінің тогы бар контурдың орнын ауыстыруда жасаған элементар жұмысы контурдағы ток күші мен осы контурмен шектелген аудан арқылы өтетін магнит ағынының өзгерісінің көбейтіндісіне тең.
![]() .
(15.11)
.
(15.11)
Тогы бар контурдың орнын бастапқы 1 жағдайдан 2 жағдайға орнын ауыстырғанда жасалынатын толық жұмыс мына формуламен анықталады
![]() .
(15.12)
.
(15.12)
тұрақты ток жағдайында
![]() .
(15.13)
.
(15.13)
16 дәріс . Зат ішіндегі магнит өрісі
Дәріс мақсаты:
зат ішіндегі магнит өрісінің негізгі сипаттамаларымен танысу;
заттардағы магнит өрісін есептеудің негізгі әдістерін үйрену.
16.1 Магнетик түрлері. Диамагнетиктер, парамагнетиктер, ферромагнетиктер
Кез келген зат магнетик болып табылады. Олар сыртқы магнит өрісінде магниттелініп, өздерінің магнит өрістерін тудырады. Сыртқы магнит өрісі болмағанда атомдардың магнит моменттері ретсіз орналасады, сондықтан магнит мометінің қорытқы орташа мәні нөлге тең. Заттардағы қорытқы магнит өрісінің индукция векторы:
![]() ,
(16.1)
,
(16.1)
мұндағы
![]() –
сыртқы магнит өрісінің индукция векторы
(өткізгіштік ток өрісі);
–
сыртқы магнит өрісінің индукция векторы
(өткізгіштік ток өрісі);
![]() –
магниттелген
заттың тудыратын меншікті (ішкі) магнит
өріс индукциясы.
–
магниттелген
заттың тудыратын меншікті (ішкі) магнит
өріс индукциясы.
Заттың
магниттелінуі
бірлік
көлемдегі магнит моментімен сипатталады,
оны
![]() магниттеліну
векторы
деп атайды. Берілген
магниттеліну
векторы
деп атайды. Берілген
![]() элементар
көлемдегі магниттеліну векторы:
элементар
көлемдегі магниттеліну векторы:
![]() ,
(16.2)
,
(16.2)
мұндағы
![]() –
магнетиктің қарастырылған нүктесінің
аймағынан алынған элементар көлем;
–
магнетиктің қарастырылған нүктесінің
аймағынан алынған элементар көлем;
![]() –
осы
көлемдегі жеке молекулалардың магнит
моменті.
–
осы
көлемдегі жеке молекулалардың магнит
моменті.
16.2 Магниттелінгіштік. Магнит өрісінің кернеулігі. Зат ішіндегі магнит өрісі үшін толық ток заңы
Гаусс теоремасы. Магниттелген заттардың өрісінің өткізгіштік токтардың өрісі сияқты көздері болмайды. Сондықтан Гаусс теоремасы вакуумдегі өрістегідей өзгеріссіз жазылады
![]() .
(16.3)
.
(16.3)
Сондықтан
![]() векторының
сызықтары барлық жерде үздіксіз болады.
векторының
сызықтары барлық жерде үздіксіз болады.
![]() векторының
циркуляциясы туралы теорема.
Магнетиктерде циркуляция векторы
векторының
циркуляциясы туралы теорема.
Магнетиктерде циркуляция векторы
![]() өткізгіштік
токтармен қатар
өткізгіштік
токтармен қатар
![]() магниттелу
токтарымен анықталады
магниттелу
токтарымен анықталады
![]() .
(16.4)
.
(16.4)
Осы өрнектерді ескеріп алатынымыз
![]() .
(16.5)
.
(16.5)
Интеграл астындағы шама
![]() (16.6)
(16.6)
магнит өрісінің кернеулігі деп аталады. Бұл шаманың физикалық мағынасы жоқ, оның көмегімен біртексіз ортадағы магнит өрісінің теңдеулерін ыңғайлы түрде жазуға болады.
![]() векторының
циркуляция теоремасы:
тұйықталған контур бойымен алынған
векторының
циркуляция теоремасы:
тұйықталған контур бойымен алынған
![]() векторының
циркуляциясы осы контурмен шектелген
өткізгіштік токтардың алгебралық
қосындысына тең
векторының
циркуляциясы осы контурмен шектелген
өткізгіштік токтардың алгебралық
қосындысына тең
![]() .
(16.7)
.
(16.7)
Тәжірибеден
магниттелу векторы магнит өрісінің
кернеулігіне тура пропорционал
![]() ,
мұндағы
,
мұндағы
![]() -
заттың магнит қабылдағышы.
-
заттың магнит қабылдағышы.
![]() шамасы
оң және теріс шама болуы мүмкін.
шамасы
оң және теріс шама болуы мүмкін.
Осы
қатынастарды пайдаланып,
![]() және
және
![]() векторларының
арасындағы
векторларының
арасындағы
![]() (16.8)
(16.8)
байланысты анықтауға болады.
Парамагнетиктер
үшін
![]() ,
диамагнетиктер үшін
,
диамагнетиктер үшін
![]() .
Диа- және парамагнетиктерде
.
Диа- және парамагнетиктерде
![]() бірден
аз ғана өзгерісте болады, сондықтан бұл
магнетиктердің магниттік қасиеттері
айтарлықтай күшті болмайды.
бірден
аз ғана өзгерісте болады, сондықтан бұл
магнетиктердің магниттік қасиеттері
айтарлықтай күшті болмайды.
Барлық магнетиктер магнит қабылдағыштарына және оның таңбаларына қарай үш топқа бөлінеді:
Прамагнетиктер
-
![]() сыртқы
магнит өрісі мен
сыртқы
магнит өрісі мен
![]() өздік
магнит өрістері бағыттас болып, магнит
қабылдағышы
өздік
магнит өрістері бағыттас болып, магнит
қабылдағышы
![]() және
және
![]() аралығында
жататын, температураға байланысты
өзгереді. Парамагнетиктерге мынандай
заттар жатады:
аралығында
жататын, температураға байланысты
өзгереді. Парамагнетиктерге мынандай
заттар жатады:
![]() ,
сілтілер т.б.
,
сілтілер т.б.
Диамагнетиктер-
![]() сыртқы
магнит өрісі мен
сыртқы
магнит өрісі мен
![]() өздік
магнит өрістері қарама-қарсы болып,
өздік
магнит өрістері қарама-қарсы болып,
![]() және
және
![]() аралығында
жатады, температураға байланысты емес.
Диамагнетиктерге мына заттар жатады:
инертті газдар,
аралығында
жатады, температураға байланысты емес.
Диамагнетиктерге мына заттар жатады:
инертті газдар,
![]() ,
су, шыны т.б.
,
су, шыны т.б.
Ферромагнетиктер-![]() ,
,
![]() ,
,
![]() және
температураға байланысты өзгереді.
Диамагнетиктерге мына заттар жатады:
темір, никель, кобальт т.б.
және
температураға байланысты өзгереді.
Диамагнетиктерге мына заттар жатады:
темір, никель, кобальт т.б.
Ферромагнетиктердің магнит қабылдағыштығы сыртқы өріс кернеулігіне байланысты.
16.4 Екі магнетик шекарасында орындалатын шарттар
Орталардың
шекарасында магнит өрісінің екі
![]() және
және
![]() векторлық
сипаттамаларының бағыттары мен шамалары
секірмелі түрде өзгереді. Бұл векторлар
үшін шекаралық шарттар электр өрісіндегідей
қорытылып шығарылады және төмендегі
формулалармен өрнектеледі
векторлық
сипаттамаларының бағыттары мен шамалары
секірмелі түрде өзгереді. Бұл векторлар
үшін шекаралық шарттар электр өрісіндегідей
қорытылып шығарылады және төмендегі
формулалармен өрнектеледі
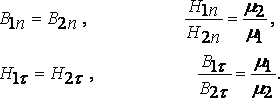 (16.9)
(16.9)
![]() және
және
![]() векторларының
құраушылары үшін алынған екі диэлектрик
шекарасындағы шекаралық шарттар бұл
векторлардың сызықтары сынатынын,
нәтижесінде
векторларының
құраушылары үшін алынған екі диэлектрик
шекарасындағы шекаралық шарттар бұл
векторлардың сызықтары сынатынын,
нәтижесінде
![]() бұрышының
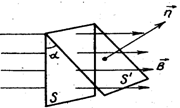
өзгеретінін көруге болады (16.2 суретті
қара).
бұрышының
өзгеретінін көруге болады (16.2 суретті
қара).
|
|
|
15.4 Сурет
Біртекті емес ортадағы магнит өрісін есептеуге толық ток және шекаралық шарттар қолданылады.
2010 ж.жиынтық жоспары, реті 233
Коммерциялық емес акционерлік қоғам
АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ
Физика кафедрасы
ФИЗИКА 2
5В071900 – Радиотехника, электроника және телекоммуникациялар, 5В070400- Есептеу техникасы және бағдарламалық қамтамасыз ету,
5В070300- Ақпараттық жүйелер мамандықтарының барлық бөлімінде оқитын студенттерге арналған
дәрістер жинағы
Алматы 2012
ҚҰРАСТЫРҒАНДАР: Байпақбаев Т.С., Қызғарина М.Т., Мамырбаева Г.А. Физика 2. 5В071900 – Радиотехника, электроника және телекоммуникациялар, 5В070400 - Есептеу техникасы және бағдарламалық қамтамасыз ету, 5В070300 - Ақпараттық жүйелер мамандықтарының барлық бөлімінде оқитын студенттерге арналған дәрістер жинағы. - Алматы: АЭжБУ, 2012. - 62 б.
Бакалавриаттың энергетика мамандықтары үшін «Физика 2» пәні бойынша дәрістердің қысқаша мазмұны берілген.
«Физика 2 дәрістер жинағы» пән бойынша оқу үдерісін әдістемелік қамтамасыз ету жүйесінің бір элементі болып табылады және дәрістік сабақтарда, сондай-ақ студенттердің өзіндік жұмысында теориялық материалмен жұмыс істеуде, машықтандыру, зертханалық сабақтарына және емтиханға дайындық кезінде таратпа материал ретінде қолдануға болады. Студенттер мен жас оқытушыларға ұсынылады.
Без. 30, кесте. 5, әдеб. көр.- 5 атау.
Пікір беруші: физ.-мат. ғыл. канд., доцент Дауменов Т.Д.
«Алматы энергетика және байланыс университетінің» КЕАҚ 2012 жылғы жоспары бойынша басылады.
«Алматы энергетика және байланыс университеті» КЕАҚ, 2012 ж.
Мазмұны
Кіріспе 5
1 Дәріс. Электрмагниттік индукция 6
1.1 Электрмагниттік индукция заңы 6
1.2 Өздік индукция заңы. Экстратоктар 6
1.3 Өзара индукция құбылысы 8
1.4 Магнит өрісінің энергиясы 9
2 Дәріс. Максвелдің теориясының негіздері 9
2.1 Құйынды электр өрісі 10
2.2 Ығысу тогы 10
2.3 Максвелл теңдеулерінің жүйесі 11
3 Дәріс. Тербелмелі процестер 12
3.1 Еркін гармоникалық тербелістер 13
3.2 Гармоникалық тербелістердің энергиясы 14
4 Дәріс. Тербелістерді қосу.Өшетін және еріксіз тербелістер 14
4.1 Бірдей бағыттағы тербелістерді қосу 15
4.2 Өзара перпендикуляр тербелістерді қосу 16
4.3 Еркін өшетін электромагниттік тербелістер 17
4.4 Еріксіз электромагниттік тербелістер. Резонанс 18
5 Дәріс. Толқындық процестер 20
5.1 Серпімді толқындар 20
5.2 Толқынның теңдеуі 21
5.3 Толқындық теңдеу 22
5.4 Толқынның теңдеуі. Умов векторы 22
6 Дәріс. Электрмагниттік толқындар 24
6.1 Электрмагниттік толқынның дифференциалдық теңдеуі 24
6.2 Электрмагниттік толқынның энергиясы. Пойнтинг векторы 25
6.3Электрмагниттік толқынның сәуле шығаруы 26
7 Дәріс. Толқындық оптика 27
7.1 Жарық толқыны 27
7.2 Жарық интерференциясы. Когеренттілік 28
7.3 Жарық дифракциясы 30
7.4 Жарық поляризациясы 31
8 Дәріс. Электрмагниттік сәуле шығарудың кванттық табиғаты 31
8.1 Жылулық сәуле шығарудың сипаттамалары мен қасиеттері 31
8.2 Абсолют қара дененің жылулық сәуле шығару заңдары 33
8.3 Рэлей-Джинс формуласы. Ультракүлгін апаты 34
8.4 Планктың кванттық гипотезасы және формуласы 34
9 Дәріс. Электрмагниттік сәуле шығарудың корпускулалық қасиеттері 35
9.1 Фотондар 35
9.2 Фотоэффект 36
9.3 Комптон эффекті 37
9.4 Электрмагниттік сәуле шығарудың
корпускулалық-толқындық дуализмі 38
10 Дәріс. Зат қасиеттерінің корпускулалық-толқындық дуализмі 39
10.1 Де Бройль гипотезасы 39
10.2 Гейзенбергтің анықталмағандық қатынасы 40
10.3 Де Бройль толқынының статистикалық түсіндірмесі 41
11 Дәріс. Шредингер теңдеуі және оның шешімдері 42
11.1 Кванттық механикадағы бөлшектің күйі. Толқындық функция 42
11.2 Шредингер теңдеуі 43
11.3 Шредингер теңдеуін шешу мысалдары 44
11.4 Бордың сәйкестік принципі 47
12 Дәріс. Сутегі атомы үшін Шредингер теңдеуінің шешімі 47
12.1 Сутегі атомының энергетикалық спектрі 48
12.2 Орбиталды және магниттік кванттық сандар 48
12.3 Сутегі атомының оптикалық спектрі 50
12.4 Электрон спині 50
13 Дәріс. Кванттық статистикалар және оларды қолдану 51
13.1 Ұқсас бөлшектердің ажыратылмаушылығы. Паули қағидасы 51
13.2 Кванттық үлестірілулер 52
13.3 Металдағы электрондар үшін Ферми-Дирак үлестірілуі 53
14 Дәріс. Қатты денелердің аймақтық теориясы 55
14.1 Кристалдағы электрондардың энергетикалық
спектрінің аймақтық құрылымы 55
14.2 Металл, диэлектрик және шалаөткізгіштердегі
энергетикалық аймақтар 56 14.3 Шалаөткізгіштердің өткізгіштігі 57
15 Дәріс. Ядролық физика 58
15.1 Атом ядросының құрамы және сипаттамалары 58
15.2 Ядроның массасы және байланыс энергиясы 59