Полярлы диэлектриктерде диэлектрлік қабылдағыштық температураға кері пропорционал. Кристалды диэлектриктерде де полярлану –өріс кернеулігімен (12.4) қатынастағыдай байланыста. мен арасындағы сызықты тәуелділік күшті емес өрістерде орындалады. Кейбір диэлектриктерге (12.4) өрнегі қолданылмайды. Сегнетоэлектриктерде (сыртқы электр өрісінің әсерінсіз белгілі бір температура аралығында өздігінен поляризацияланатын кристалл диэлектриктер, NaKC₄H₄O₆*4H₂O - сегнет тұзы, BaTiO₃ – барий титанаты) мен арасындағы байланыс сызықсыз және -нің бұрынғы мәндеріне де тәуелді (бұл құбылыс гистерезис деп аталады).

Диэлектрикті сыртқы өріске орналастырса, ол 12.1 суреттегідей оң зарядтар өріс бағытымен, теріс зарядтар өріс бағытына қарама-қарсы бағытта полярланады, нәтижесінде диэлектрик пластиналарының (оң жақ) бетінде беттік тығыздығы , ал (сол жақ) оған қарама-қарсы бетінде беттік тығыздығы болатын артық зарядтар пайда болады. Бұл зарядтар байланысқан беттік зарядтар деп аталады. Олар диэлектриктердің атомдары мен молекулаларынан бөлініп кетпейді.

Полярлану векторы мен байланысқан зарядтардың беттік тығыздығы бір-бірімен қарапайым байланысқан

(12.5)

(12.4) өрнегін ескеріп, мына формулаға келеміз:

, (12.6)

мұндағы –беттің берілген нүктесіндегі сыртқы нормальдағы полярлану проекциясы; – өріс кернеулігінің сол нормальдағы проекциясы.

12.2 Диэлектриктердегі электрстатикалық өріс үшін Гаусс теоремасы. Электр ығысу векторы

Электрстатикалық өрістің көзі еркін зарядтармен қатар байланысқан зарядтар да болып табылады. Сондықтан өрісі үшін Гаусс теоремасын төмендегідей жазуға болады

, (12.7)

мұндағы – ауданы S бетпен қамтылған көлемдегі еркін және байланысқан зарядтардың алгебралық қосындысы.

Өріс кернеулік векторын табуға (12.7) өрнегі тиімсіздеу, өйткені өріске тәуелді байланысқан зарядтардың таралуы алдын ала берілмеген.

Өрісті есептеу көп жағдайда қосымша шаманы енгізумен жеңілдетіледі. Ол шаманың көзі тек еркін зарядтар болып табылады және электрлік ығысу немесе электр индукциясы деп аталады:

. (12.8)

Ығысу векторы екі түрлі физикалық шамалардың қосындысынан тұрады: және , сондықтан ол көмекші вектор, оның қандай да бір физикалық мағынасы жоқ, көп жағдайда диэлектриктердегі электр өрісін оқып үйренуге жеңілдік жасайды.

Тұйықталған бет арқылы өтетін электр ығысу векторының ағыны осы бет ішіндегі еркін зарядтардың алгебралық қосындысына тең:

. (12.9)

Бұл электр ығысу векторы үшін Гаусс теоремасы. (12.4) өрнектегі мәнін (12.8) өрнегіне қойып алатынымыз

немесе

, (12.10)

мұндағы –диэлектриктің негізгі электрлік сипаттамасы болып табылатын заттың диэлектрлік өтімділігі.

Электрлік ығысудың өлшем бірлігі – Кл/м².

12.3 Екі диэлектрик шекарасы бөлігіндегі шарттар

Біртекті изотропты екі диэлектрик шекарасында және векторлары электрстатиканың негізгі теоремаларымен анықталады: векторының (11.18) циркуляциясы туралы теорема және векторы үшін Гаусс (12.9) теоремасы

---

, .

векторының (11.18) циркуляциясы туралы теорема бойынша

, , (12.11)

векторының тангенциал құраушысы шекаралық бетке жақын жерде екі жақта да өзгермейді, ал векторының тангенциал құраушысы шекаралықтан өткенде секірмелі болып өзгереді.

Гаусс теоремасынан келесі қатынастарды аламыз:

, . (12.12)

Бұл қатынастардан шығатыны: векторының нормал құраушысы шекаралықтан өткенде өзгермейді, ал векторының нормал құраушысы үзіліске ұшырайды.

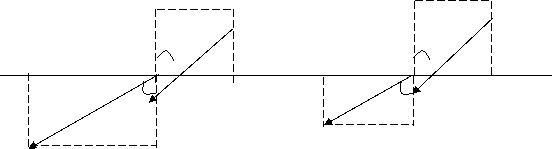Екі біртекті изотропты диэлектрик шекарасындағы және векторларының құраушылары үшін алынған (12.11) және (12.12) қатынастары осы вектор сызықтары сынатынын білдіреді. Осының салдарынан беттің шекарасына түсірілген нормал мен сызықтарының арасындағы бұрышы өзгереді ( 11.2 суретті қара).

12.2 Сурет.

және векторларының екі диэлектрик шекарасындағы сынуы ( )

Алынған шарттарды ескеріп, электрстатикалық өріс кернеулік вектор сызықтарының екі диэлектрик ортаның шекаралық бетіндегі сыну заңы

(12.13)

формуласымен өрнектеледі.

13-дәріс. Электростатикалық өрістегі өткізгіштер

Дәрістің мақсаты:

- өткізгіш ішіндегі электр өрісі;

- конденсаторлар туралы;

- өткізгіштердегі электр энергиясы туралы оқып үйрену.

13.1 Зарядтардың өткізгіш бетінде таралуы. Өткізгіш ішіндегі электр өрісі

Өткізгіштер деп оларда электр зарядтарының реттелген қозғалысы бола алатын заттарды айтады. Өткізгіштердің электр зарядтарын өткізу қабілеті оларда зарядтың еркін тасымалдаушыларының болуымен түсіндіріледі. Өткізгіштердің мысалына металдар, тұздар мен қышқылдардың судағы ерітінділері, иондалған газдар және т.б. жатады.

Егер металл өткізгіш электр өрісіне орналастырылса, онда осы өрістің

әсерімен өткізгіш электрондар жылулық бейберекет қозғалыспен қатар тәртіптелген қозғалысқа түсіріледі және өріс кернеулігіне қарсы бағытта орын ауыстырады.

Сонда өткізгіштің сол жақ бетінде артық теріс заряд, ал қарама-қарсы оң

жақ бетінде артық оң заряд пайда болады. Өткізгіш беттерінде пайда болған зарядтар, оның ішінде кернеулігі сыртқы электр өрісінің кернеулігіне қарсы бағытталған электр өрісін тудырады. Өткізгіштегі қорытқы электр өрісінің кернеулігі , болған кезде өткізгіштерге электрондарға әсер ететін күш нөлге тең болады да, ондағы зарядтардың реттелген қозғалысы тоқталады .

Өріс жоқ дейтін себебіміз, өткізгіште сыртқы көзден алынған энергияны

шығындамай зарядтардың реттелген қозғалысы болуы мүмкін емес, бұл энергияның сақталу заңына қарама-қайшы келеді.

Бұдан шығатыны , яғни зарядталған өткізгіштің ішіндегі барлық нүктелерінде оның потенциалы бірдей, зарядты өткізгіштің беті эквипотенциал бет болып табылады. Беттің кернеулік векторы осы беттің әрбір нүктесіне нормаль бойымен бағытталады.

Электр өрісінде орналасқан өткізгіште әр аттас зарядтардың бөліну құбылысы электрстатикалық индукция деп аталады. Өткізгішті өрістен алып кетсе, электрстатикалық өріс әсерінен бөлінген зарядтар – индукцияланған зарядтар өзара теңгеріледі, бұл кезде металл өзінің бұрынғы қалыпты күйіне келеді.

---

Егер өткізгіштің ішінде қуыс болса, онда өткізгіштен тыс қандай өрістің болуына және өткізгіштің қалай зарядталғанына байланыссыз осы қуыстағы өрістің кернеулігі нөлге тең болады. Электрстатикалық қорғау құбылысы осы қағидаға негізделген: егер құрал тұйық металл бетпен қоршалса, онда оған ешқандай сыртқы электр өрістері әсер етпейді.

Сонымен өткізгіштерге мынадай қасиеттер тән:

- өткізгіш ішінде электрстатикалық өріс болмайды, ;

- статикалық зарядтардың барлығы өткізгіш бетінде болады, (мұндағы - зарядтардың беттік тығыздығы, - өткізгішті қоршап тұрған ортаның диэлектрлік өтімділігі);

- өткізгіш бетіндегі кернеулік векторы осы бетке перпендикуляр бағытталады.

13.2 Электр зарядтарының өзара әсерлесу энергиясы. Зарядталған өткізгіш пен конденсатор энергиясы

Бөлшектер жүйесінің әсерлесу энергияларының өзгерісі нәтижесінде осы бөлшектердің өзара орын ауыстыру жұмыстары жасалынады. Ол бөлшектердің өзара әсерлесу заңдылықтарына және орналасуларына тәуелді. Сан жағынан бұл энергия әсерлесу күштерінің жүйедегі барлық бөлшектерді бір-бірінен шексіздікке орнын ауыстыруға жұмсалған жұмысына тең. Егер бөлшектер жүйесіндегі әрқайсысының өрістегі энергиялары W₁₂ және W₂₁ болса, онда олар өзара тең W₁₂=W₂₁=W_р, сондықтан екі бөлшектің әсерлесу энергиясы төмендегідей жазылады

(13.1)

Сәйкесінше жүйедегі барлық әсерлесуші бөлшектер жүйесі үшін

(13.2)

деп жазуға болады. Мұндағы – i-ші бөлшектің жүйедегі қалған барлық бөлшектердің өрісіндегі потенциалды энергиясы.

Потенциалдың (11.19) анықтамасы бойынша әсерлесуші нүктелік зарядтар жүйесі үшін алатынымыз

(13.3)

мұндағы – жүйедегі барлық зарядтардың q_i заряд орналасқан нүктедегі толық потенциалы.

Егер заряд V көлем бойынша көлемдік тығыздықпен үздіксіз таралатын болса, онда зарядтар жүйесін элементар зарядтардың жиынтығы ретінде қарастырып, (13.3) қосындыдан интегралдауға өтеміз

, (13.4)

мұндағы – жүйедегі барлық зарядтардың көлем бөлігінде тудыратын потенциалы.

Өткізгіштің q заряды мен потенциалы болсын. Өткізгіштің беті

эквипотенциал болғандықтан (13.4) потенциалды интегралдың сыртына шығаруға болады. Сонымен, зарядталған өткізгіш энергиясы:

, (13.5)

мұндағы - өткізгіш зарядын оның потенциалына қатынасымен өлшенетін физикалық шама – зарядталған өткізгіштің сыйымдылығы. ХБ жүйесіндегі өлшем бірлігі – фарад (Ф).

Зарядталған өткізгіш энергиясы оны зарядтауға кеткен сыртқа күштердің жұмысына тең.

Конденсатор тең әр аттас зарядтармен зарядталған екі өткізгіштен тұрады. Конденсаторды құрайтын өткізгіштер оның астарлары деп аталады.

Зарядталған конденсатордың энергиясы екі өткізгіштен тұратын жүйенің толық энергиясы болып табылады:

, (13.6)

мұндағы q – конденсатордың заряды, С – оның сыйымдылығы, U – конденсатор астарларының арасындағы потенциалдар айырымы.

---

13.3 Электрстатикалық өріс энергиясы. Электрстатикалық өріс энергиясының көлемдік тығыздығы

Зарядталған жазық конденсаторды қарастырамыз. Оның энергиясы (13.6) формуласымен, ал электр сыйымдылығы

. (13.7)

өрнегімен анықталады.

Егер конденсатор астарларының ара қашықтығы оның өлшемдерінен айтарлықтай аз болса, онда конденсатор энергиясын біртекті деп қарастыруға болады. Сонда , осы және (13.5) өрнектерін (13.6) формуласына қойып, алатынымыз:

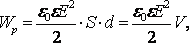(13.8)

мұндағы жазық конденсатордағы өрістің алып тұрған көлемі. Бұл формулада конденсатор энергиясы электр өрісін сипаттайтын

өріс кернеулігімен өрнектелген. Осы жағдайда энергия таралған көлем бойынша осы энергияны тасымалдаушы рөлін өріс атқарып тұр. Тұрақты өріс және оған себепші зарядтар бір-бірімен тікелей байланыста. Алайда уақыт бойынша өзгеретін өріс өзін тудырушы зарядтарға байланыссыз болады да кеңістікте электрмагнитті толқын ретінде тарай береді. Тәжірибе электромагнитті толқын энергия тасымалдайтынын көрсетті.

Атап айтқанда, Жер бетіндегі тіршілікке керекті энергия Күннен электрмагнитті толқындар арқылы (жарықпен) жеткізіледі, радиоқабылдағыштарды сөйлететін энергиялар орталық станциядан электрмагнитті толқындармен жеткізіледі т.с.с. Осы фактілер энергия тасымалдаушылар өріс екендігін білдіреді.

Электрстатикалық өріс энергиясының көлемдік тығыздығын (13.8) өрнегін пайдаланып мына түрде алуға болады

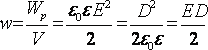. (13.9)

Изотропты диэлектриктерде және векторларының бағыттары бағыттас, сондықтан (13.9) формуласындағы -ны -ге алмастырып, алатынымыз:

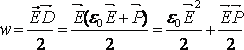. (13.10)

Бірінші қосынды вакуумдегі, екіншісі диэлектрикті полярлауға кеткен өріс энергия тығыздығын сипаттайды.

Әрбір нүктедегі өріс энергиясының тығыздығын білсек, төмендегі интеграл көмегімен бүкіл V көлемдегі энергияны табуға болады.

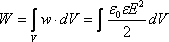. (13.11)

Бұл біртекті және біртекті емес электрстатикалық өрісті, сонымен қатар айнымалы потенциалды емес өрісті есептеуге пайдалынатын әмбебап формула.

14 дәріс . Тұрақты электр тогы

Дәріс мақсаты:

 тұрақты электр тогының негізгі сипаттамаларын оқып үйрену;

 тұрақты электр тогы заңдарын оқып үйрену;

 металдардың электр өткізгіштігінің классикалық теориясын меңгеру және одан электр тогының негізгі заңдарын қорыту.

14.1 Токтың жалпы сипаттамалары және бар болу шарттары

Электр тогы - зарядталған бөлшектер мен макроскопиялық денелердің реттелген қозғалысы.

Токтың болу шарттары: ортада ток тасымалдаушылардың және электр өрісінің болуы.

Токты ұстап тұру үшін міндетті түрде қандай да бір энергияны электр тогының энергиясына айналдыруына негізделген электр энергиясының көзі болуы қажет.

Электр тогының сандық сипаттамасы – ток күші. Ток күші– бірлік уақытта қарастырылған бет арқылы өтетін зарядтармен анықталатын скаляр физикалық шама.

. (14.1)

Ток күші және оның бағыты уақытқа байланысты өзгермесе, ондай ток тұрақты ток деп аталады және .

---

Электр тогы тұрақты болуы үшін ток өтетін өткізгіштің барлық нүктесіндегі электр өрісінің кернеулігі өзгермеуі қажет. Яғни осы өткізгіште зарядтар бір жерінде азайып, бір жерінде жиналып қалмауы қажет. Бұл шарт тұрақты ток тізбегі тұйықталған және тізбектің барлық көлденең қимасындағы ток күші бірдей болуы керек екендігін білдіреді.

Қарастырылған беттің әртүрлі нүктесіндегі электр тогының бағыты және оның таралуы ток тығыздығының векторы деп аталатын физикалық шамамен сипатталады.

Ток тығыздығы- ток бағытына перпендикуляр беттің бірлік аудан арқылы өтетін ток күшімен анықталады

. (14.2)

Бұл өрнектен беттен өтетін ток күші осы беттен өткен ток тығыздығының векторының ағынына тең екені шығады

. (14.3)

Ток тығыздығын өткізгіштегі зарядтардың реттелген қозғалысының жылдамдығы, ток тасмалдаушылардың концентрациясы және тасымалдаушылардың элементар заряды арқылы төмендегідей өрнектеуге болады

. (14.4)

14.2 Стационар электр тогы. Үздіксіздік теңдеуі

Егер ток өтіп жатқан өткізгіш ортадан ойша тұйықталған бет алатын болсақ, (13.3) өрнегі бойынша, осы бет арқылы өтетін ток тығыздық векторының ағыны осы бетпен шектелген аймақтан өтетін ток күшіне тең.

Зарядтың сақталу заңына сәйкес бұл интеграл бірлік уақыттағы шектелген көлем ішіндегі зарядтың кемуіне тең

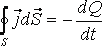. (14.5)

Осы қатынас үздіксіздік теңдеуі деп аталады.

Тұрақты ток үшін кеңістіктегі токтың таралуы өзгермейді, сондықтан . Осыдан шығатыны тұрақты ток үшін вектор сызықтарының еш жерден басталмайды және еш жерден аяқталмайды, олар тұйықталған сызықтар, яғни векторының өрісінің көзі жоқ.

14.3 Металдардың электрөткізгіштігінің классикалық және электрондық теориясы және оның қолдану шегі. Дифференциалдық түрдегі Ом және Джоуль-Ленц заңдары

К. Рикке (1901), С.Л. Мандельштам и Н.Д. Папалекси (1913), Р. Толмена және Б. Стюарт (1916) тәжірибелерінде металдардағы ток тасымалдаушылар еркін электрондар, яғни металл кристалдарындағы иондарымен әлсіз байла-нысқан электрондар екені анықталды. Еркін электрондардың концентрациясы шамамен .

Еркін электрондар ұғымынан кейін П. Друде және Х. Лоренц металдардың классикалық теориясын құрды. Друде–Лоренц теориясы бойынша:

 өткізгіштік электрондары идеал газ молекулалары сияқты қарастырылады;

 электрондардың жылулық қозғалысының орташа жылдамдығы формуласымен анықталады;

 электрондар бір-бірімен емес, металдардың кристалдық торларын құрайтын иондармен соқтығысады;

 электрондардың реттелген қозғалысының орташа жылдамдығы жылулық қозғалыстың орташа жылдамдығынан шамасындай аз, электрондардың еркін жүруінің орташа уақыты төмендегі формуламен анықталады:

, (14.6)

мұндағы – электрондардың еркін жүру жолының орташа ұзындығы;

 электрондар иондармен соқтығысқанда реттелген қозғалысының жылдамдығынан толығымен айырылып, энергиясын кристалды торларға береді, нәтижесінде металдың ішкі энергиясы арттырады және қызады;

---

Смотрите также файлы

• Физика дәріс.docx

• Философия методичка рус.doc

• Философия.docx

• Электротехникалық материалтану зертаханалық жұмыс 3,4.docx

• Электростатика.doc