ОтчётПо лабораторной работе №1По дисциплине численные методыСтудента группы 19-ХТНекрасова ВладиславаЛабораторная работа №1Численные методы решения нелинейных уравнений Цель: обучение решению нелинейных уравнений численными методами.Задание.

1. 
   Отделить корни уравнения графически и уточнить один из них с точностью до 0,001
   

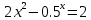
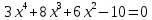
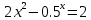
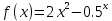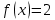
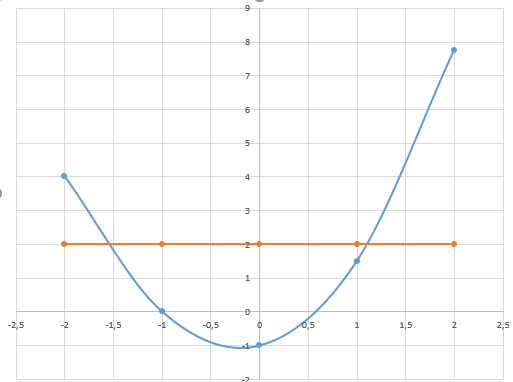
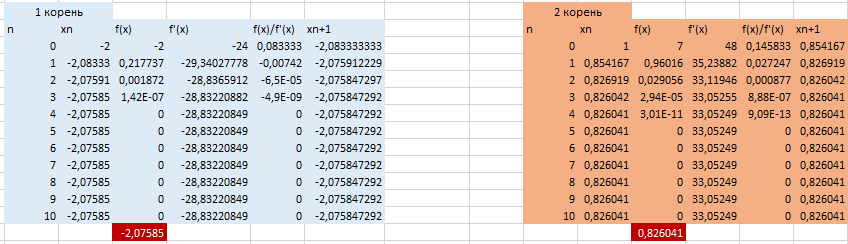
а) методом касательных (метод Ньютона);б) методом половинного уравнения.Сделайте выводы.1. 2. РешениеА) Записываем данное уравнение, в виде И строим график функций , Таким образом, корни уравнения принадлежат отрезкам [-2;-1,5], [1;1,3].Строим таблицыПервый столбец – порядковый номер;Второй столбец – значения x;Третий столбец – значение функции при заданном значении x;Четвертый столбец – значение производной данной функции при заданном значении x;Пятый столбец – отношение 3 и 4 столбцов;Шестой столбец – разность между 2 и 5 столбцами.Полученное значение x подставляем в остальные столбцы:

2. 
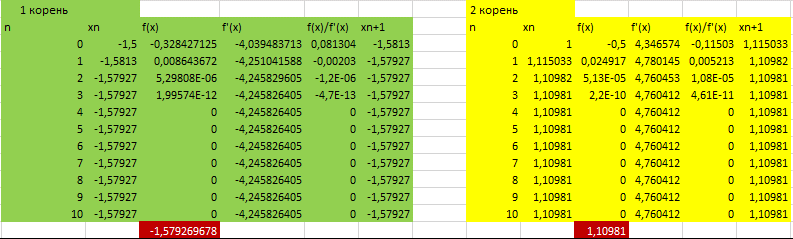
   Записываем данное уравнение, в виде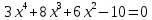
   

И строим график функций ,

---

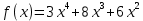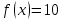
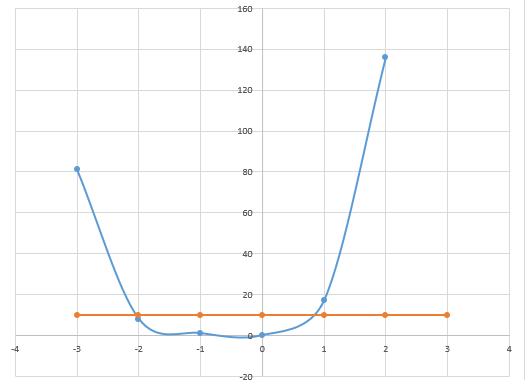
Таким образом, корни уравнения принадлежат отрезкам [-2;1,5], [1;15]Строим таблицуПервый столбец – порядковый номер;Второй столбец – значения x;Третий столбец – значение функции при заданном значении x;Четвертый столбец – значение производной данной функции при заданном значении x;Пятый столбец – отношение 3 и 4 столбцов;Шестой столбец – разность между 2 и 5 столбцами.Полученное значение x подставляем в остальные столбцы:Достоинства метода:

• 
  Быстрая сходимость
  

Недостатки метода:

• 
  Локальная сходимость (начальное приближение должно быть достаточно близко к х)
  
• 
  Жесткие требования на саму функцию (должна быть дважды непрерывно дифференцировано)
  

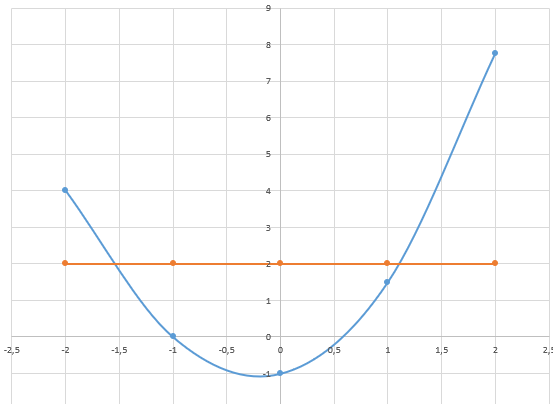
Б) Записываем данное уравнение, в виде и строим график функции Таким образом, корни уравнения принадлежат отрезкам [-2;-1,5] [1;1,3]Строим таблицуСтроим a и b – соответственно начало и конец отрезка ;Столбец с – среднее значение отрезка ;Столбец f(a) – значение функции при x=a;Столбец f(b) – значение функции при x=b;Столбец f(c) – значение функции при x=c;Далее в столбце а во второй ячейки задаем функцию Если Далее в столбце b во второй ячейки задаем функцию Если Получаем значение и растягиваем строку до конца(растягиваем таблицу вниз, пока не увидим одинаковые значения.):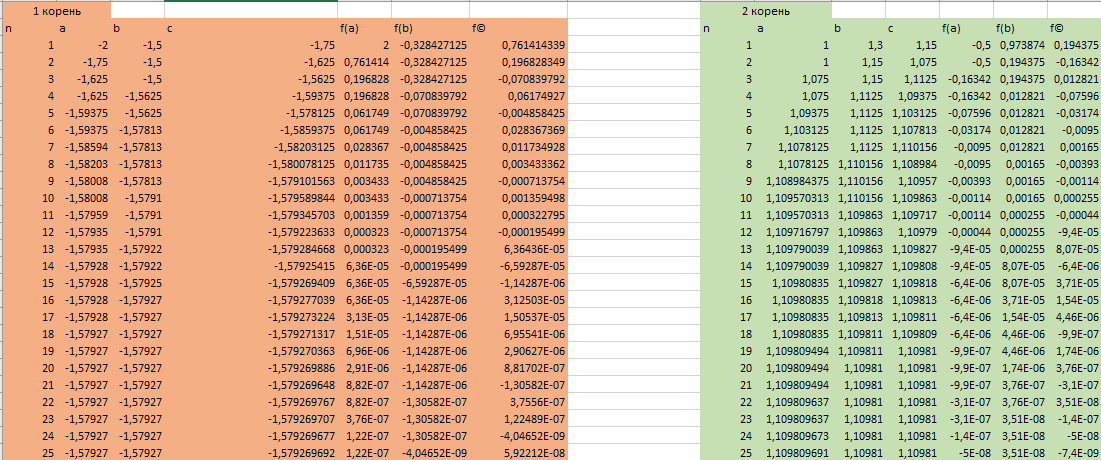2) Записываем данное уравнение, в виде и строим график функции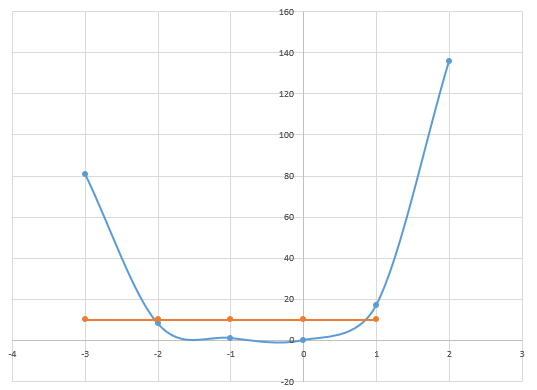Таким образом, корни уравнения принадлежат отрезкам [-2,5;-2] [0,5:1]Строим таблицу

---

Строим a и b – соответственно начало и конец отрезка ;Столбец с – среднее значение отрезка ;Столбец f(a) – значение функции при x=a;Столбец f(b) – значение функции при x=b;Столбец f(c) – значение функции при x=c;Далее в столбце а во второй ячейки задаем функцию Если Далее в столбце b во второй ячейки задаем функцию Если Далее растягиваем таблицу вниз, пока не увидим одинаковые значения:Достоинства метода:

• 
  Простота
  
• 
  Не имеет ограничений
  

Недостатки метода:

• 
  Метод неприменим к корням четной кратности
  
• 
  Скорость сходимости метода невелика
  
• 
  Метод половинного деления требует отделения корня, и для достижения высокой точности приходится вычислять функцию много раз
  

---

Смотрите также файлы

• Практическое задание 3, Модуль Особенности психического развития от юности до пожилого возраста слушатель Рублева Светлана Олеговна Преподаватель Коломейцева Лидия Владимировна.docx

• Лабораторная работа 1 Проверка основного закона динамики поступательного движения.docx

• Отчет о производственной ( технологической ) практике место практики.doc

• Расчет времени эвакуации при пожаре.docx

• Контрольная работа на тему Этические принципы работы психолога по учебной дисциплине.docx