ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 58
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| 15,8 | 19,5 | 8,9 | 17,6 | 15,4 | 21,8 | 11,3 | 25,9 | 19,1 | 16,0 |
| 11,9 | 17,0 | 25,8 | 13,1 | 25,4 | 19,0 | 22,0 | 14,9 | 26,9 | 15,1 |
| 17,7 | 19,3 | 14,8 | 22,1 | 16,4 | 29,2 | 12,5 | 19,7 | 9,0 | 17,8 |
| 11,2 | 24,8 | 13,8 | 17,9 | 17,5 | 6,7 | 22,2 | 16,2 | 18,2 | 10,9 |
| 16,1 | 17,1 | 9,5 | 22,3 | 14,6 | 19,9 | 22,4 | 17,2 | 20,3 | 12,5 |
| 12,8 | 20,4 | 18,3 | 16,9 | 18,1 | 12,2 | 20,5 | 10,7 | 17,4 | 18,8 |
| 18,0 | 6,9 | 20,7 | 12,9 | 22,7 | 27,5 | 14,1 | 20,8 | 23,0 | 21,5 |
| 13,4 | 18,4 | 17,3 | 23,1 | 18,6 | 14,0 | 24,6 | 7,3 | 23,3 | 18,5 |
| 10,2 | 21,3 | 16,6 | 28,4 | 11,6 | 23,4 | 14,4 | 28,9 | 20,9 | 29,0 |
| 18,7 | 14,3 | 21,1 | 8,4 | 19,1 | 24,4 | 21,0 | 17,5 | 26,0 | 16,8 |
Требуется:
1. Представить выборку в виде статистического ряда. Построить гистограмму и полигон частот.
2. Определить моду, медиану.
3. Определить несмещённые точечные оценки для математического ожидания, дисперсии, среднеквадратического отклонения.
4. Найти доверительный интервал для математического ожидания.
5. Приняв в качестве нулевой гипотезу H0: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить её, пользуясь критерием Пирсона при уровне значимости α = 0,025.
Решение:
1. Представим выборку в виде статистического ряда. Построим гистограмму и полигон частот.
число групп определяется по формуле Стэрджесса:
n = 1 + 3,322log n = 1 + 3,322log(100) = 8
Ширина интервала составит:
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
Аналитическая группировка.
| Группы | Кол-во, nj |
| 6.7 - 9.7 | 7 |
| 9.7 - 12.7 | 10 |
| 12.7 - 15.7 | 14 |
| 15.7 - 18.7 | 26 |
| 18.7 - 21.7 | 19 |
| 21.7 - 24.7 | 13 |
| 24.7 - 27.7 | 7 |
| 27.7 - 30.7 | 4 |
| Итого | 100 |
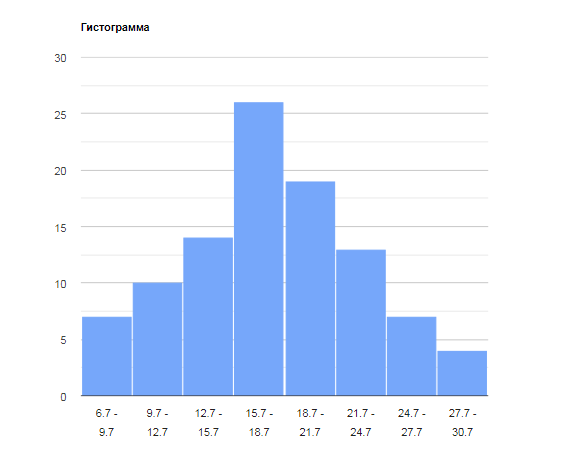
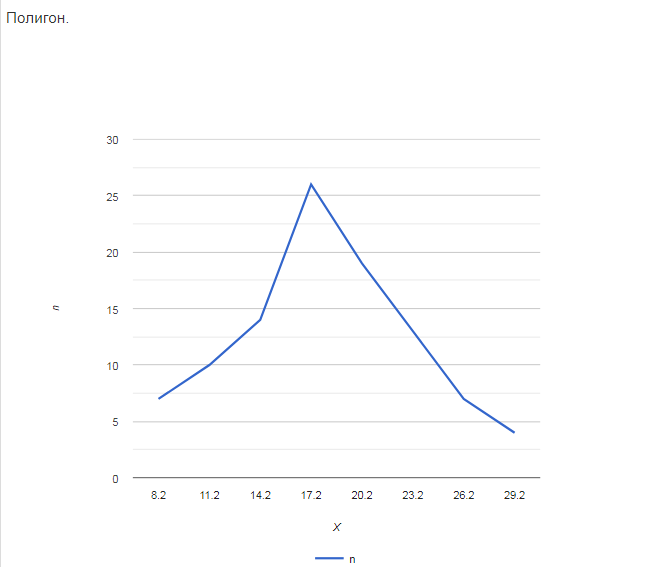
Таблица для расчета показателей.
| Группы | Середина интервала, xцентр | Кол-во, ni | xi·ni | (x-xср)2·ni | Относительная частота, ni/n |
| 6.7 - 9.7 | 8.2 | 7 | 57.4 | 673.653 | 0.07 |
| 9.7 - 12.7 | 11.2 | 10 | 112 | 463.761 | 0.1 |
| 12.7 - 15.7 | 14.2 | 14 | 198.8 | 203.225 | 0.14 |
| 15.7 - 18.7 | 17.2 | 26 | 447.2 | 17.059 | 0.26 |
| 18.7 - 21.7 | 20.2 | 19 | 383.8 | 91.126 | 0.19 |
| 21.7 - 24.7 | 23.2 | 13 | 301.6 | 350.169 | 0.13 |
| 24.7 - 27.7 | 26.2 | 7 | 183.4 | 469.533 | 0.07 |
| 27.7 - 30.7 | 29.2 | 4 | 116.8 | 500.864 | 0.04 |
| Итого | | 100 | 1801 | 2769.39 | 1 |
2. Определим моду, медиану.
Мода.
Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.
где x0 – начало модального интервала; h – величина интервала; n2 –частота, соответствующая модальному интервалу; n1 – предмодальная частота; n3 – послемодальная частота.
Выбираем в качестве начала интервала 15.7, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 17.595
Медиана.
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше.
Медиана служит хорошей характеристикой при ассиметричном распределении данных, т.к. даже при наличии "выбросов" данных, медиана более устойчива к воздействию отклоняющихся данных.
В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 15.7 - 18.7, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
Таким образом, 50% единиц совокупности будут меньше по величине 17.892.
3. Определим несмещённые точечные оценки для математического ожидания, дисперсии, среднеквадратического отклонения.
Средняя взвешенная (выборочная средняя)
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия).
Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 18.01 в среднем на 5.262
Оценка среднеквадратического отклонения.
4. Найдем доверительный интервал для математического ожидания.
Определяем значение tkp по таблице распределения Стьюдента.
По таблице Стьюдента находим:
Tтабл(n-1;α/2) = Tтабл(99;0.025) = 2.276
Стандартная ошибка выборки для среднего:
Стандартная ошибка среднего указывает, на сколько среднее выборки 18.01 отличается от среднего генеральной совокупности.
Предельная ошибка выборки:
или
ε = tkp sc = 2.276*0.529 = 1.204
Доверительный интервал: (18.01 - 1.204;18.01 + 1.204) = (16.806;19.214)
С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
5. Приняв в качестве нулевой гипотезу H0: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверим её, пользуясь критерием Пирсона при уровне значимости α = 0,025.
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону. Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа