Файл: Учебник для вузов. М Издво мгту им. Баумана, 2002, 336 с. Теоретические основы сапр Учебник для вузов Корячко В. П., Корейчик В. М., Норенков И. П. М. Энергоатомиздат, 1987, 400 с.doc
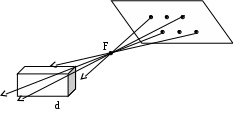
Система уравнений, описывающих эту задачу, может: вообще не иметь решений (луч проходит около поверхности); иметь единственное решение (луч пересекает плоскость или касается выпуклой поверхности), иметь несколько решений (луч пересекает кривую поверхность несколько раз) и бесконечное множество решений (луч совпадает с поверхностью). Последняя группа решений исключается из рассмотрения из-за неопределенности положения точки пересечения. В результате определения пересечения светового луча с примитивом устанавливается сам факт наличия пересечения и вычисляются координаты двух точек пересечения. Одновременно запоминаются номера поверхностей внутри описания примитива, которым эти точки принадлежат.После того как задача определения точек пересечений решена для всех примитивов, входящих в состав объекта, путем преобразования матрицы координат точек пересечения и матрицы номеров поверхностей, которым принадлежат эти точки, среди всей этой совокупности точек выделяется точка, ближайшая к наблюдателю, т.е. видимая.Формально ближайшая точка может не принадлежать поверхности объекта, как это бывает для ближних к наблюдателю вычитающихся примитивов, поэтому после выделения ближайшей точки следует убедиться в том, что она принадлежит поверхности объекта. Для этого сначала с помощью функции принадлежности оценивается положение точки по отношению к каждому примитиву, входящему в состав объекта, а затем по формальным правилам и табл. 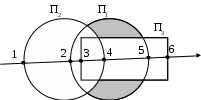1 устанавливается относительное положение точки и объекта.Например, пусть объект составлен из примитивов О = (П1 – П2) – П3. Световой луч пересекает эту комбинацию в точках 1 – 6. Ближайшей к источнику луча (т.е. к экрану) будет точка 1. Функции принадлежности этой точки и примитивов принимают значения: (X1, Y1, Z1; П1) = –1, (X1, Y1, Z1; П2) = 0, (X1, Y1, Z1; П3) = –1, тогда (X1, Y1, Z1; П1 – П2) = –1, (X1, Y1, Z1; (П1 – П2) – П3) = –1. Следовательно, точка 1, будучи ближайшей к источнику луча
, не является видимой, так как находится вне объекта. Подобным образом анализируются остальные точки и так до исчерпания всех точек. Таким образом, либо констатируется факт непересечения луча и объекта, либо определяются координаты видимой точки.
Множество точек объекта, видимых множеством рецепторов, качественно различается между собой. Одни точки освещаются прямыми лучами света, другие – находятся в тени. Алгоритм вычисления освещенности для этих групп точек существенно отличается, поэтому сначала следует установить признак освещенности – затененности для каждой видимой точки. Видимая точка находится "на свету", если она не загораживается от источника другими поверхностями, т.е. является ближайшей к источнику света среди всех остальных, лежащих на световом луче.
При изменении ракурса и положения источника света координаты видимых точек не меняются, изменяется лишь их затененность-освещенность.
