Файл: Мбоу Николаевская сош Карточки для подготовки к егэ по математике.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 51
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
В треугольнике
 5,
5,  . Найдите
. Найдите  .
. -
Боковая сторона равнобедренного треугольника равна 130, а основание равно 240. Найдите площадь этого треугольника. -
П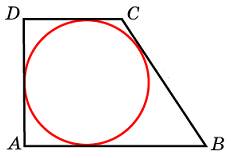
 ериметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 48. Найдите радиус окружности.
ериметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 48. Найдите радиус окружности.
-
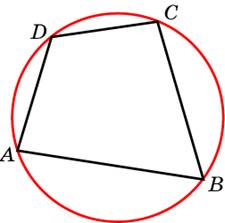
Два угла вписанного в окружность четырехугольника равны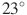 и
и 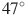 . Найдите больший из оставшихся углов. Ответ дайте в градусах.
. Найдите больший из оставшихся углов. Ответ дайте в градусах.

-
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно ,
,  ,
, 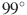 ,
, 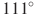 . Найдите угол B этого четырехугольника. Ответ дайте в градусах.
. Найдите угол B этого четырехугольника. Ответ дайте в градусах.
Карточка № 8
-
В треугольнике
 5,
5,  . Найдите
. Найдите  .
. -
Площадь прямоугольного треугольника равна 66. Один из его катетов на 1 больше другого. Найдите меньший катет. -
В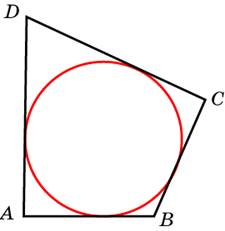 четырёхугольник
четырёхугольник  вписана окружность,
вписана окружность, 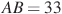 ,
,  . Найдите периметр четырёхугольника
. Найдите периметр четырёхугольника  .
.
-
Периметр правильного шестиугольника равен 180. Найдите диаметр описанной окружности.
-
У гол A четырехугольника ABCD, вписанного в окружность, равен
гол A четырехугольника ABCD, вписанного в окружность, равен 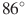 . Найдите угол C этого четырехугольника. Ответ дайте в градусах.
. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
К
 арточка № 9
арточка № 9-
В треугольнике ABC ,
,  6,
6, 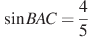 . Найдите высоту AH.
. Найдите высоту AH.
-
Основания трапеции равны 2 и 14, боковая сторона, равная 1, образует с одним из оснований трапеции угол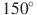 . Найдите площадь трапеции.
. Найдите площадь трапеции. -
Периметр треугольника равен 4, а радиус вписанной окружности равен 0,5. Найдите площадь этого треугольника. -
У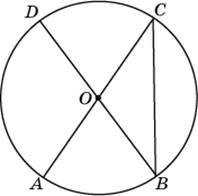 гол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен
гол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен  . Найдите число вершин многоугольника.
. Найдите число вершин многоугольника. -
Отрезки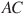 и
и 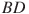 — диаметры окружности с центром
— диаметры окружности с центром  . Угол
. Угол 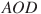 равен
равен  . Найдите вписанный угол
. Найдите вписанный угол 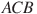 . Ответ дайте в градусах.
. Ответ дайте в градусах.
Карточка № 10
-
В треугольнике ABC ,
, 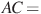 6,
6, 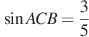 . Найдите высоту CH.
. Найдите высоту CH.
-
Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

|
К
 арточка № 11
арточка № 11-
Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.
-
Основания равнобедренной трапеции равны 9 и 15, а ее площадь равна 48. Найдите периметр трапеции. -
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен . Найдите боковую сторону треугольника, если его площадь равна 49.
. Найдите боковую сторону треугольника, если его площадь равна 49. -
В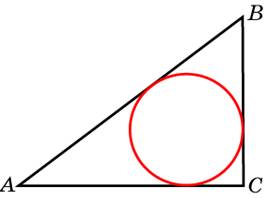 треугольнике ABC
треугольнике ABC 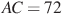 ,
, 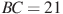 , угол C равен
, угол C равен  . Найдите радиус вписанной окружности.
. Найдите радиус вписанной окружности.
-
Дуга окружности , не содержащая точки
, не содержащая точки  , имеет градусную меру
, имеет градусную меру 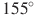 , а дуга окружности
, а дуга окружности 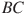 , не содержащая точки
, не содержащая точки  , имеет градусную меру
, имеет градусную меру  . Найдите вписанный угол
. Найдите вписанный угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
Карточка № 12
-
В треугольнике ABC угол C равен , CH — высота,
, CH — высота, 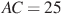 ,
, 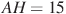 . Найдите
. Найдите .
. -
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 10 и 26. -
В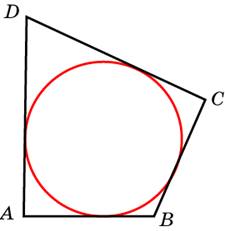 четырёхугольник
четырёхугольник  , периметр которого равен 52, вписана окружность,
, периметр которого равен 52, вписана окружность,  . Найдите
. Найдите  .
.
-
Б оковые стороны равнобедренного треугольника равны 436, основание равно 728. Найдите радиус вписанной окружности.
оковые стороны равнобедренного треугольника равны 436, основание равно 728. Найдите радиус вписанной окружности.
-
Найдите вписанный угол, опирающийся на дугу, длина которой равна длины окружности. Ответ дайте в градусах.
длины окружности. Ответ дайте в градусах.
Карточка № 13
-
В треугольнике ABC угол C равен
треугольнике ABC угол C равен  , CH — высота,
, CH — высота, 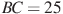 ,
, 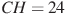 . Найдите
. Найдите .
. -
Площадь ромба равна 50. Одна из его диагоналей в 4 раза больше другой. Найдите меньшую диагональ. -
В четырехугольник ABCD вписана окружность,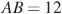 ,
, 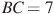 и
и  . Найдите четвертую сторону четырехугольника.
. Найдите четвертую сторону четырехугольника.
-
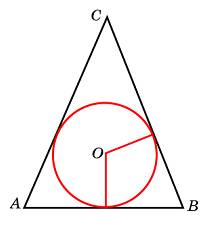
О кружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 21 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
кружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 21 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
-
Найдите хорду, на которую опирается угол , вписанный в окружность радиуса
, вписанный в окружность радиуса  .
.
 треугольнике со сторонами 7 и 14 проведены высоты к этим сторонам. Высота, проведённая к первой из этих сторон, равна 2. Чему равна высота, проведённая ко второй стороне?
треугольнике со сторонами 7 и 14 проведены высоты к этим сторонам. Высота, проведённая к первой из этих сторон, равна 2. Чему равна высота, проведённая ко второй стороне?