Файл: Умноженной на множитель в форме показательной функции W.docx

6) Понятие о нормированной частоте и основном диапазоне частот

В цифровой обработке сигналов (DSP) нормализованная частота (f ^') представляет собой величину, имеющую размерность частоты, выраженную в единицах "циклов на выборку". Она равна f ^' = f / f _s, где f - обычная частота (в "циклах в секунду"), а f _s - частота дискретизации (в "выборках в секунду"). (википедия)

Согласно т. Котельникова, верхняя частота fв аналогового сигнала не должна превышать половины частоты дискретизации fа этого сигнала. Следовательно, дискретные сигналы целесообразно рассматривать в области [0; fa/2], которая называется основной полосой частот или основным диапазоном частот.


Обычно предпочтение отдается абсолютной частоте f и нормированное частоте Ꞷ.

Например, дискретная косинусоида в области нормированных частот имеет вид

Введение нормированной частоты указывает на то, что в ЦОС важны не абсолютные значения частот сигнала и дискретизации, а их отношение. Простейшее пример двух дискретных косинусоид:

2. Прямое Z – преобразование, определение. Область сходимости, определение, примеры. Свойства (линейность, z-преобразование задержанной копии последовательности, z-преобразование последовательности x(n), умноженной на множитель в форме показательной функции Wⁿ, z-преобразование свертки двух последовательностей).

1. 
   Z – преобразование
   

Z-преобразованием (преобразованием Лорана) называют свёртывание исходного сигнала, заданного последовательностью вещественных чисел во временно́й области, в аналитическую функцию комплексной частоты. (Википедия на всякий случай, даже менять не буду, из учебника ниже)

---

При исследовании дискретных сигналов и линейных систем, как правило,

вместо дискретного преобразования Лапласа используют z преобразование, которое получается из дискретного преобразования Лапласa в результате замены переменных



z-преобразованием последовательности х(nТ) (2.16) называется следующий ряд:





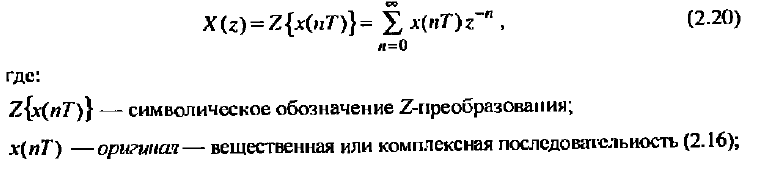
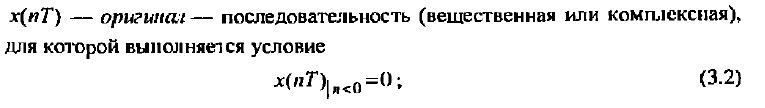
Анализ и синтез линейных дискретных систем существенно

упрощается при переходе из временной области в г-область. В частности,

z-преобразование позволяет ввести понятие передаточной функции в дробно-

рациональном виде и описать соотношение вход-выход в виде алгебраиче-

ских, а не разностных уравнений.

Х(z) — z-изображение (z-образ) последовательности х(nТ), результат

Z-преобразования.

2. 
   Область сходимости
   

Область сходимости представляет из себя некоторое множество точек на комплексной плоскости, в которых выполнено условие см ф. 2.21 ниже. То есть сумма по членам преобразования является конечной. (Википедия)

Z-преобразование однозначно связывает последовательность x(nT) с ее z-изображением Х(z) и справедливо только в области абсолютной сходимости ряда (2.20):



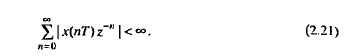
которую называют областью сходимости z-изображения.

В области сходимости ряда (2.21) обеспечивается и сходимость ряда (2.20), однако обратное не всегда справедливо. Может случиться, что ряд (2.20) сходится за счет сбалансированности слагаемых с положительными и отрицательными знаками, а ряд (2.21) расходится.







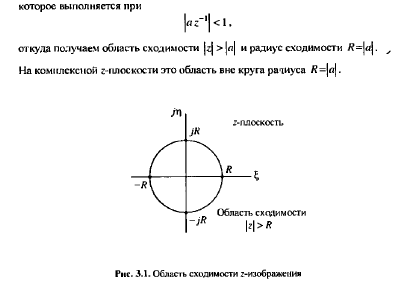
Надеюсь это идет как пример ..

3) Свойства

1. Линейность.

Если последовательность х(иТ) (3.2) равна линейной комбинации последовательностей

---

то ее z-изображение равно линейной комбинации z-изображений данных

последовательностей:





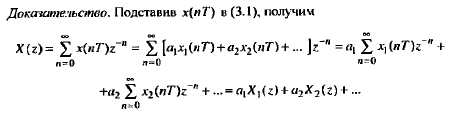
2. Z-преобразование задержанной последовательности (теорема о задержке).

Z-изображение последовательности x[(n-m)T]. задержанной на (m>0) отсчетов, равно z- изображению незадержанной последовательности x(nT), умноженному на z^-m :







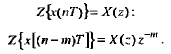
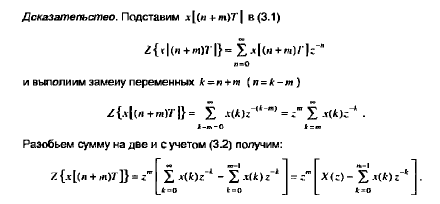
3. Z-преобразование свертки последовательностей (теорема о свертке).

Сверткой последовательностей х1(nТ) и х2(nТ) называется последовательность x(nТ), определяемая соотношением:



Z-изображение свертки равно произведению z-изображений свертываемых последовательностей:

3. Математическая модель АЦП как идеального амплитудно-импульсного модулятора. Математическая модель дискредитированного во времени сигнала. Преобразование Лапласа и Фурье дискретизированного во времени сигнала. Интервал/период дискретизации, частота и угловая частота дискретизации.

Математическая модель АЦП как идеального амплитудно-импульсного модулятора.

Математическая модель АЦП

Математическую модель АЦП можно представить в виде следующей структурной схемы, изображенной на рисунке 11

---

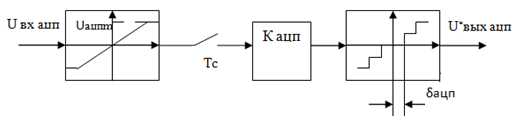
Рисунок 11 - Структурная схема АЦП

На рисунке 11 имеются обозначения:

U_{вх ацп} - максимальное входное напряжение АЦП, В;

К_ацп - крутизна АЦП,

д_ацп - величина единицы младшего разряда.

Рассчитаем параметры математической модели АЦП.

Величина младшего разряда АЦП

 

Крутизна АЦП



,

где U_{вх ацп} - максимальное входное напряжение АЦП,В;

n_ацп - число разрядов АЦП.



К_ацп = = 0,02 рад/В

Математическая модель дискредитированного во времени сигнала.

Математическая модель дискретизации сигналов во временной области

            Процесс получения  отсчетов (sampling) или дискретизации сигнала можно рассматривать как умножение сигнала аналогового  сигнала  x_a(t) на периодическую последовательность p(t) тактовых импульсов единичной амплитуды и длительностью  τ, много меньшей периода отсчетов  T_S =T= 1 / F_s.  Умножение двух сигналов – это модуляция одного сигнала другим. Поэтому процесс дискретизации можно рассматривать как амплитудно-импульсную модуляцию (АИМ).

 



 

 

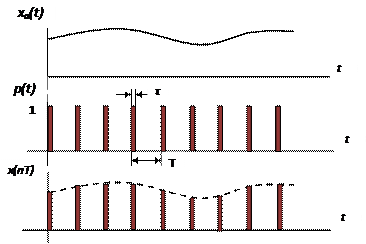
Отсчеты аналогового сигнала в равноотстоящие моменты времениt = nT   образуют последовательность x[n] = x_a(nT).    

Поскольку   τ<<T, то в идеальной модели дискретизации импульсная последовательность  p(t)  представляется как периодическая последовательность  δ – функций.

---

 

     

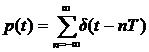
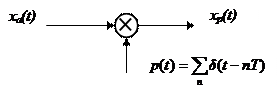
Процесс получения отсчетов (sampling) – это умножение непрерывного сигнала  x_a(t) на периодическую последовательность  импульсов (periodic impulse train)  p(t).  Происходит  изменение амплитуды последовательности p(t) по закону аналогового сигнала  , т.е.   амплитудно – импульсная модуляция   (АИМ)  последовательности.

Результирующая последовательность  x_p(t)  представляет собой периодическую с периодом   T последовательность δ – функций с площадями, равными значениям  x_a(nT): 

 

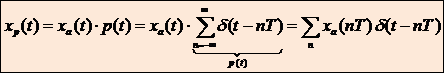
Полученное выше выражение позволяет выразить дискретный сигнал через       δ – функции как функцию непрерывного времениt.

Реальный дискретный сигнал отличается от идеального хотя и малой, но конечной длительностью каждого отсчета. Это связано с конечным быстродействием устройства выборки  и хранения (УВХ) АЦП.  Для получения такого сигнала идеальный дискретный сигнал x_p(t) свертывается (операция свертки!) с реальным тактовым импульсом  r(t)



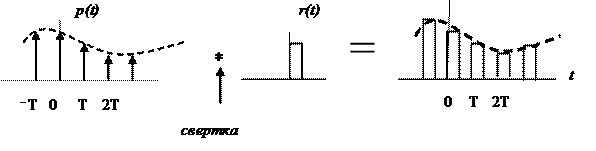
В результате свертки реальный (не идеальный) дискретный сигнал во временной области имеет вид



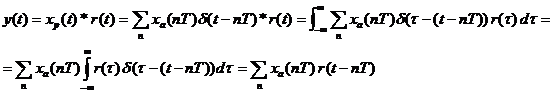
При этом r(t) – форма сигнала несущей импульсной последовательности.

 Результат – последовательность отсчетов – импульсов   с конечной длительностью.

Преобразование Лапласа и Фурье дискретизированного во времени сигнала.

Формула Фурье для дискретного сигнала:

 – прямое преобразование Фурье.

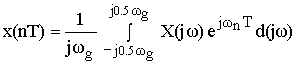 – обратное преобразование Фурье.

Сигнал x(nT) нормирован по отношению к X. 

После денормирования сигнала формулу записываем в виде:

---