Конспект урока

Информатика, 10 класс. Урок № 13.

Тема — Логические задачи и способы их решения

Перечень вопросов, рассматриваемых в теме: метод рассуждений, табличный метод, метод упрощения логических выражений.

Глоссарий по теме: для решения логических задач необходимо знать таблицы истинности логических операций и правила преобразования логических выражений (законы алгебры логики). Этот материал рассмотрен в предыдущих уроках №11,12.

Основная литература по теме урока:

Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса

— М.: БИНОМ. Лаборатория знаний, 2017 (с.197—209)

Открытые электронные ресурсы по теме:

http://lbz.ru/metodist/authors/informatika/3/eor10.php

http://kpolyakov.spb.ru/school/ege.htm

Теоретический материал для самостоятельного изучения

Исходными данными в логических задачах являются высказывания. Высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов сложно. Способов решения логических задач немало, но наибольшее распространение получили метод рассуждений, табличный метод и метод упрощения логических выражений. Познакомимся с ними поочередно.

Метод рассуждений

Основная идея этого метода состоит в том, чтобы последовательно анализировать всю информацию, имеющуюся в задаче, и делать на этой основе выводы.

Пример 1. На одной улице стоят в ряд 4 дома, в каждом из которых живёт по одному человеку. Их зовут Василий, Семён, Геннадий и Иван. Известно, что все они имеют разные профессии: скрипач, столяр, охотник и врач. Известно, что:

— столяр живёт правее охотника;

— врач живёт левее охотника;

— скрипач живёт с краю;

— скрипач живёт рядом с врачом;

— Семён не скрипач и не живёт рядом со скрипачом;

— Иван живёт рядом с охотником;

— Василий живёт правее врача;

— Василий живёт через дом от Ивана.

Определим, кто где живёт.

Изобразим дома прямоугольниками и пронумеруем их:

---

Известно, что скрипач живёт с краю (3). Следовательно, он может жить в доме 1 или в доме 4.



Скрипач живёт рядом с врачом (4), т. е. врач может жить правее (дом 2) или левее (дом 3) скрипача.



Но врач живёт левее охотника (2), следовательно, скрипач не может жить в доме 4, т. к. в противном случае получится, что врач, живущий рядом с ним, живёт правее охотника, а это противоречит условию (2). Таким образом, скрипач живёт в доме 1, а врач — рядом с ним, в доме 2.



Так как врач живёт левее охотника (2), а столяр — правее охотника (1), то охотнику достается дом 3, а столяру — дом 4.



Так как Семён не скрипач и не живёт рядом со скрипачом (5), то он может жить в доме 3 или в доме 4.



Так как Иван живёт рядом с охотником (6), то он может жить в доме 2 или 4.



Так как Василий живёт правее врача (7), то он может жить в доме 3 или 4.



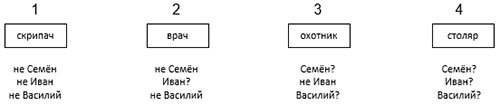
По условию (8) Василий живет через дом от Ивана, значит, в доме 1 может жить только Геннадий, в доме 2 — Иван, в доме 4 — Василий, в доме 3 — Семён.



Как видите, далеко не самая сложна задача потребовала достаточно серьезных рассуждений. Этот метод, как правило, применяется для решения простых задач.

Задачи о рыцарях и лжецах — это такой класс логических задач, в которых фигурируют персонажи:

- рыцарь — человек, всегда говорящий правду;

- лжец — человек, всегда говорящий ложь;

- обычный человек — человек, который в одних ситуациях может говорить правду, а в других лгать.

---

Решение подобных задач сводится к перебору вариантов и исключению тех из них, которые противоречат условию.

Пример 2.Двое жителей острова А и В разговаривали между собой в саду. Проходивший мимо незнакомец спросил у А: «Вы рыцарь или лжец?». Тот ответил, но так неразборчиво, что незнакомец не смог ничего понять. Тогда незнакомец спросил у В: «Что сказал А?».

«А сказал, что он лжец», — ответил В. Может ли незнакомец доверять ответу В? Мог ли А сказать, что он лжец?

Если А — рыцарь, то он скажет правду и сообщит, что он рыцарь.

Если А — лжец, то он скроет правду и сообщит, что он рыцарь.

Это значит, что В, утверждающий, что «А сказал, что он лжец» заведомо лжёт; он – лжец.

Определить, кем является А, в данной ситуации невозможно.

Табличный метод

Для решения логических задач, связанных с рассмотрением нескольких конечных множеств, прибегают к помощи таблиц или графов. От того, насколько удачно выбрана их структура, во многом зависит успешность решения задачи.

Пример 3. В летнем лагере в одной палатке жили Алёша, Боря, Витя и Гриша. Все они разного возраста, учатся в разных классах (с 7-го по 10-й) и занимаются в разных кружках: математическом, авиамодельном, шахматном и фотокружке. Выяснилось, что

— фотограф старше Гриши;

— Алеша старше Вити, а шахматист старше Алёши;

— в воскресенье Алёша с фотографом играли в теннис, а Гриша в то же время проиграл авиамоделисту в городки.

Определим, кто в каком кружке занимается.

В этой задаче речь идёт о высказывательной форме (предикате) вида «Ученик х занимается в кружке у». Требуется определить такие значения х и у, чтобы высказывательная форма превратилась в истинное высказывание.

Составим таблицу:



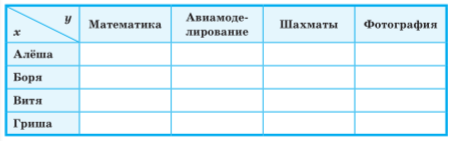
Рассмотрим условия (1)-(3) и сделаем выводы: Гриша — не фотограф (1); шахматист — не Алёша и не Витя (2); Алёша — не фотограф и не авиамоделист, Гриша — не фотограф и не авиамоделист (3). Отметим это в таблице:



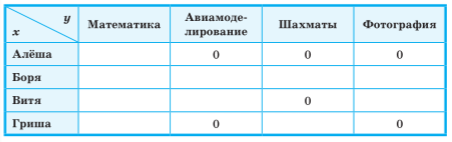
Мы можем сделать вывод, что Алёша занимается математикой

---

, а Гриша — шахматами:



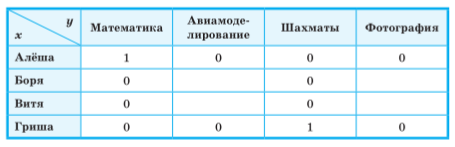
Из того, что Гриша — шахматист и условий (1) и (2) можем расположить учеников по возрасту (в порядке возрастания): Витя — Алёша — Гриша — фотограф. Следовательно, Боря — фотограф.



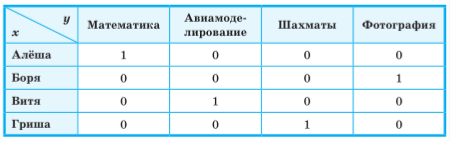
Ответ: Витя (7 класс) занимается в авиамодельном кружке, Алёша (8 класс) — в математическом, Гриша (9 класс) — в шахматном, Боря (10 класс) — в фотокружке.

Использование таблиц истинности для решения логических задач

Аппарат алгебры логики позволяет применять к широкому классу логических задач универсальные методы, основанные на формализации условий задачи.

Одним из таких методов является построение таблицы истинности по условию задачи и её анализ. Для этого следует:

1. 
   Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами.
   
2. 
   Записать условие задачи на языке алгебры логики, соединив простые высказывания в составные с помощью логических операций.
   
3. 
   Построить таблицу истинности для полученных логических выражений.
   
4. 
   Выбрать решение – набор логических переменных (элементарных высказываний), при котором значения логических выражений соответствуют условиям задачи.
   
5. 
   Убедиться, что полученное решение удовлетворяет условиям задачи.
   

Пример 4. Три подразделения А, В, С торговой фирмы стремились получить по итогам года максимальную прибыль. Экономисты высказали следующие предположения:

1. 
   Если А получит максимальную прибыль, то максимальную прибыль получат В и С.
   
2. 
   А и С получат или не получат максимальную прибыль одновременно.
   
3. 
   Необходимым условием получения максимальной прибыли подразделением С является получение максимальной прибыли подразделением В.
   

По завершении года оказалось, что одно из трёх предположений ложно, а остальные два истинны.

Выясним, какие из названных подразделений получили максимальную прибыль.

Рассмотрим элементарные высказывания:

А — «А получит максимальную прибыль»;

В — «В получит максимальную прибыль»;

С — «С получит максимальную прибыль».

Запишем на языке алгебры логики прогнозы, высказанные экономистами:

---

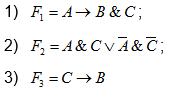
Составим таблицу истинности для F₁, F₂, F₃.



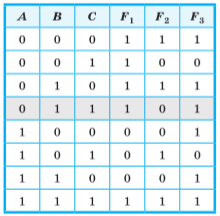
Вспомним, что из трёх прогнозов F₁, F₂, F₃ один оказался ложным, а два других — истинным. Эта ситуация соответствует четвёртой строке таблицы.

Ответ: максимальную прибыль получили подразделения В и С.

Метод упрощения логических выражений

Следующий формальный способ решения логических задач состоит в том, чтобы:

1. 
   Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами.
   
2. 
   Записать условие задачи на языке алгебры логики, соединив простые высказывания в составные с помощью логических операций.
   
3. 
   Составить единое логическое выражение, учитывающее все требования задачи.
   
4. 
   Используя законы алгебры логики, упростить полученное выражение и вычислить его значение.
   
5. 
   Выбрать решение – набор логических переменных (элементарных высказываний), при котором построенное логическое выражение является истинным.
   
6. 
   Убедиться, что полученное решение удовлетворяет условиям задачи.
   

Пример 5. На вопрос, кто из трёх учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?

Обозначим через А, В, С простые высказывания:

А — «Первыйученик изучал логику»;

В — «Второйученик изучал логику»;

С — «Третийученик изучал логику».

Из условия задачи следует истинность высказывания:  .

Упростим получившееся высказывание:



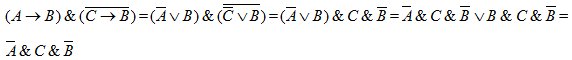
Получившееся высказывание будет истинным только в случае, если С — истина, а А и В — ложь.

Ответ: логику изучал только третий ученик.

---

Смотрите также файлы

• ндірістік педагогикалы практика бойынша студентті.docx

• Урока мы начинаем знакомство с большой и важной темой периодический закон и периодическая система д. И. Менделеева. Но это тема большого количества уроков, а о чём мы будем говорить сегодня, вы узнаете, разгадав ребус, посмотрите на доску. Классификация.docx

• Павлодар облысы Терекл ауданы Фрументьевка негізгі орта мектебіні аза тілі мен дебиеті пніні малімі Базарова Гульжан Ескалиевнаа Пікір.docx

• Новая модель семейных отношений предполагает обеспечить условия для общественнопроизводственной деятельности женщины и вернуть в семью мужчину как равноправного ее члена.docx

• Сауалнама Мені бос уаытым Атыжні Жасы нешеде.docx