Файл: Методическое пособие для курсовой работы санктпетербург 2021 содержание введение 3 общие требования 3.docx

2. Примеры использования метода PCA

Пример1.

Рассмотрим пример использования метода главных компонент для понижения размерности изображения и оценим потери визуально. Возьмем небольшой jpg файл и посмотрим, какое число главных компонент будет достаточным для представления изображения в допустимом качестве.

Будем вычислять главные компоненты используя сингулярное разложение матриц, которое выполняется с помощью функции svd, включенной в базовое программное обеспечение языка R. Эта функция вычисляет три матрицы

S, U и Vсингулярного разложения. Их мы будем использовать как основу и выбирать из них разное число главных компонент k, формируя сжатые изображения. Качество получаемых изображений будем оценивать чисто визуально.

Решение задачи выполним в среде RStudio (листинг 1). Для работы с jpg форматом воспользуемся библиотекой jpeg(строка2), позволяющей, в частности читать (функция readJPEG) и визуализировать (функция rasterImage) изображения. Для перевода цветного изображения в черно-белое используем библиотеку biOps(строка 3). В настоящее время эта библиотека исключена из репозитория CRAN и там дается только ссылка на архив, где она хранится. Прочитав архив по этой ссылке можно установить библиотеку с помощью следующей команды:
install.packages(path_to_file, repos = NULL, type="source"),
где path_to_file - путь к архивированному файлу. После чтения и перевода в черно-белое представление визуализируем оригинал изображения (строка 9, 10). Далее определяем размерность исходного изображения (dim(X) = 500 x 473) для дальнейшей оценки эффективности сжатия (строка 12). Наконец, находим сингулярное разложение X.svd(строка 14).
Листинг 1. Использование метода главных компонент для понижения размерности


В нашем случае полученное сингулярное разложение X.svd представлено в виде списка (Largelist), состоящего из трех матриц, параметры которых можно посмотреть в закладе Environment правой верхней панелиRStudioи на рис. 4.

---

Рис. 4. Сингулярное разложение X.svd
Как видно из рис. 4, диагональная матрица S имеет размер 473 х 473, матрица U размер 500 х 473 и матрица V размер 473 х 473.

Матрицы S, U и V будем использовать как основу и выбирать из них разное число главных компонент k. Сформируем различные матрицы X_k, формирование проведем в цикле (строки 22-31 листинга 1) для числа компонент k = 5, 20, 50 и 250.

Сначала сформируем усеченные матрицы Uk, Vk и Sk (строки 23-25). Затем в строке 26 выполним умножение сформированных матриц (см. рис. 2) для формирования сжатых изображений. Результатом работы этой программы будет четыре изображения, отличающихся по качеству (рис. 3):

Рис. 3. Изображения для k = 5, 20, 50, 250, соответственно
Полагаем, что допустимым качеством обладает изображение для k = 50 сингулярных значений. Посмотрим, какой выигрыш мы можем получить используя его вместо оригинала.

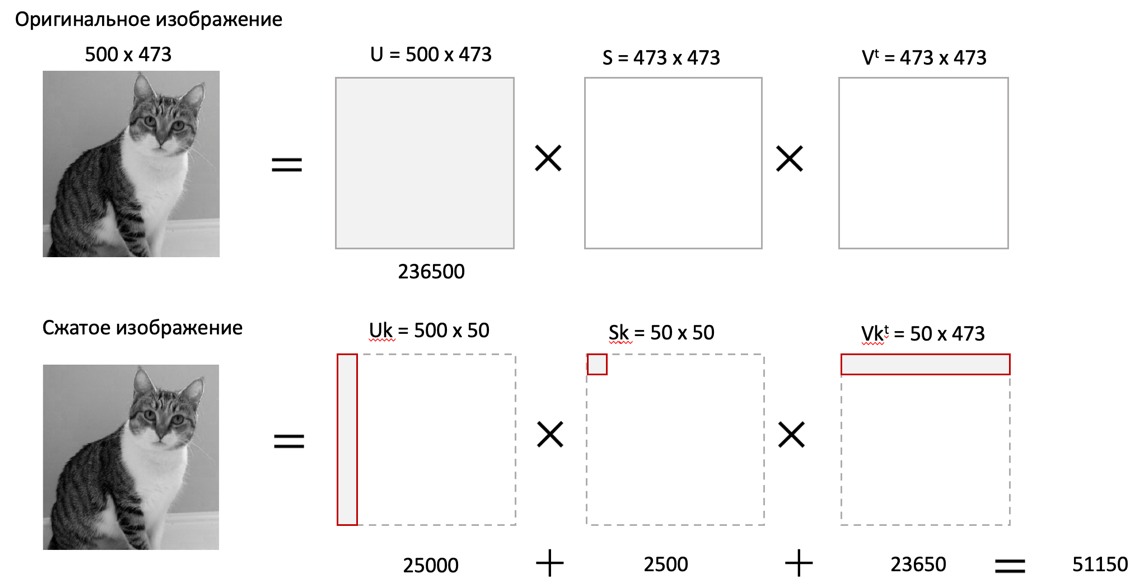
Рис. 4. Сравнение размерностей оригинального и сжатого изображения
На рис. 4 приведено такое сравнение, где показано, что вместо 236500 пикселей нам потребуется всего 51150, то есть m 4,6 раза.

Для оценки количества информации, которое мы потеряем, заменив оригинальное изображение на сжатое, можно поступить следующим образом. Если суммарное количество значений всех главных компонент принять за 100% информационного наполнения оригинала, то сумма значений k главных компонент сжатого изображения определит его информационное наполнение. Разность вычисленных таким образом величин и даст оценку «потерянной»
Пример 2.

Рассмотрим еще один пример использования метода PCA для анализа набора данных MNIST из [https://www.kaggle.com/oddrationale/mnist-in-csv]. Здесь имеется 60000 изображений рукописных цифр (mnist_train.csv) для обучения и 10000 изображений для тестирования (mnist_test.csv). Каждая цифра представлена вектором размерности 785, в котором изображение цифры занимает 28х28=784 компоненты и одна компонента label служит для идентификации изображенной цифры.

Загрузим из ресурса файл mnist_test.csvв свой рабочий директорий. Возьмем из него 6000 случайно выбранных образцов и рассмотрим как будут классифицироваться эти образцы с использованием двух главных компонент (листинг 2).

После чтения исследуемого набора в память (строка 4), определяем компоненту вектора

---

label, как фактор (строка 5). Для воспроизводимости эксперимента устанавливаем фиксированную начальную фазу генератора случайных чисел set.seed(1), перед случайным выбором 6000 образцов (строка 6). Случайно выбранные образцы записываем в матрицу train (строка 8) и вычисляем две главные компоненты с помощью функции princomp. Важно отметить, что при вычислении главных компонент данной функцией первая компонента label из матрицы образцов должна быть исключена train[,-1].
Листинг 2. Проецирование MNIST на плоскость с использованием PCA


В результате мы получим следующую визуализацию (рис. 5), которая показывает потенциальные возможности классификации набора.


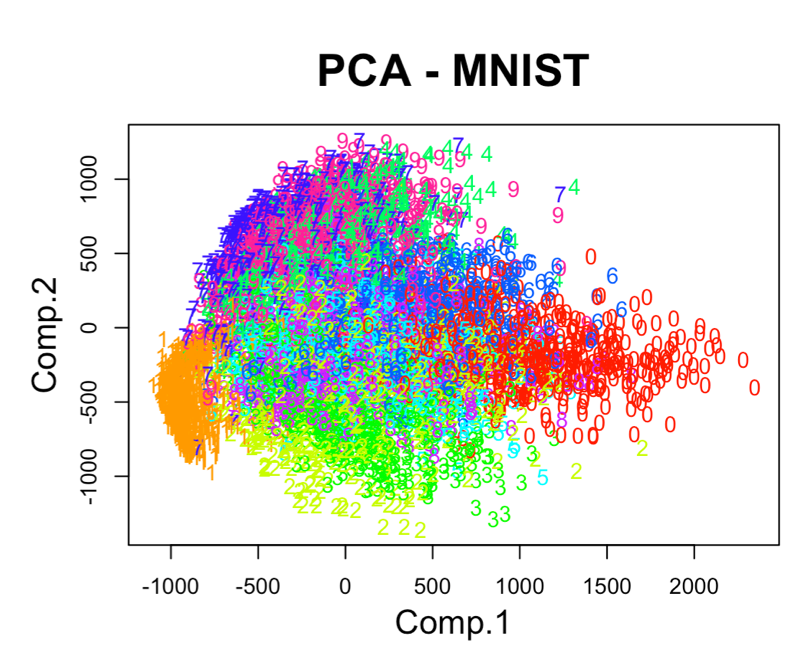
Рис. 5. Визуализация MNIST по двум главным компонентам PCA
Анализ визуализации рис. 5 не позволяет нам сделать никаких однозначных выводов о достижимой точности классификации набора MNIST.

3. Алгоритм t-SNE

t-распределенное стохастическое соседнее вложение t-SNE (t-Distributed Stochastic Neighbor Embedding) - это алгоритм нелинейного уменьшения размерности, используемый для исследования данных большой размерности. Он отображает многомерные данные в двух или более измерениях, подходящих для наблюдения человеком. Алгоритм t-SNE (2008), в ряде случаев намного эффективнее PCA (1933). Важно подчеркнуть, что большинство нелинейных методов, кроме t-SNE, не способны одновременно сохранять локальную и глобальную структуру данных [L.J.P. van der Maaten and G.E. Hinton. Visualizing High-Dimensional Data Using  t-SNE. Journal of Machine Learning Research 9(Nov):2579-2605, 2008].

SNE начинается с преобразования многомерной евклидовой дистанции между точками в условные вероятности, отражающие сходство точек. Математически это выглядит следующим образом: 

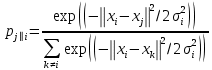
Формула показывает, насколько точка x_j близка к точке x_i при гауссовом распределении вокруг x_iс заданным отклонением σ. Сигма будет различной для каждой точки. Она выбирается так, чтобы точки в областях с большей плотностью имели меньшую дисперсию. Для этого используется оценка перплексии (perplexity):

,

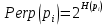где

---

- энтропия Шеннона.

Перплексия может быть интерпретирована как сглаженная оценка эффективного количества «соседей» для точки x_i. Она задается в качестве параметра метода t-SNE и рекомендуется использовать ее значение в интервале от 5 до 50. Сигма определяется для каждой пары x_i и x_j при помощи алгоритма бинарного поиска.

Таким образом, t-SNE алгоритм нелинейного уменьшения размерности, находит закономерности в данных, идентифицируя наблюдаемые кластеры на основе сходства точек данных с несколькими функциями. Но это не алгоритм кластеризации, а алгоритм уменьшения размерности, который просто отображает многомерные данные в более низкоразмерное пространство, а не идентифицирует входные объекты. Таким образом, вы не можете делать никаких выводов, основываясь только на t-SNE. По сути, это в основном техника исследования и визуализации данных. Но алгоритм t-SNE можно использовать в процессе классификации и кластеризации, используя его выходные данные в качестве входных характеристик для других алгоритмов классификации.

Алгоритм t-SNE можно использовать практически для всех многомерных наборов данных. Он особенно широко применяется в обработке изображений, естественного языка и геномных данных. 

Ниже приведены распространенные ошибки, которых следует избегать при интерпретации результатов анализа с использованием алгоритма t-SNE:

• 
  Чтобы алгоритм работал правильно перплексия должна находится в диапазоне от 5 до 50 и должна быть меньше количества переменных.
  
• 
  Размеры кластеров на любом графике t-SNE не должны оцениваться на предмет стандартного отклонения, дисперсии или любых других аналогичных показателей. Это связано с тем, что t-SNE расширяет более плотные кластеры и сжимает более разреженные кластеры для выравнивания размеров кластеров. Это одна из причин получения четких и ясных графиков.
  
• 
  Расстояния между кластерами могут измениться, потому что глобальная геометрия тесно связана с оптимальной сложностью. А в наборе данных с множеством кластеров с разным количеством элементов одна перплексия не может оптимизировать расстояния для всех кластеров.
  
• 
  Шаблоны также могут быть обнаружены в случайном шуме, поэтому необходимо проверить несколько запусков алгоритма с разными наборами гиперпараметров, прежде чем решать, существует ли шаблон в данных.
  
• 
  Различные формы кластеров могут наблюдаться на разных уровнях сложности.
  
• 
  Топология не может быть проанализирована на основе одного графика t-SNE, перед проведением какой-либо оценки необходимо наблюдать несколько графиков.
  

---

4. Примеры использования алгоритма t-SNE

Пример 1.

Рассмотрим пример использования алгоритма t-SNE для анализа набора данных MNIST и сравним его возможности с результатом полученным ранее с использованием метода РСА (листинг 3):
Листинг 3. Анализ MNIST методами PCA и t-SNE


По отношению к предыдущему листингу в листинг 3 добавлена функция Rtsne (строка 9) для реализации алгоритма t-SNE. Она имеет много входных параметров для настройки.

Для наглядности в строке 15 параметр par(mflow= c(1,2)) определяет вывод двух графиков рядом в оной строке. В результате мы получим следующую визуализацию (рис. 6).


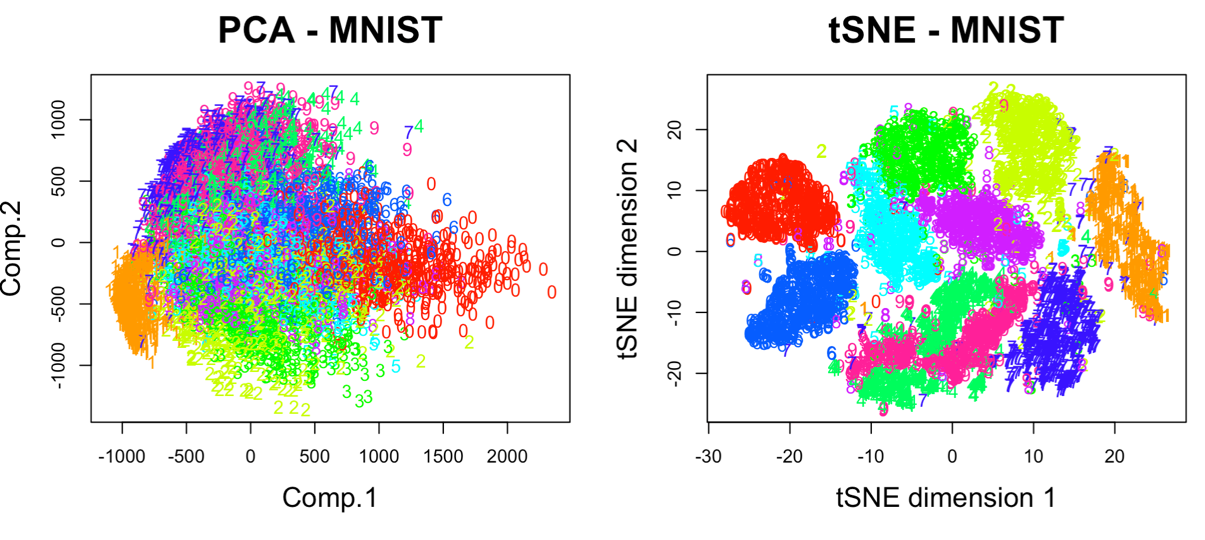
Рис. 6. Визуализация MNIST по двум компонентам с использованием PCA и tSNE
Анализ визуализации рис. 6 справа позволяет сделать вывод о достижимой точности классификации набора MNIST гораздо более оптимистичным.
Пример 2.

Рассмотрим пример исследования данных по 250000 заемщиков, представленных в [https://www.kaggle.com/c/GiveMeSomeCredit/data] и оценим эффективность их использования для кредитного скоринга. Банки играют решающую роль в рыночной экономике. Они определяют, кто может получить финансирование и на каких условиях, а также могут принимать или отменять инвестиционные решения. Для функционирования рынков и общества отдельным лицам и компаниям необходим доступ к кредитам. Алгоритмы кредитного скоринга банки используют для определения того, следует ли предоставлять ссуду. По-сути, скоринг позволяет оценить вероятности дефолта для отдельных групп заемщиков. 

Посмотрим насколько алгоритм t-SNE подходит для решения подобной задачи. Загрузим файл cs-test.csv из [] в рабочий директорий RStudio. Ниже представлен листинг использования этого алгоритма для скоринга (листинг 4).

Сначала загружаем необходимые библиотеки (строки 1-6) и читаем исследуемый файл из рабочего директория (строка 8). Затем подготавливаем загруженные данные для анализа:

• 
  удаляем неинформативные столбцы (строка 10, 11);
  
• 
  преобразуем данные в форму data.table (строка 13);
  
• 
  удаляем строки с пропущенными значениями атрибутов (строка 15).
  

В строке 18 уточняем размерность анализируемых данных после проведенных преобразований (осталось 81400 векторов для анализа). Для сокращения времени анализа возьмем только 500 случайных образцов (общая тенденция не изменится).

---