Файл: В. Ф. Пономарев математическая логика.doc

Например, формула _x(F(x))_x(F(x)) является истинной для одного элемента множества V и ложной для всех элементов этого множества, т.к.

_x(F(x))_x(F(x)):=” если существует x, для которого F(x)=и, то не для всех х универсума F(x)=и” .
2.2.2 Правила вывода

Вывод заключения из множества посылок записывается так же, как в исчислении высказываний

F₁;F₂;F_n B, где слева от знака “” записывают множество формул посылок и необходимые аксиомы F₁;F₂;F_n, а справа – формулу заключения B. Тогда знак “” означает “верно, что B выводима из F₁;F₂;F_n.

Отношение логического вывода эквивалентно теореме

F₁;F₂;F_nB.

Д ругая форма записи : F₁; F₂;F_n

B,

где над чертой записывают множество посылок и аксиом F₁;F₂;F_n, а под чертой заключение B.

Для организации вывода заключения из множества посылок используют правила подстановки и правила заключения.
2.2.2.1 Правила подстановки

Если в формулу F(х), содержащей свободную переменную x, выполнить всюду подстановку вместо x терма t , то получим формулу F(t).

Этот факт записывают так:

_x^tF(x)

F(t).
Подстановка некоторого терма t в формулу F(x) вместо ее свободной переменной x состоит в замещении всех свободных вхождений этой переменной данным термом t. Такая подстановка называется правильной. Подстановка будет неправильной если в результате подстановки сколемовской функции свободная переменная окажется в области действия квантора.

Например,

1. _x1^x2_x3( P²₁(x₁, x₃) P₂ (x₂))

_x3( P²₁(x₂, x₃) P₂ (x₂)).

Это правильная подстановка, т.к. x₁ –свободная переменная.

2 . _x1^{f(x2, t)} _x3( P²₁(x₁, x₃) P₂ (x₂))

_x3( P²₁(f(x2, t), x₃) P₂ (x₂)).

Это - правильная подстановка, т.к. x₁ –свободная переменная.




3. _x3^x2_x3( P²₁(x₁

---

, x₃) P₂ (x₂))

_x3( P²₁(x₁, x₂) P₂ (x₂)).

Э то - неправильная подстановка, т.к. x₃ –связанная квантором .

4. _x2^x3_x3( P₁(x₁, x₃) P₂ (x₂))

_x3( P₁(x₁, x₃) P₂ (x₃)).

Это - неправильная подстановка, т.к. предикат P₂ (x₃) попадает в область действия квантора .

Понятие правильной подстановки необходимо, например, для формулировки законов снятия квантора общности

_x F(x)

F(t)
и введения квантора существования

F(t)

_xF(x).

2.2.2.2 Правила введения и удаления кванторов

Наиболее распространенными правилами являются:

1) Введение квантора общности: “если F₁(t) F₂(x) выводимая формула и F₁(t) не содержит свободной переменной x , то F₁(t) x(F₂(x)) также выводима”, т.е.

(F₁(t) F₂(x))

(F₁(t) _x(F₂(x))).

2) Удаление квантора общности: "если _x(F(x)) выводимая формула, то вместо x можно выполнить подстановку терма t, свободного от x , и получить также выводимую формулу F (t), т.е.

 _x(F(x))

. F (t).

3) Введение квантора существования: "если терм t вхо­дит в предикат F(t) , то существует, по крайней мере одна предмет­ная переменная x , удовлетворяющая требованиям _x(F(x)) ”, т.е.

F(t)

_x(F(x)).

2. 
   4) Смена квантора:
   

_x(F(x)) _x(F(x))

_x(F(x)); _x(F(x)).

3. 
   5) Перенос квантора, если терм t не содержит переменной x:
   

a ) _x(F₁(x)) F₂(t)

_x(F₁(x) F₂(t));

b

---

) _x(F₁(x))F₂(t)

_x(F₁(x) F₂(t);

c ) F₁(t) _x(F₂(x))

_x(F₁(t)F₂(x));

d) _x(P(x))F(t)

_x(P(x)F(t));
e) _x(P(x))F(t)

_x(P(x)F(t)).

6) Введение новой переменной:

a ) _x(F₁(x))_x(F₂(x))

_y_x(F₁(y) F₂(x));

b ) _x(F₁(x))_x( F₂(x))

_y_x(F₁(y) F₂(x)).

2.2.2.3 Правила заключения

Существует два основных правила определения истинности заключения:

а) если F₁ и (F₁F₂) выводимые фор­мулы, то F₂ также выводима. Это - правило modus ponens (m.p).

F ₁; (F₁F₂)

F_2.

b) если F₂ и (F₁F₂) выводимые формулы, то F₁ также. выводима. Это - правило modus tollens (m.t).

F ₂; (F₁F₂)

F_1.
Эти правила определяют схему вывода и позволяют использовать правила подстановки, введения и удаления кванторов и делать вывод об истинности заключения.


2.2.3 Метод дедуктивного вывода

В логике предикатов вывод определяется так же, как в исчислении высказываний. Все правила вывода логики высказываний включены в множество правил логики предикатов.

Пример: “Таможенные чиновники обыскивают каждого, кто въезжает в страну, кроме высокопоставленных лиц. Если некоторые люди способствуют провозу наркотиков, то на внутреннем рынке есть наркотик. Никто из высокопоставленных лиц не способствовает провозу наркотиков. Следовательно, некоторые из таможников способствуют провозу наркотиков?”

Пусть P₁(x):=”x - таможенный чиновник”, P₂(x,y):=”x обыскивает y”, P₃(y):=”y въезжает в страну”, P₄(y):=”y – высокопоставленное лицо”, P₅(y):=”y способствует провозу наркотиков”.

_y(P₃(y)P₄(y)_x(P₁(x)P₂(x,y)));

_y(P₃(y)P₅(y));

_y(P₃(y)P₄(yP₅(y));

---

_x(P₁(x)P₅(x)).

1) F₁= _y(P₃(y)P₅(y)) - посылка;

2) F₂=P₃(a)P₅(a) - заключение по формуле F₁ и правилу удаления квантора существования;

3) F₃= P₃(a) - заключение по формуле F₂ и правилу удаления логической связки конъюнкции;

4) F₄= P₅(a) - заключение по формуле F₂ и правилу удаления логической связки конъюнкции;

5) F₅=_y(P₃(y)P₄(yP₅(y)) посылка;

6) F₆= P₃(t)P₄(tP₅(t) - заключение по формуле F₅ и правилу удаления квантора общности;

7) F₇=P₃(t)P₄(t)P₅(t) - заключение по формуле F₆ и ее эквивалентным преобразованиям;

8) F₈=P₄(a) - заключение по формуле F₇ при t=a для P₃(a)=л и P₅(a)=л;

9) F₉=_y(P₃(y)P₄(y)_x(P₁(x)P₂(x,y))) - посылка;

10) F₁₀=_y_x (P₃(y)P₄(y) (P₁(x)P₂(x,y))) - заключение по формуле F₉ и правилу приведения к ПНФ;

11) F₁₁=P₃(a)P₄(a)P₁(t)P₂(t,a) - заключение по формуле F₁₀ и правилу удаления квантора общности;

12) F₁₂= P₃(a)P₄(a) - заключение по формулам F₃ и F₈ и правилу введения логической связки конъюнкции исчисления высказываний;

13) F₁₃=(P₁(t)P₂(t,a)) - заключение по формулам F₁₁ и F₁₂ и правилу modus ponens;

14) F₁₄= P₁(t) -заключение по формуле F13 и правилу удаления логической связки конъюнкции исчисления высказываний;

15) F₁₅=P₅(a)=P₅(t) -заключение по формуле F₄ и замене предметной постоянной термом;

16) F₁₆= P₁(t)P₅(t) -заключение по формулам F14 и А15 и правилу введения логической связки конъюнкция исчисления высказываний;

17) F₁₇=_x(P₁(x)P₅(x)) -заключение по формуле F16 и правилу введения квантора существования. Так доказана истинность формулы _x(P₁(x)P₅(x)).


_y(P₃(y)P₄(y)_x(P₁(x)P₂(x,y)))

_y(P₃(y)P₄(yP₅(y));


_y(P₃(y)P₅(y))

---

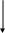
_y_x (P₃(y)P₄(y) (P₁(x)P₂(x,y)))

P₃(t)P₄(tP₅(t)



P₃(a)P₅(a)

P₃(a)P₄(a) P₁(t)P₂(t,a)





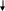
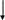
P₃(t)P₄(t)P₅(t)

P₃(a)

P₅(a)

(P₁(t)P₂(t,a))






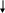
t
P₄(a)

P₁(t)
=a


P₃(a)P₄(a)


a=t
P₁(t)P₅(t)

P₅(t)





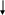
_x(P₁(x)P₅(x))


Рис. 11. Граф вывода заключения

Пример: Доказать истинность заключения

x( P₁(x)( P₂(x))); x(P₃(x)P₁(x))

x(P₃(x)( P₂(x))).

1) F₁=x( P₁(x)( P₂(x))) - посылка;

2) F₂=x(P₃ (x)P₁ (x)) -посылка;

3) F₃=(P₁ (t)( P₂ (t))) - заключение по формуле F₁ и правилу 2) удаления квантора общности;

4) F₄= P₃ (t) P₁ (t) - заключение по формуле F₂ и правилу 2) удаления квантора общности;

5) F₅= (P₃ (t)( P₂ (t))) - заключение по формулам F₃, F₄ и закону силогизма исчисления высказываний (см 1.2.3.2 правило 11);

6) F₆=_x(P₃(x)(P₂(x))) - заключение по формуле F

---