Файл: Описание контрольных измерительных материалов для проведения в 20212022 учебном году промежуточной аттестации по математике учащихся 10 класса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 27
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Описание контрольных измерительных материалов для проведения в 2021-2022 учебном году промежуточной аттестации по математике учащихся 10 класса
Основной целью проведения промежуточной аттестации является установление фактического уровня теоретических знаний, практических умений и навыков по предмету математика, соотнесение этого уровня с требованиями ФГОС СОО.
Структура КИМ.
Каждый вариант контрольной работы включает 9 заданий следующего содержания:
-
Уравнение -
Вычисления и преобразования -
Теория вероятности -
Текстовая задача -
Наибольшее и наименьшее значение функции -
Планиметрия -
Стереометрия -
Уравнение -
Стереометрия
Первые 7 заданий базового уровня, задания 8 и 9 – повышенного уровня сложности.
Система оценивания отдельных заданий и контрольной работы в целом
Задания 1-7 оценивается в 1 балл. Задание 8 и 9 оцениваются с учетом правильности и полноты ответа. Максимальный балл за решение уравнения и стереометрической задачи – 2 балла.
На основе баллов, выставленных за выполнение всех заданий работы, подсчитывается тестовый балл, который переводится в отметку по пятибалльной шкале в соответствии с рекомендуемой шкалой оценивания. Максимальное количество баллов за выполненную без ошибок работу – 11 баллов.
Рекомендуемая шкала оценивания:
11-9 баллов - «5» ;
8-6 баллов- «4» ;
5-3 баллов - «3»;
2 балла и менее - «2».
Продолжительность выполнения работы.
На выполнение всей контрольной работы отводится 90 минут.
Ответы
| Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Баллы | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 |
| Ответ:_Вариант_1'>Ответ: Вариант 1 | 87 | 5 | 0,3 | 13 | -3 | 5 | 17 | а) | |
| Ответ: Вариант 2 | 35 | -3 | 0,36 | 18 | 2 | 9,6 | 5 | а) | |
Кодификатор
Заданий для проведения промежуточной аттестации учащихся 10 класса по математике.
Уровни сложности заданий: Б - базовый, П-повышенный.
| Обозначение задания в работе | Проверяемые элементы содержания | Код проверяемого требования | Код элементов содержания | Уровень сложности задания | Макс. балл за выпол нение задания |
| | Уравнение | 1.6-1.13 | 1.1, 1.2 | Б | 1 |
| | Вычисления и преобразования | 1.14-1.18 | 1.1 | Б | 1 |
| | Теория вероятности | 1.19-1.21 | 1.4 | Б | 1 |
| | Текстовая задача | 1.28-1.30, 1.35-1.41 | 1.2 | Б | 1 |
| | Наибольшее и наименьшее значение функции | 1.31-1.34 | 1.3 | Б | 1 |
| | Планиметрия | 2.8-2.12 | 2.2, 2.3 | Б | 1 |
| | Стереометрия | 2.1-2.7 | 2.1, 2.2, 2.3 | Б | 1 |
| | Уравнение | 1.19-1.27 | 1.1-1.3 | П | 2 |
| | Стереометрия | 3.1-3.4 | 2.4 | П | 2 |
Промежуточная аттестация по математике 10 класс
Вариант 1
-
Найдите корень уравнения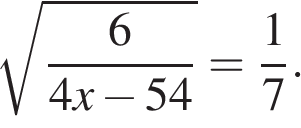
-
Найдите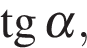 если
если 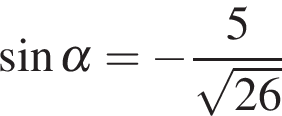 и
и 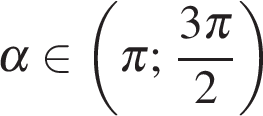
-
В классе 21 учащийся, среди них два друга — Вадим и Олег. Учащихся случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе. -
Кусок проволоки длиной 52 м сгибают так, чтобы образовался прямоугольник. Какую длину должны иметь стороны прямоугольника, чтобы его площадь была наибольшей? -
Найдите точку минимума функции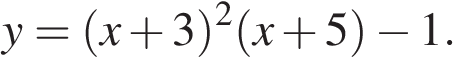
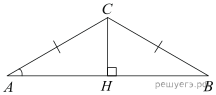
-
В треугольнике ABC AC = BC, AB = 9,6,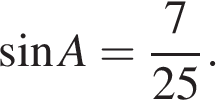 Найдите AC.
Найдите AC.
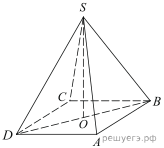
-
В правильной четырехугольной пирамиде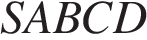 точка
точка  – центр основания,
– центр основания, 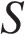 – вершина,
– вершина, 
 Найдите боковое ребро
Найдите боковое ребро 
-
а) Решите уравнение
б) Найдите корни этого уравнения, принадлежащие промежутку
-
В правильной четырёхугольной пирамиде SABCD сторона AB основания равна а высота SH пирамиды равна 3. Точки M и N — середины рёбер CD и AB, соответственно, а NT — высота пирамиды NSCD с вершиной N и основанием SCD.
а высота SH пирамиды равна 3. Точки M и N — середины рёбер CD и AB, соответственно, а NT — высота пирамиды NSCD с вершиной N и основанием SCD.
а) Докажите, что точка T является серединой SM.
б) Найдите расстояние между NT и SC.
Промежуточная аттестация по математике 10 класс
Вариант 2
-
Найдите корень уравнения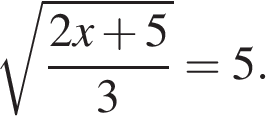
-
Найдите если
если 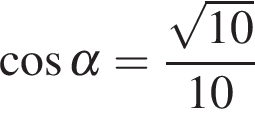 и
и 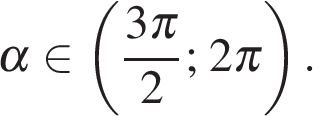
-
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 спортсменов из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России. -
Число 6 представьте в виде суммы двух неотрицательных чисел так, чтобы произведение этих чисел было наибольшим. -
Найдите точку максимума функции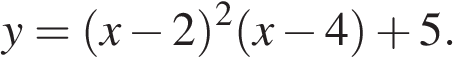
-
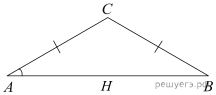
В треугольнике ABC AC = BC = 5, Найдите АВ.
Найдите АВ.

-
В правильной четырехугольной пирамиде точка
точка  – центр основания,
– центр основания,  – вершина,
– вершина, 
 Найдите длину отрезка
Найдите длину отрезка 
-
а) Решите уравнение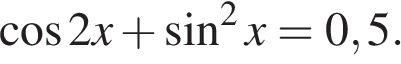
б) Найдите все корни этого уравнения, принадлежащие отрезку
-
В правильной четырёхугольной пирамиде SABCD боковое ребро SA равно а высота SH пирамиды равна
а высота SH пирамиды равна  Точки M и N — середины рёбер CD и AB, соответственно, а NT — высота пирамиды с вершиной N и основанием SCD.
Точки M и N — середины рёбер CD и AB, соответственно, а NT — высота пирамиды с вершиной N и основанием SCD.
а) Докажите, что точка T является серединой SM.
б) Найдите расстояние между NT и SC.