Файл: Линейные однородные дифферециальные уравнения второго порядка с постоянными коэффициентами.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
9ПОУРОЧНЫЙ ПЛАН
| Раздел: | ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ | |
| ФИО педагога | Амантаев В.А | |
| Дата: | 12.04.2023 | |
| Класс: | Количество присутствующих: | Количество отсутствующих: |
| Тема урока: | Линейные однородные дифферециальные уравнения второго порядка с постоянными коэффициентами. | |
| Цели обучения в соответствии с учебной программой: | 11.4.1.25. Решать линейные однородные дифференциальные уравнения 2 порядка вида ay′′ + by′ + cy = 0, где a, b, c – постоянные | |
| Цели урока: | Отработать знания и умения а также решение задач на линейные однородные дифферециальные уравнения второго порядка с постоянными коэффициентами. | |
Ходурока
| Этапурока/ Время | Действия педагога | Действияученика | Оценивание | Ресурсы |
| Приветствие, создание коллаборативной среды/ 2 мин | Приветствие со школьниками, определение отсутствующих. Сообщение темы и цели урока, ожидаемых результатов. | Принимают участие в постановке темы (цели) урока. Осмысливают поставленную цель. | | |
| Актуализация знаний/ 5 мин. Проверка домашнего задания | Повторения пройденного материала по стратегии «Я знаю, что…..» Корни уравнений | Говорят, что знают по теме урока Взаимопроверка | ФО Похвала учителя | |
| Середина урока 35 минут | Данные уравнения имеют вид: где p и q –постоянные числа Определение Два решения уравнения (1) Теорема ( Об общем решении ЛОДУ) Если где Характеристическое уравнение Для нахождения общего решения (2) следует найти два линейно независимых частных решения. Будем искать их виде -характеристическое уравнение, его корни: Случаи решения характеристического уравнения: I. корни II. корни III корни Рассмотрим каждый случай отдельно. I. Корни характеристического уравнения действительные и различные ( Частными решениями будут функции Они линейно независимы, т.к. Следовательно, общее решение имеет вид: II. Корни характеристического уравнения действительные и равные ( Это будет при D=0 , т.е. В качестве первого частного решения возьмём Подставим в (1): Итак, в случае IІI. Корни характеристического уравнения комплексные Частные решения: Покажем, что если некоторая комплексная функция Значит, в качестве частных решений уравнения (1) можно взять отдельно действительные и мнимые части решений (5): В этом случае общее решение уравнения (1) можно представить в виде где Важным частным случаем решения (6) является случай, когда в уравнении (1) p=0 и q При этом характеристическое уравнение Примеры: Найти общее решение линейных однородных дифференциальных уравнений с постоянными коэффициентами. 1) Характеристическое уравнение: 2) Общее решение: 3) Общее решение: 4) Общее решение: 5) Общее решение: 6) Общее решение: 7) Общее решение: 8) Общее решение: Самостоятельное работа Найти общее решение следующих дифференциальных уравнений. Задание 1. 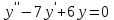 Решение: Составим характеристическое уравнение: 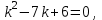  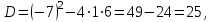 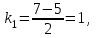 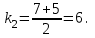 Общее решение данного дифференциального уравнения, согласно формуле(1), имеет вид: 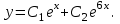 Ответ: 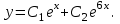 Задание 2. 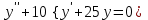 Решение: Составим характеристическое уравнение: 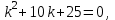 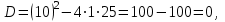  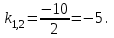 Общее решение данного дифференциального уравнения, согласно формуле(2), имеет вид: 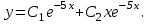 Ответ: 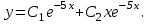 Задание 3. 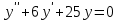 . .Решение: Составим характеристическое уравнение: 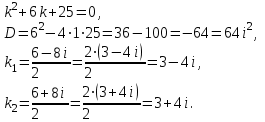 Общее решение данного дифференциального уравнения, согласно формуле(3), имеет вид: 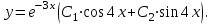 Ответ: 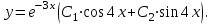 Задание 4 . 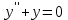 Составим характеристическое уравнение: 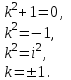 Это третий случай, где 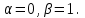 Общее решение данного дифференциального уравнения, согласно формуле(3), имеет вид: 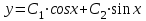 Ответ: 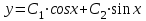 Задание 5.Найти частное решение дифференциального уравнения 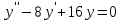 , если у(0)=1 и , если у(0)=1 и 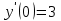 . .Решение: Составим характеристическое уравнение: 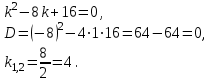 Общее решение данного дифференциального уравнения, согласно формуле(2), имеет вид: 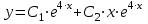 Так как заданы начальные условия, то: 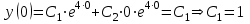 Чтобы найти значение 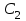 , дифференцируем общее решение. , дифференцируем общее решение.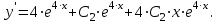 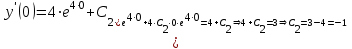 Таким образом, искомое частное решение имеет вид 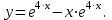 Ответ: 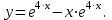 Решите дифференциальное уравнение: y′′+4y′+5y=0. №2.Решите уравнение: y′′+25y=0. №3. Найдите общее решение уравнения и выполните проверку: 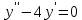 №4. Решите дифференциальное уравнение: №5. Решите дифференциальное уравнение: №6.Найдите общее решение уравнений 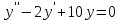 . .№7. Решите однородное дифференциальное уравнения второго порядка: №8. Найти часное решение дифференциального уравнения, удовлетворяющее начальное условиям: 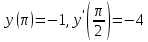 , ,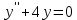 . .Задания: 28.1, 28.2, 28.3, 28.4, 28.5, 28.6, 28.7 | Внимательно слушает и высказывает свое мнение Внимательно слушает и анализирует объясняемый материал | Устный комментарий учителя Похвала учителя Взаимооценивание | Презентация |
| Конец урока Рефлексия/3 мин. Запись домашнего задания |
| производят рефлексию по пройденной теме по стратегии «незаконченные фразы» записывают домашнее задание | Комментирует домашнее задание | |