ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2024
Просмотров: 27
Скачиваний: 0
Силовой расчет плоских рычажных механизмов.
Задан кривошипно – ползунный механизм
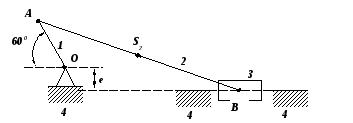
Исходные данные:
Линейные размеры:
мм,
мм;
мм;
мм;
Скорость
вращения ведущего звена
–
рад/с.
Расчетные
положения ведущего звена
–
;
.
Массы звеньев
–
кг;
кг;
кг.
Момент
инерции звена 2
относительно
центра
–
кг·м2.
Усилие
сопротивления движению ползуна
–
Н
Результаты кинематического расчета:
Положение 600
Линейные ускорения :
м/с2
;
м/с2
;
м/с2
Угловое
ускорение
–
рад/с2
(против часовой стрелки.
Положение 1500
Линейные ускорения :
м/с2
;
м/с2
;
м/с2
Угловое
ускорение
–
рад/с2
(против часовой стрелки.
Порядок выполнения расчетов и графических построений по каждому принятому положению механизма.
1 Положение механизма – угол поворота кривошипа 600
1.1 Вычерчиваем
план механизма в масштабе
мм/мм
1.2 Выполняем структурный анализ
Механизм 2 класса; 2 порядка.
Формула строения
механизма –
.
1.3 Выполняем кинематический расчет механизма с определением линейных ускорений точек и угловых ускорений звеньев:
м/с2
;
м/с2
;
м/с2
рад/с2
(против
часовой стрелки).
1.4 Определяем силы инерции, моменты сил инерции и веса звеньев.
Силы инерции
–
Н
Н
Н
Момент сил инерции
Нм (по часовой
стрелке).
Веса звеньев
:
Н
Н
Н
1.5 Дополняем кинематическую схему до динамической.
При этом условно заменяем моменты от сил инерции и удерживающий момент пара сил, приложенных на концах соответствующих звеньев.
Н
1.6 Выполняем силовой расчет механизма
1.6.1 Расчет начинается с группы, наиболее удаленной от ведущего звена (звена с уравновешивающим моментом) – группа 2 – 3..
Вычерчиваем группу в масштабе перемещений. Переносим на группу все силы, учитывая и инерционные силы. Отброшенные звенья заменяем реакциями от них.
Такими силами являются :
реакция от
звена 4 –
;
реакция от
звена 2 –
.
В соответствии с методом кинетостатики векторная сумма всех сил, приложенных к рассматриваемому элементу механизма, включая и силы инерции равна нулю.
Поэтому для группы 2 – 3 имеем
В векторном уравнении имеются три неизвестных. Для возможности графического решения необходимо предварительно определить одно из таких неизвестных.
Для этого используем уравнение равенство нулю моментов всех сил относительно точки В.
Плечи
и
находим из чертежа.
;
В соответствии
с уравнением равновесия кинетостатики
строим векторный многоугольник из
которого находим вектора
и
.
Для построения принимаем масштаб сил kP = 20 Н/мм.
Длины отрезков, соответствующие величине векторов сил в масштабе, равны:
;
;
;
;
;
.
Из векторного многоугольника находим длину отрезков:
;
.
С учетом масштаба величина искомых усилий составляет:
Рассмотрим отдельно равновесия звена 2 с учетом сил инерции и давления в шарнире В от звена 3.
Величина давления со стороны звена 1 равна
Уравнение равновесия в векторной форме будет следующим
.
Построив векторный многоугольник, можно найти величину давления в шарнире В.
Длина отрезка , соответствующая величине вектора давления в шарнире В, равна
Величина усилия с учетом масштаба равна
1.6.2 Выполняем расчет начального звена.
Вычертим начальное звено в масштабе и приложим к нему все силы с учетом инерционных и давления в точке А со стороны звена 2.
.
Составляем уравнение моментов относительно точки О по методу кинетостатики.
Величины плеч сил в расчетном уравнении берем с чертежа группы [ 4 – 1 ].
;
Следовательно:
Удерживающий момент составит
Определим усилие в шарнире О из условия динамического равновесия звена 1.
Строим векторный многоугольник.
Размеры отрезков, соответствующие в масштабе величине векторов, будут равны:
;
;
Отрезок, соответствующий величине вектора Р41 , равен
Величина вектора Р41 с учетом масштаба равна
1.7 Определяем величину удерживающего момента с помощью рычага Жуковского.
Вычерчиваем кинематическую схему механизма с учетом всех сил, включая силы инерции.
Вычерчиваем план скоростей, повернутый на 90 0, и в соответствующие точки переносим все силы
Записываем уравнение динамического равновесия моментов всех сил относительно полюса « р ».
Величины плеч берем с чертежа
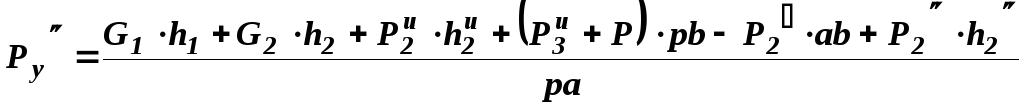
Удерживающий момент равен