ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.07.2024
Просмотров: 15
Скачиваний: 0
§ 11. Параметрические уравнения линии
Обозначим буквами х и у координаты некоторой точки М; рассмотрим две функции аргумента t:
![]()
П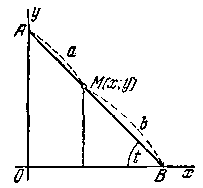 ри
изменении t величины
х и
у будут,
вообще говоря, меняться, следовательно,
точка М будет
перемещаться. Равенства (1) называются
параметрическими уравнениями линии,
которая является траекторией точки М;
аргумент t
носит название
параметра. Если из равенства (1) можно
исключить параметр t,
то получим уравнение
траектории точки М в
виде
ри
изменении t величины
х и
у будут,
вообще говоря, меняться, следовательно,
точка М будет
перемещаться. Равенства (1) называются
параметрическими уравнениями линии,
которая является траекторией точки М;
аргумент t
носит название
параметра. Если из равенства (1) можно
исключить параметр t,
то получим уравнение
траектории точки М в
виде
F(x, y) = 0.
204. Стержень АВ скользит своими концами А к В по координатным осям. Точка М делит стержень на две части АМ = а и ВМ = b. Вывести параметрические уравнения траектории точки М, приняв в качестве параметра
Черт. 8. угол t = <OBA (черт. 8). Исключить затем параметр t и найти уравнение траектории точки М в виде F(x, y) = 0
205. Траекторией точки М является эллипс, уравнение которого
![]() (см. задачу 190). Вывести параметрические
уравнения траектории точки М,
принимая в качестве
параметра t угол
наклона отрезка ОМ к
оси Ох.
(см. задачу 190). Вывести параметрические
уравнения траектории точки М,
принимая в качестве
параметра t угол
наклона отрезка ОМ к
оси Ох.
2 06.
Траекторией точки М
является гипербола,
уравнение которой
06.
Траекторией точки М
является гипербола,
уравнение которой
![]() (см.
задачу 191). Вывести параметрические
уравнения траектории точки М,
принимая в качестве
параметра t угол
наклона отрезка ОМ к
оси Ох.
(см.
задачу 191). Вывести параметрические
уравнения траектории точки М,
принимая в качестве
параметра t угол
наклона отрезка ОМ к
оси Ох.
207. Траекторией точки М является парабола, уравнение которой у2 =2рх (см. задачу 192). Вывести параметрические уравнения траектории точки М, принимая в качестве параметра t:
1) ординату точки М;
2) угол наклона отрезка ОМ к оси Ох;
3) угол наклона отрезка FM к оси Ох, где точка F — фокус параболы.
208. Даны полярные уравнения следующих линий:
1)
= 2Rcos;
2)
= 2Rsin;
3)
= 2p![]() .
.
Составить параметрические уравнения этих линий в декартовых прямоугольных координатах, совмещая положительную полуось абсцисс с полярной осью и выбирая в качестве параметра полярный угол.
209. Даны параметрические уравнения линий:
1)![]() 2)
2)
![]() 3)
3)
![]()
8
4)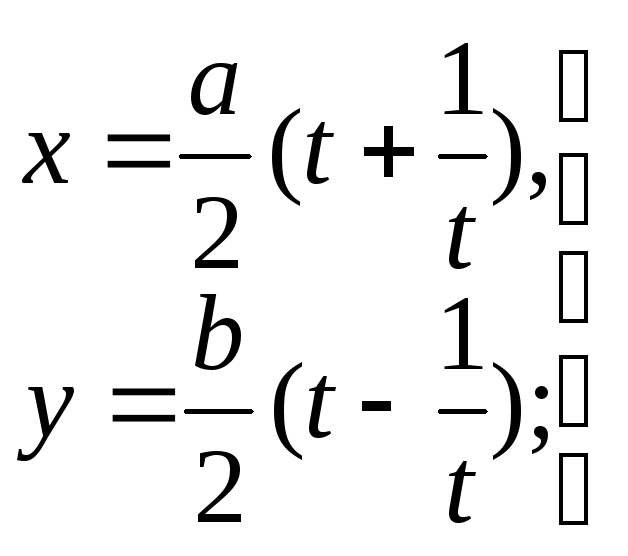 5)
5)
![]() 6)
6)
![]()
7)
![]()
исключив параметр t, найти уравнения этих линий в виде
F(x, y) = 0