§ 13. Неполные уравнения прямой. Совместное исследование

уравнений двух и трёх прямых. Уравнение прямой «в отрезках»

Если в общем уравнении прямой

Ах + Ву + С = 0 (1)

один или два из трёх коэффициентов (считая и свободный член) обращаются в нуль, то уравнение называется неполным. Возможны следующие случаи:

1) С = 0; уравнение имеет вид Ах +By = 0 и определяет прямую, про­ходящую через начало координат.

2) B = 0 (A≠0); уравнение имеет вид Ах + С = 0 и определяет прямую,

перпендикулярную к оси Ох. Это уравнение может быть записано в виде х = а, где является величиной отрезка, который отсекает прямая на оси Ох, считая от начала координат.

3) B = 0, С = 0 (A≠0); уравнение может быть записано в виде х = 0 и определяет ось ординат.

4) А=0 (B≠0); уравнение имеет вид By + С = 0 и определяет прямую, перпендикулярную к оси Оу. Это уравнение может быть записано в виде y = b , где является величиной отрезка, который отсекает прямая на оси Оу, считая от начала координат.

5) А = 0, С = 0 (B≠0); уравнение может быть записано в виде у = 0 и определяет ось абсцисс.

Если ни один из коэффициентов уравнения (1) не равен нулю, то его можно преобразовать к виду

где и суть величины отрезков, которые отсекает прямая

на координатных осях.

Уравнение (2) называется уравнением прямой «в отрезках».

Если две прямые даны уравнениями

A₁ + B₁ y + C₁ = 0,

то могут представиться три случая:

а) — прямые имеют одну общую точку;

б) — прямые параллельны;

в) — прямые сливаются, т. е. оба уравнения

---

определяют одну и ту же прямую.

285. Определить, при каком значении а прямая

(а + 2)x + (а² – 9)y + 3а² – 8а + 5 = О

1) параллельна оси абсцисс;

2) параллельна оси ординат;

3) проходит через начало координат.

В каждом случае написать уравнение прямой.

286. Определить, при каких значениях т и п прямая

(т + 2п – 3) х + (2т – n + 1)y +6m + 9 = 0

параллельна оси абсцисс и отсекает на оси ординат отрезок, рав­ный – 3 (считая от начала координат). Написать уравнение этой прямой.

287. Определить, при каких значениях тип прямая

(2т – п + 5) х + (т + 3n – 2) у + 2m + 7n + 19 = 0

параллельна оси ординат и отсекает на оси абсцисс отрезок, рав­ный +5 (считая от начала коорди2ат). Написать уравнение этой прямой.

288. Доказать, что в следующих случаях две данные прямые пересекаются, и найти точку их пересечения:

1) х + 5у – 35 = 0, Зх+2у – 27 = 0;

2) 14х – 9у – 24 = 0, 7x –2у – 17 = 0;

3) 12x + 15y – 8 = 0, 16x + 9у – 7 = 0;

4) 8х – 33у – 19 = 0, 12х + 55у – 19 = 0;

5) 3x + 5 = 0, у – 2 = 0.

289. Доказать, что в следующих случаях две данные прямые параллельны:

1) 3х + 5у – 4 = 0, 6x + 10y + 7 = 0;

2) 2x – 4у + 3 = 0, x – 2y = 0;

3) 2x – 1 = 0, x + 3 = 0;

4) у + 3=0, 5y – 7 = 0.

290. Доказать, что в следующих случаях две данные прямые совпадают:

1) 3x + 5y – 4 = 0, 6x + 10y – 8 = 0;

2) x – y = 0, х– 2у = 0;

3) x– 1 = 0, 3х – = 0.

291. Определить, при каких значениях а и b две прямые

аx – 2y – 1 = 0, 6x – 4y – b = О

1) имеют одну общую точку; 2) параллельны; 3) совпадают.

292. Определить, при каких значениях т и п две прямые

---

тх + 8у + n = 0, 2х + ту – 1 = 0

1) параллельны; 2) совпадают; 3) перпендикулярны.

293. Определить, при каком значении т две прямые

(m — 1)x + my — 5 = 0, mx + (2m — 1)y + 7= 0

пересекаются в точке, лежащей на оси абсцисс.

294. Определить, при каком значении т две прямые

mx + (2m + 3 + m + 6 = 0, (2m + 1)x + (m — 1)y + m — 2= 0

пересекаются в точке, лежащей на оси ординат.

295. Установить, пересекаются ли в одной точке три прямые в следующих случаях:

1) 2х + 3у— 1 = 0, 4x— 5у + 5 = 0, 3x—у + 2 = 0;

2) 3x—y + 3 = 0, 5x +3y — 7 = 0, х — 2у — 4 = 0;

3)2х — у+1= 0, х + 2у—17= 0, х + 2у — 3 = 0,

296—306) § 13. неполные уравнения прямой 49 296. Доказать, что если три прямые

A₁ +B ₁ y +С₁ = 0, A₁ +B₂ y +C = 0 A₃ x +B ₃ y +С₃ = 0

пересекаются в одной точке, то

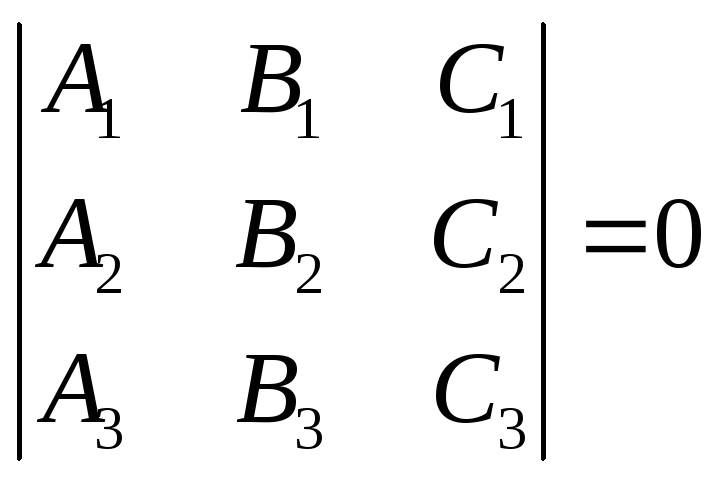
297. Доказать, что если 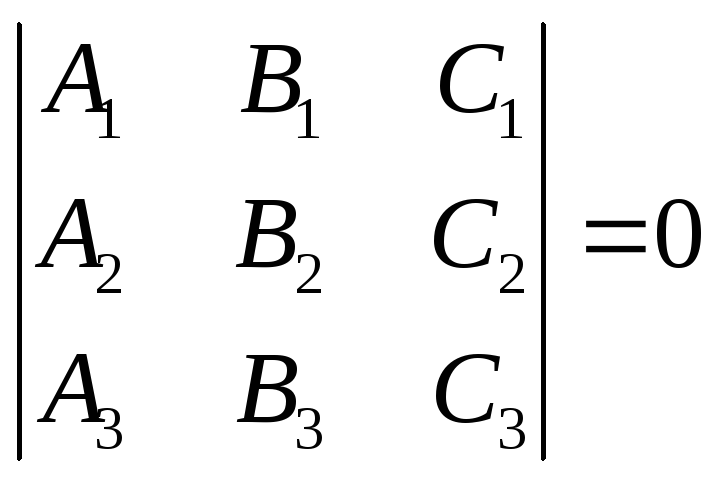то три прямые

A₁x + B₁y + С₁ = 0, A₂ x + B₂y + C = 0 A₃x + B₃y + С₃ = 0

пересекаются в одной точке или параллельны.

298. Определить, при каком значении а три прямые 2х — у + 3 = 0,

х + y + 3 = 0, ах + y — 13 = 0 будут пересекаться в одной точке.

299. Даны прямые: 1) 2x + 3у — 6 = 0; 2) 4x—3y + 24 = 0; 3) 2х + 3y — 9= 0;

4) 3x — 5у — 2 = 0; 5) 5x + 2у— 1 = 0.

Составить для них уравнения «в отрезках» и построить эти прямые на чертеже.

300. Вычислить площадь треугольника, отсекаемого прямой 3 х — 4у — 12 = 0 от координатного угла.

301. Составить уравнение прямой, которая проходит через точку M₁(3; —7) и отсекает на 2оординатных осях отличные от нуля отрезки одинаковой величины (считая каждый отрезок направленным от начала координат).

302. Составить уравнение прямой, которая проходит через точку Р(2; 3) и отсекает на координатных осях отрезки равной длины, считая каждый отрезок от начала координат.

---

303. Составить уравнение прямой, которая проходит через точку С(1; 1) и отсекает от координатного угла треугольник с площадью, равной 2 кв. ед.

304. Составить уравнение прямой, которая проходит через точку В(5; —5) и отсекает от координатного угла треугольник с пло­щадью, равной 50 кв. ед.

305. Составить уравнение прямой, которая проходит через точку P(8; 6) и отсекает от координатного угла треугольник с площадью, равной 12 кв. ед.

306. Составить уравнение прямой, которая проходит через точку Р(12; 6) и отсекает от координатного угла треугольник с пло­щадью, равной 150 кв. ед.

307. Через точку М(4;3) проведена прямая, отсекающая от координатного угла треугольник, площадь которого равна 3 кв. ед. Определить точки пересечения этой прямой с осями координат.

308. Через точку М₁ (х₁; у ₁), где x₁у₁>0, проведена прямая

отсекающая от координатного угла треугольник, площадь которого равна S. Определить, при каком соотношении между величинами x ₁> y₁ и S отрезки а и b будут иметь одинаковые знаки.

---

Смотрите также файлы

• kletenik_12.doc

• kletenik_11.doc

• kletenik_10.doc

• kletenik_09.doc

• kletenik_08.doc