§ 42. Направляющий вектор прямой. Канонические уравнения прямой. Параметрические уравнения прямой

Каждый не равный нулю вектор, лежащий на данной прямой или парал­лельный ей, называется направляющим вектором этой прямой.

Направляющий вектор произвольной прямой в дальнейшем обозначается буквой а, его координаты — буквами l, т, т

а = {l; т; п}.

Если известна одна точка М₀ (х₀; у₀; z₀) прямой и направляющий вектор а = {l; т; п}. то прямая может быть определена (двумя) уравне­ниями вида:

(1)

В таком виде уравнения прямой называются каноническими.

Канонические уравнения прямой, проходящей через две данные точки

М₁ (х₁; у₁; z₁ ) и М₂ (х₂; у₂; z₂) имеют вид:

(2)

Обозначим буквой t каждое из равных отношений в канонических урав­нениях (1); мы получим:

Отсюда 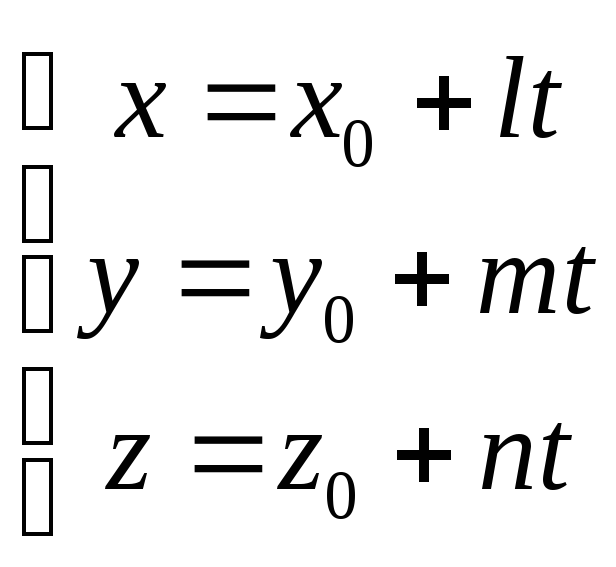(3)

Это — параметрические уравнения прямой, проходящей через точку М₁ (х₁; у₁; z₁ ) в направлении вектора а = {l; т; п}. В уравнениях (3) t рас­сматривается как произвольно изменяющийся параметр х, у, z — как функции от t; при изменении t величины х, у, z меняются так, что точка М (х; у; z) движется по данной прямой.

Если параметр t рассматривать как переменное время, а уравнения (3), как уравнения движения точки М, то эти уравнения будут определять пря­молинейное и равномерное движение точки М. При t = 0 точка М совпадает с точкой M₀. Скорость υ точки М постоянна и определяется формулой

υ =

1007. Составить канонические уравнения прямой, проходящей через точку

М ₁ (2; 0; —3) параллельно:

---

1) вектору а = {2; —3; 5};

2) прямой

3) оси Ох; 4) оси Оу; 5) оси Oz.

1008. Составить канонические уравнения прямой, проходящей через две данные точки:

1) (1; — 2; 1), (3; 1; —1); 2) (3; —1; 0),(1; 0, —3);

3) (0; —2; 3), (3; -2; 1); 4) (1; 2; —4), (—1; 2; —4).

1009. Составить параметрические уравнения прямой, проходящей через точку

М₁;( —1; —3) параллельно

1) вектору а = {2; —3; 4};

2) прямой

3) прямой х=3е— 1, у = — 2е+3, z = 5t + 2.

1010.Составить параметрические уравнения прямой, проходящей через две данные точки: 1) (3; —1, 2), (2; 1; 1); 2) (1; 1; —2), (3; —1; 0); 3) (0; 0; 1), (0; 1; —2).

1011. Через точки M ₁ (—6; 6; —5) и М₂(12; —6; 1) прове­дена прямая. Определить точки пересечения этой прямой с коорди­натными плоскостями.

1012. Даны вершины треугольника А(3; 6; —7), В(—5; 2; 3) и С(4; —7; —2). Составить параметрические уравнения его меди­аны, проведённой из вершины С.

1013. Даны вершины треугольника А(3; —1; —1), В(1; 2; — 7) и С(—5; 14; —3). Составить канонические уравнения биссектрисы его внутреннего угла при вершине В.

1014. Даны вершины треугольника А (2; — 1; — 3), В (5; 2; — 7) и С(—7; 11; 6). Составить канонические уравнения биссектрисы его внешнего угла при вершине А.

1015. Даны вершины треугольника А(1;—2;—4), В(3; 1; — 3) и С(5; 1; —7). Составить параметрические уравнения его высоты, опущенной из вершины В на противоположную сторону.

1016. Дана прямая

Вычислить проекции на оси координат какого-нибудь её направляю­щего вектора а. Найти общее выражение проекций на оси коорди­нат произвольного направляющего вектора этой прямой,

1017. Дана прямая

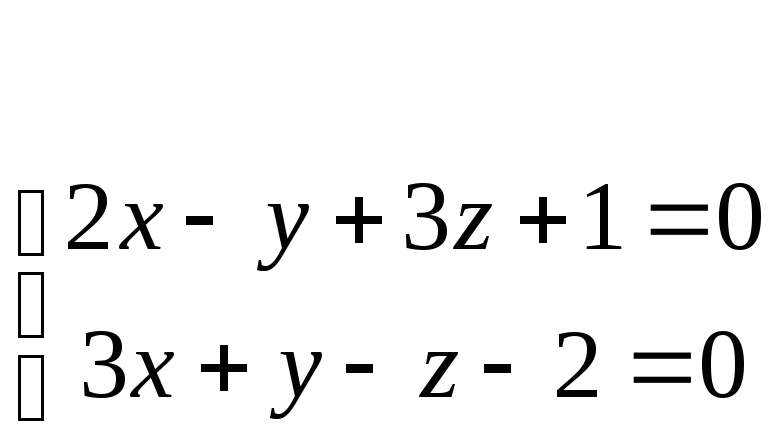
Найти разложение по базису i, j, k какого-нибудь её направляю­щего вектора а. Выразить в общем виде разложение по базису i, j, k произвольного направляющего вектора этой прямой.

1018. Составить канонические уравнения прямой, проходящей через точку М₁(1; 3; —5) параллельно прямой

---

1019. Составить канонические уравнения следующих прямых:

1) 2)

3)

1020. Составить параметрические уравнения следующих прямых:

1) 2)

1021. Доказать параллельность прямых:

1) и

2) , , и

3) и

1022. Доказать перпендикулярность прямых:

1) и

2) , , и

3) и

1023. Найти острый угол между прямыми:

,

1024. Найти тупой угол между прямыми:

х = 3t — 2 у = 0, z =-t + 3;

х = 2t —1, у = 0, z = t — 3.

---

1025. Определить косинус угла между прямыми:

1026. Доказать, что прямые, заданные параметрическими уравне­ниями х=2t — 3,

у = 3t — 2,z= —4t+6 и x=t + 5, у =— 4t—1, z =t— 4, пересекаются.

1027. Даны прямые

,

при каком значении / они пересекаются?

1028. Доказать, что условие, при котором две прямые

, и

лежат в одной плоскости, может быть представлено в следующем виде:

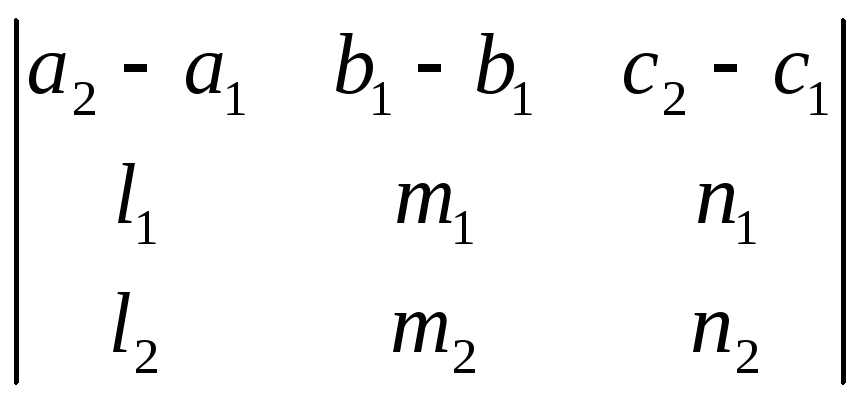=0

1029. Составить уравнения прямой, которая проходит через точку М₁(— 1; 2; — 3) перпендикулярно к вектору α = {6; — 2; — 3} и пересекает прямую

.

1030. Составить уравнения прямой, которая проходит через точку М₁(— 4; -5; 3) и пересекает две прямые

.

1031. Составить параметрические уравнения общего перпенди­куляра двух прямых, заданных уравнениями

х=3t —7, у = —2t+4, z = 3t + 4

х = t+1, y = 1t — 9, z= —t- 12.

1032. Даны уравнения движения точки М₁ (х; у; г)

х = 3 —4t, y = 5 + 3t, z = —2 + 12t.

Определить её скорость υ.

1033. Даны уравнения движения точки М₁ (х; у; г)

x = 5 — 2t, y = —3 + 2t, z = 5 — t.

Определить расстояние d, которое пройдёт эта точка за промежу­ток времени от t₁= 0 до t₂ = 7

---

1034. Составить уравнения движения точки М (х; у; z), которая, имея начальное положение М₀(3; —1;—5), движется прямолинейно и равномерно в направлении вектора s = {—2; 6; 3} со скоростью υ = 21.

1035. Составить уравнения движения точки М (х; у; z), которая, двигаясь прямолинейно и равномерно, прошла расстояние от точки М₁ (—7; 12; 5) до точки М₂ (9; —4, —3) за промежуток времени t₁ = 0 до t₂ = 4.

1036. Точка М (х; у; z) движется прямолинейно и равномерно из начального положения М₀(20; — 18; — 32) в направлении, проти­воположном вектору s = {3; —4; —12}, со скоростью υ=26. Составить уравнения движения точки М и определить точку, с ко­торой она совпадёт в момент времени t = 3.

1037. Точки М (х; у; z) и N (х; у; г) движутся прямолинейно и равномерно: первая из начального положения M₀ (— 5; 4; — 5) со скоростью υ_M=14 в направлении вектора s = {3; —6; 2}, вторая из начального положения N₀ (—5; 16; —6) со скоростью υ_N = 13 в направлении, противоположном вектору r={—4; 12; —3}. Со­ставить уравнения движения каждой из точек и, убедившись, что их траектории пересекаются, найти:

1) точку Р пересечения их траекторий;

2) время, затраченное на движение точки М от М₀ до Р;

3) время, затраченное на движение точки N от N ₀ до Р;

4) длины отрезков М₀ Р и N₀Р.

---

Смотрите также файлы

• kletenik_41.doc

• kletenik_40.doc

• kletenik_39.doc

• kletenik_38.doc

• kletenik_36.doc