§ 43. Смешанные задачи, относящиеся к уравнению

плоскости и уравнениям прямой

1038. Доказать, что прямая

х=3t — 2, у = — 4t+1, z = 4t —5

параллельна плоскости 4х — 3у — 6z — 5 = 0.

1039. Доказать, что прямая

лежит в плоскости 4х — Зу + 7z — 7 = 0.

1040. Найти точку пересечения прямой и плоскости:

1) , ;

2) , ;

3) , ;

1041. Составить канонические уравнения прямой, проходящей через точку

М₀ (2; -4; -1) и середину отрезка прямой

заключённого между плоскостями

, ,

1042. Составить уравнения прямой, проходящей через точку М₀ (2; — 3; — 5) перпендикулярно к плоскости 6х — Зу — 5z + 2 = 0.

1043. Составить уравнение плоскости, проходящей через точку М₀(1; —1; —1) перпендикулярно к прямой

,

1044. Составить уравнение плоскости, проходящей через точку M₀ (1; —2; 1) перпендикулярно к прямой

1045. При каком значении т прямая

,

параллельна плоскости

х — Зу + 6z + 7 = 0?

1046. При каком значении С прямая

параллельна плоскости

---

2x—у + Сz —2 = 0?

1047. При каких значениях А и D прямая

х=3 + 4t, у=1— 4t, z = —3 +t

лежит в плоскости

Ах + 2у— 4z + D = 0?

1048. При каких значениях А и В плоскость

Ах + Ву + Зz — 5 = 0

перпендикулярна к прямой

х = 3 + 2t, у = 5 —3t, z = — 2 — 2t?

1049. При каких значениях t и С прямая

перпендикулярна к плоскости

Зх — 2у + Сz+1=0?

1050. Найти проекцию точки Р(2; — 1; 3) на прямую

х=3t, , у=5t— 7, z = 2t + 2.

1051. Найти точку Q, симметричную точке Р(4; 1; 6) отно­сительно прямой

1052. Найти точку Q, симметричную точке Р(2; —5; 7) отно­сительно прямой, проходящей через точки M₁ (5; 4; 6) и М₂ (— 2; —17; —8).

1053. Найти проекцию точки Р(5; 2; —1) на плоскость

2x-y+3z+23=0.

1054. Найти точку Q, симметричную точке Р(1; 3; —4) отно­сительно плоскости

Зх+у — 2z = 0.

1055. На плоскости Оху найти такую точку Р, сумма расстоя­ний которой до точек А(—1; 2; 5) и В (11; —16; 10) была бы наименьшей.

1056. На плоскости Oxz найти такую точку Р, разность рас­стояний которой до точек M₁ (3; 2; —5) и М₂(8; —4; — 13) была бы наибольшей.

1057. На плоскости

2х — Зу + Зz— 17 = 0

найти такую точку Р, сумма расстояний которой до точек А (3; — 4; 7) и В(—5; —14; 17) была бы наименьшей.

1058. На плоскости

2х + 3у —4z—15 = 0

найти такую точку Р, разность расстояний которой до точек M₁ (5; 2; —7) и M₂(7; —25; 10) была бы наибольшей.

1059. Точка М(х; у; г) движется прямолинейно и равномерно из начального положения М₀ (15; — 24; —16) со скоростью υ=12 в направлении вектора s = {—2; 2; 1}. Убедившись, что траектория точки М пересекает плоскость Зх + 4у +7z — 17 = 0, найти:

1) точку Р их пересечения;

2) время, затраченное на движение точки М от M₀ до Р;

3) длину отрезка М₀Р.

1060. Точка М (х; у; z) движется прямолинейно и равномерно из начального положения М₀ (28; —30; —27) со скоростью υ=12,5 по перпендикуляру, опущенному из точки М₀ на плоскость 15х—16у—122+26=0. Составить уравнения движения точки М и определить:

---

1) точку Р пересечения ей траектории с этой плоскостью;

2) время, затраченное на движение точки М от М₀ до Р;

3) длину отрезка М₀Р.

1061. Точка М(х; у; z) движется прямолинейно и равномерно из начального положения М₀(11—21; 20) в направлении вектора s = {—1; 2; —2} со скоростью υ=12. Определить, за какое время она пройдёт отрезок своей траектории, заключённый между параллельными плоскостями:

2х+3у + 5z —41=0, 2х + 3у+ 5z+31 =0.

1062. Вычислить расстояние d точки Р(1; —1; —2) от прямой

1063. Вычислить расстояние d от точки Р(2; 3; — 1) до следую­щих прямых:

1) ;

2) x-1+1; y=t+2, z=4t+13;

3)

1064. Убедившись, что прямые

параллельны, вычислить расстояние d между ними.

1065. Составить уравнение плоскости, проходящей через точку M₁(1; 2; —3) параллельно прямым

,

1066. Доказать, что уравнение плоскости, проходящей через точку М₀ (х₀; у₀; z₀) параллельно прямым

,

может быть представлено в следующем виде:

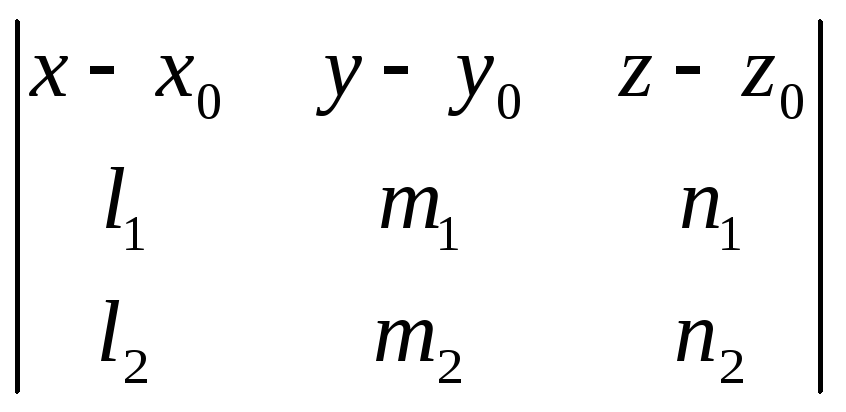=0

1067. Доказать, что уравнение плоскости, проходящей через точки М₁ (х₁; у₁; z₁ ) и М₂ (х₂; у₂; z₂) параллельно прямой

может быть представлено в следующем виде:

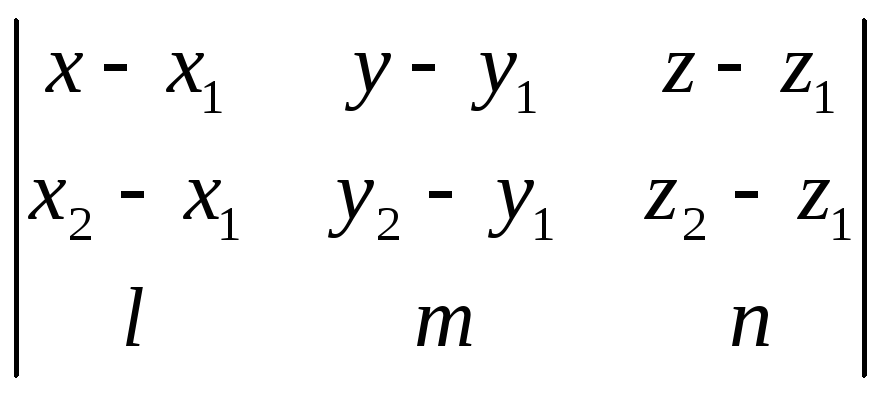=0

---

1068. Составить уравнение плоскости, проходящей через прямую

x= — x=2t+1; y=-3t+2; z=2t-3

и точку M₁ (2; —2; 1).

1069. Доказать, что уравнение плоскости, проходящей через прямую

х = х₀ + lt, у=у₀ +mt, z = z₀ +nt

и точку М₁ (х₁; у₁; z₁ ), может быть представлено в следующем виде:

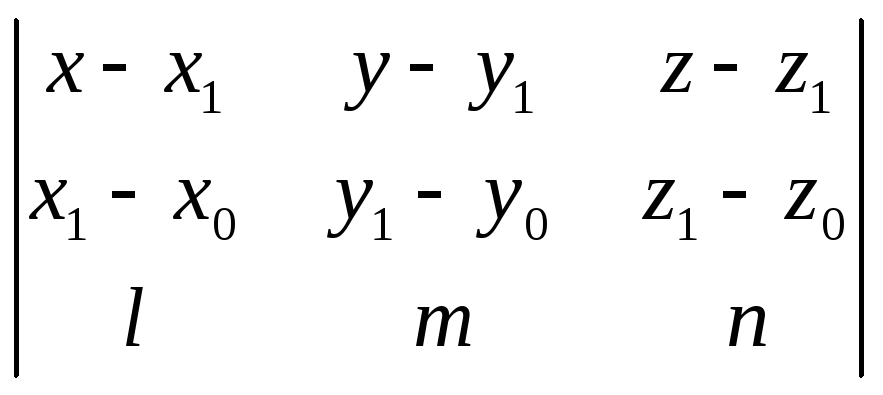=0

1070. Доказать, что прямые

и x=3е+7, y=2t+2; z=-2t+1

лежат в одной плоскости, и составить уравнение этой плоскости.

1071. Доказать, что если две прямые

,

пересекаются, то уравнение плоскости, в коюрой они лежат, может быть представлено в следующем виде:

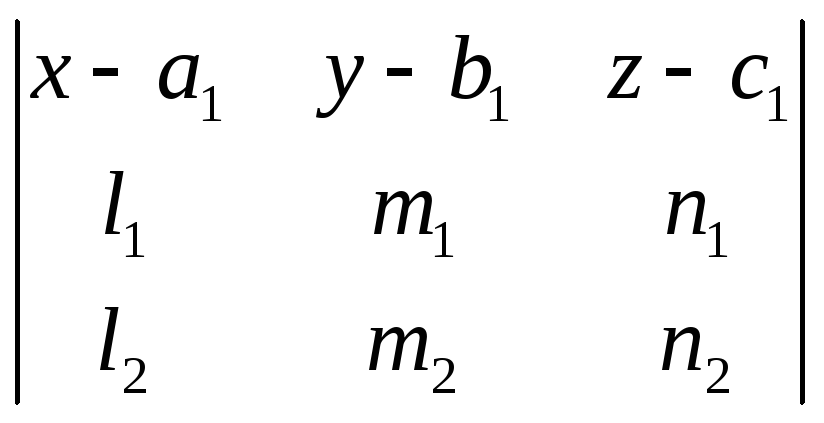=0

1072. Составить уравнение плоскости, проходящей через две параллельные прямые

, .

1073. Доказать, что уравнение плоскости, проходящей через две параллельные прямые

х = а₁ + lt, y = b₁+ mt, z = c_l+nt

и

х = a₂ + lt, у = b₂ + mt, z = с₂ + nt,

может быть представлено в следующем виде:

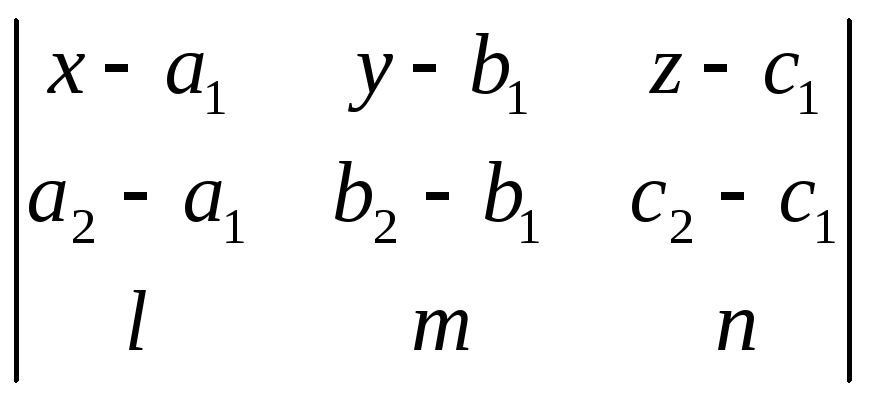=0

1074. Найти проекцию точки С(3; —4; —2) на плоскость, про­ходящую через параллельные прямые

, .

1075. Найти точку Q, симметричную точке Р(3; —4; —6) относительно плоскости, проходящей через М₁ (—6; 1; —5), М₂ (7; —2; —1) и М₁ (10; —7; 1).

1076. Найти точку Q, симметричную точке Р(—3; 2; 5) отно­сительно плоскости, проходящей через прямые

---

1077. Составить уравнение плоскости, проходящей через прямую

х=3t+1, у = 2t + 3, z = —t —2

параллельно прямой

1078. Доказать, что уравнение плоскости, проходящей через прямую

параллельно прямой

x = x₀ +lt, у = y₀ +mt, z =z₀ + nt,

может быть представлено в следующем виде:

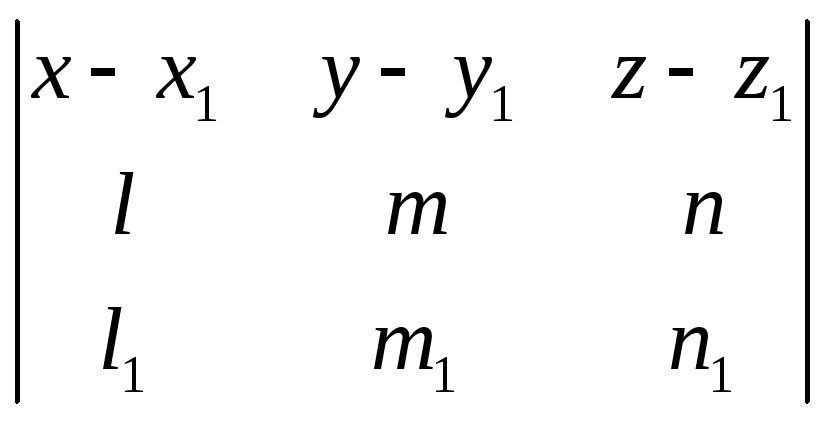=0

1079. Составить уравнение плоскости, проходящей через прямую

перпендикулярно к плоскости Зх + 2у — z — 5 = 0.

1080. Доказать, что уравнение плоскости, проходящей через прямую

x = x₀ +lt, у = y₀ +mt, z =z₀ + nt,

перпендикулярно к плоскости

Ах + Ву + Сz +D = 0

может быть представлено в следующем виде:

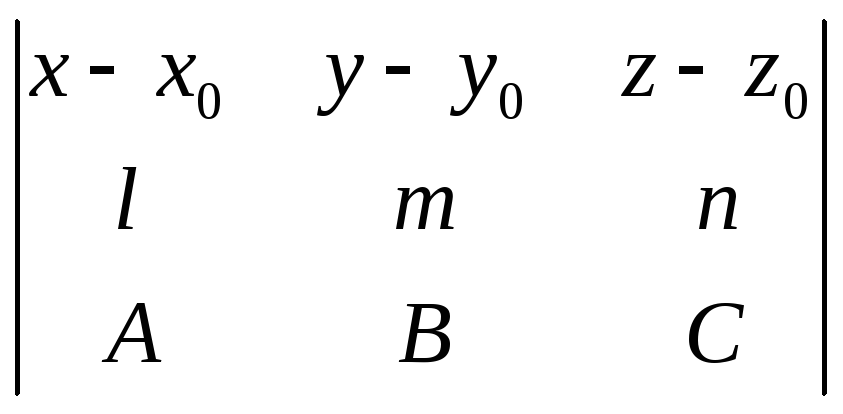=0

1081. Составить канонические уравнения прямой, которая про­ходит через точку М₀(3; —2; —4) параллельно плоскости

Зх — 2у — 3z — 7 = 0

и пересекает прямую

1082. Составить параметрические уравнения прямой, которая проходит параллельно плоскостям

Зх+12у — Зz — 5 = 0, Зх — 4у + 9z + 7 = 0

и пересекает прямые

;

1083. Вычислить кратчайшее расстояние между двумя прямыми в каждом из следующих случаев:

1) ;

2) х=2t — 4; y= — t+4;, z= — 2t- 1

х=- 4t — 5; y= — 3t+5; z= — 5t+5

---

Смотрите также файлы

• kletenik_42.doc

• kletenik_41.doc

• kletenik_40.doc

• kletenik_39.doc

• kletenik_38.doc