§ 1. Определители второго порядка и система двух уравнений

первой степени с двумя неизвестными

Пусть дана квадратная таблица из четырёх чисел a₁, a ₂ , b₁, b ₂ ,

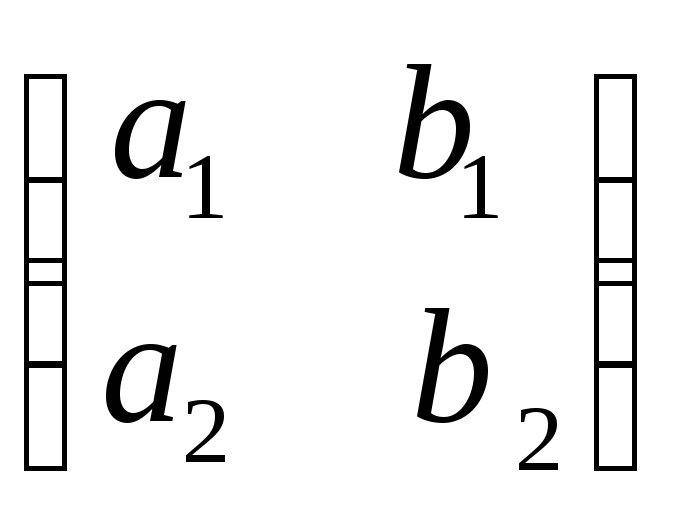. (1)

Число a₁, b ₂ , a₂, b ₁ , называется определителем второго порядка, соответствую-

щим таблице (1). Этот определитель обозначается символом

соответственно имеем:

= a₁ b₂ - a₂ b₁ , (2)

Числа a₁ b₂ a₂ b₁ , называются элементами определителя. Говорят, что эле­менты a₁ b₂ , лежат на главной диагонали определителя, a_s, b_t — на побоч­ной. Таким образом, определитель второго порядка равен разности между произведениями элементов, лежащих на главной и побочной диагоналях. Например,

= — 3* 4 – (—1) 2 = —10 ,

Рассмотрим систему двух уравнений

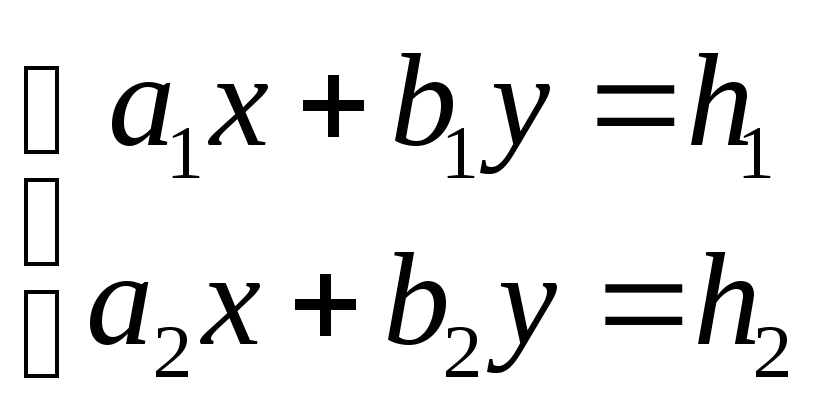(3)

с двумя неизвестными х, у. (Коэффициенты a₁, b₁, а₂, b₂ и свободные члены

h₁, h₂ предположим данными.) Введём обозначения

, , . (4)

Определитель , составленный из коэффициентов при неизвестных системы (3), называется определителем этой системы. Определитель  получается путём замены элементов первого столбца определителя  свободными членами системы (3); определитель  получается из определителя  при помощи за­мены свободными членами системы (3) элементов его второго столбца.

Если   0, то система (3) имеет единственное решение; оно опреде­ляется формулами

---

(5)

Если  = 0 и при этом хотя бы один из определителей _x, _у отличен от нуля, то система (3) совсем не имеет решений (как говорят, уравнения этой системы несовместимы).

Если же  = 0, но также _x = _y = 0, то система (3) имеет бесконечно много решений (в этом случае одно из уравнений системы есть следствие другого).

Пусть в уравнениях системы (3) h₁=h₂ = 0; тогда система (3) будет иметь вид:

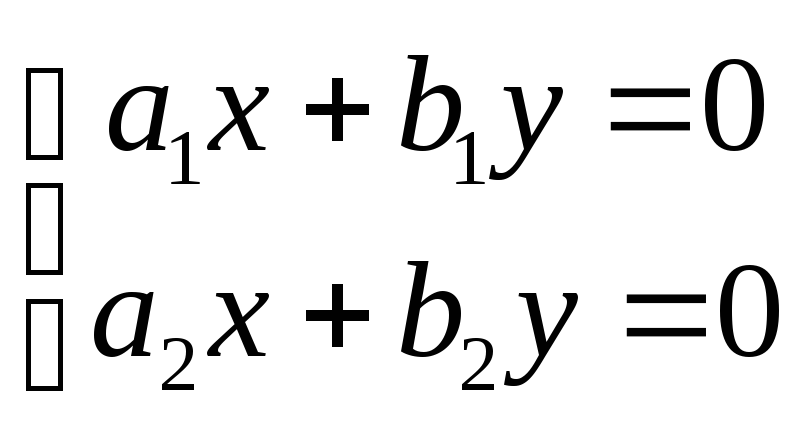(6)

Система уравнений вида (6) называется однородной; она всегда имеет нулевое решение: х = 0, у = 0. Если   0, то это решение является един­ственным; если же  = 0, то система (6), кроме нулевого, имеет бесконечно много других решений.

1204. Вычислить определители:

1) ; 2) ; 3)

4) ; 5) ; 6)

7) ; 8) .

1205. Решить уравнения:

1) ; 2) ;

3) ; 4) ;

5) ; 6)

7) ; 8) .

1206. Решить неравенства:

1) ; 2) ;

---

3) ; 4) ;

1207. Найти все решения каждой из следующих систем урав­нений:

1) 2) 3)

4) 5) 6)

1208. Определить, при каких значениях а и b система уравнений

1) имеет единственное решение; 2) не имеет решений; 3) имеет бесконечно много решений.

1209. Определить, при каком значении а система однородных уравнений

имеет ненулевое решение.

---

Смотрите также файлы

• kletenik_op.doc

• kletenik_o9.doc

• kletenik_o8.doc

• kletenik_o7.doc

• kletenik_o6.doc